构造法在高等数学解题中的应用①
孙梦园
(长治幼儿师范高等专科学校,山西 长治 046000)
0 引 言
所谓构造法,是指在解题过程中使用常规方法按照定向思维难以解决问题时,常常需要依据问题给出的信息,构造一种新的数学形式,如函数,级数,积分等,进而对问题进行转化得到解决的这样一种方法.
构造法作为数学中一种基本且重要的思维方法,它有三个特点:一是在构造的过程中,经常要伴随分析、猜想等思维活动进行;二是构造性思维有时体现在解题的全过程中,也有时体现在关键环节中;三是在构造的“框架”必须在有限的步骤内能实现.运用构造法来解题可以培养学生钻研独创精神及多元化思维,提高他们分析解决问题的能力,下面通过举例来说明几种常见构造方法在高等数学解题中的应用.
1 构造函数
函数在高等数学学习内容中占据很大的比例,而学生对函数也较熟悉,故在用构造法解题时,一个常用的方法是构造函数.构造函数法是指,由问题已知条件的数量关系为对象,构思想象并组合一种新的关系,使问题在新关系下得到转化并解决.运用构造函数解题需要我们具备抽象的构造性思维,并对典型的函数及其特性了然于心。
例1[1]证明:不等式
p>1,n∈N,且n≥2.
分析将欲证的不等式改写为
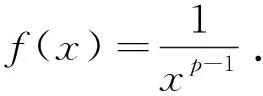
函数f(x)在闭区间[n-1,n](n≥2)连续,在开区间(n-1,n)(n≥2)可导,根据拉格朗日定理[1],则在开区间(n-1,n)内可找到一点n-1+θ,0<θ<1,使得
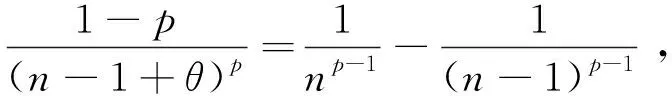
从而
进一步可得
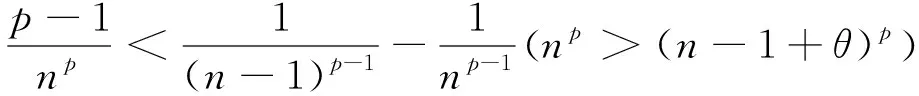
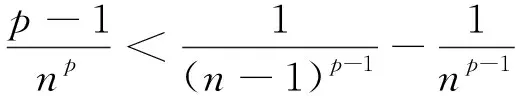
例2[2]已知g(x)在[0,1]上连续,在(0,1)上二阶可导,且g(0)=g(1)=0,求证: 存在ξ∈(0,1)使得2g′(ξ)+ξg″(ξ)=0.
分析根据题设条件,很容易联想到罗尔定理[1],即(0,1)在上至少存在一点η,使得g′(η)=0.如果此时能够构造一个新的函数G(x),其满足罗尔定理条件,则一定存在ξ∈(0,1),使得G′(ξ)=0.若令G′(x)=2g'(x)+xg″(x),此时难以寻找满足条件的G(x).不妨在2g′(ξ)+ξg″(ξ)=0两端同时乘以ξ,得到2ξg′(ξ)+ξ2g″(ξ)=0,这样就可以取函数G(x)=x2g′(x),进而解题.
解构造函数G(x)=x2g′(x).因为g(x)在[0,1]上连续,在(0,1)上二阶可导,且g(0)=g(1)=0,根据罗尔定理,一定存在η∈(0,1),使得g′(η)=0.而G(x)在[0,η]上连续,在(0,η)上可导,且G(0)=G(η)=0,再次利用罗尔定理,一定存在ξ∈(0,η)⊂(0,1),使得G′(ξ)=0,即2ξg′(ξ)+ξ2g″(ξ)=0,进而2g′(ξ)+ξg″(ξ)=0,命题得证.
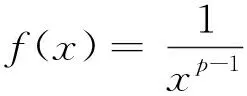
2 构造级数
级数与积分、函数等诸多知识密切联系。构造级数法是指根据条件中的数量关系及结构特征,构造出一个级数, 之后根据级数的理论使问题在新关系下达到转化而解决。

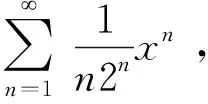


由幂级数可逐项求导,有
x∈(-2,2).

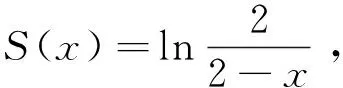
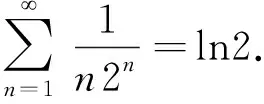
例4[3]数列{xn}的定义如下:x1=n,x2=


…,
…
故
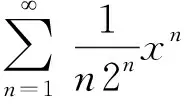
3 构造不等式
针对某些关于数列极限的问题,往往要用到夹逼定理[1],其关键步骤就是构造相应的不等式,然后再取极限来解题.
例5求极限
解对任意的自然数k(k=1,2,3,…,n),有
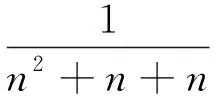
从而


因为
由夹逼定理得

通过构造不等式,转换了解题的方向,从而为原问题解决找到最佳途径.
4 构造积分
根据题目已有的条件,合理的构造积分,再利用积分的性质来求解.
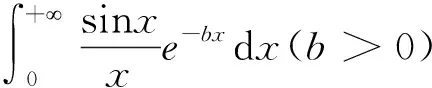


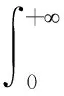
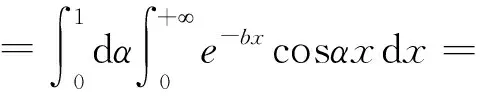


-2π(0-1)=2π
又因为

例6、例7就是通过构造积分,再利用积分性质简化计算,从而避免繁冗复杂的计算过程.
5 构造反例
反例,顾名思义就是指符合命题中条件但不符合结论的例子.通常要说明一个命题是假命题,我们往往会选择特殊值或极端情形来揭露判断的虚假性,这个构造过程就叫做构造反例.
例8[2]判断下面命题是真命题还是假命题:
(1) 若函数|g(x)|在[m,n]可积,则g(x)在[m,n]也可积.
(2) 若函数g2(x)在[m,n]可积,则g(x)在[m,n]也可积.
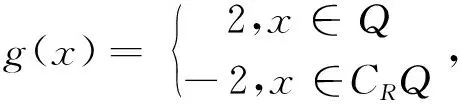
例9[5]判断下面命题是否正确。
(1)如果数列{an}的子数列{a2n}、{a2n+1}都收敛,则其一定收敛;
(2)如果数列{an}收敛,则数列{|an|}也收敛,反之依然成立.
解对于命题(1),可以构造数列2,1,2,1,2,1,…,其子数列{a2n},{a2n+1}都收敛,但是{an}却不收敛,故命题(1)错误.
对于命题(2),数列{|(-2)n|}是收敛的,但数列{(-2)n}却不收敛,故命题(2)也是错误的.
遇到判断命题真假的问题时,如果我们无法正面去证明命题真假,这时就可以考虑构造反例来解题.
6 构造矛盾
构造矛盾方法,是指否定原命题的结论,之后利用否定的命题找出一个能指出其错误的数学对象,从而引发矛盾,使原命题得以证明.
例10[5]证明方程x3-6x+c=0在[0,1]内不可能存在两个不相等的实数根.
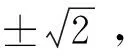
例10在采用构造矛盾法的同时用到了构造函数法,可见在解题过程中构造方法灵活多样,要从多角度进行思考.
通过以上的探讨,可以发现,在高等数学中构造法是一种非常巧妙的方法,其方法带有猜测性、试探性,思维极具创造性.构造法解决问题的关键在于“构造”,“构造”怎样的辅助元素,没有固定通用的方法,所构造的数学模型也是灵活多变的.
7 结 论
该文从六种“构造模式”: 构造函数、构造级数、构造不等式、构造积分、构造反例、构造矛盾入手,展示了构造法的简化功能及其技巧性、创造性.构造思想需要长期经验积累,才能灵活运用.使用构造法解题不仅体现了数学中发现、类比思想,同时渗透着联想、猜想、特殊化等重要的方法.学生学会了构造法,就可以在欣赏数学之美的同时还可以感受到解题乐趣,更重要的是可以开拓思维空间,提高解题的能力,有利于创新能力的培养.

