基于综合算法的随机潮流计算方法

孟代江 张淑荣

同济大学 电子与信息工程学院 上海 201804

1 研究背景

随着风能和太阳能等清洁能源在电力系统中发电占比快速增长,影响电力系统运行状态的不确定性大大增加,电力系统稳定运行面临着更大的挑战。随机潮流计算能够在系统各节点功率注入,系统参数具有不确定性条件下,获得电压和相角等系统状态量信息的概率分布,是解决电力系统不确定性这一难题的有效方法。随机潮流计算方法的研究近年来受到广泛关注。

目前,随机潮流的计算方法主要有模拟法、解析法、代理模型类方法。

模拟法[1-4]只要保证足够的采样次数,即可达到很高的精度,通常作为其它方法的基准方法,但收敛速度较慢。

解析法包括半不变量法[5-6]、点估计法[7-8]等,不需要抽样,通过对原函数的局部线性化或利用某些特征量的性质,直接求取输出变量的期望和方差,虽然计算效率高,但是精度较低,适用范围有限。

随机潮流问题的原函数通常是隐含在复杂非线性潮流方程中的隐函数,求解速度相对较慢。对此,代理模型类方法用某种特定结构的正交多项式逼近函数,构造随机潮流模型的代理模型,进而基于逼近函数进行大量抽样计算,输出变量的概率特征,也可以通过基函数系数直接计算输出变量的期望、方差等概率特征值。代理模型类方法又可以分为随机伽辽金方法和随机配置点法。

随机伽辽金方法用逼近函数代替各输出变量,代入潮流方程,通过正交多项式性质求解方程,获得各基函数系数。这种方法通过选择合理的基函数及展开阶次,可以获得很高的精度,但是基函数项由于随机输入维数的增加而迅速增加,方程也更加复杂,不适用高维系统的求解[9-10]。

随机配置点法可以分为伪谱类方法和插值类方法。伪谱类方法基于数值积分及二次方逼近理论,能够精确计算任意项基函数系数,但是由于基函数项数随维度指数的上升而会导致产生维数灾难。文献[11-12]提出自适应稀疏伪谱法,在基函数项扩展时,优先扩展对于提高精度作用大的基函数项,大幅减少基函数项的数量。文献[13]提出更精确的逼近误差估计,提高计算精度,并提出多输出同时扩展计算的策略。以上文献虽然在一定程度上改善了维数灾难问题,但是并未根本解决,在高维场景中仍无法高效率应用。

文献[14-16]提出一种插值型方法——低阶多项式逼近法,通过构造由若干阶次的低次多维正交多项式基函数的线性组合来逼近原函数,通过交替最小二乘法逐维求解基函数系数。这一方法的基函数项数与随机输入变量维数呈现线性关系,即所需抽样点与输入维数呈线性增长关系,避免维数灾难问题,但在低维时的计算精度与自适应稀疏伪谱法相差甚远。

笔者针对代理模型类方法展开研究,分析自适应稀疏伪谱法和低阶多项式逼近法的计算时间复杂度,基于两种方法的优势提出一种基于综合算法的随机潮流计算方法。这一方法在低、中、高维度场景中都有较高的计算精度和计算效率,通过算例验证了这一方法的有效性和可行性。

2 随机潮流数学模型

随机潮流模型可以简写为:

U=f(W)

(1)

U=(U1,U2,…,UD)

W=(W1,W2,…,Wd)

式中:U为节点电压、相角等系统状态随机变量;D为输出随机变量数量;W为风光电场出力及负荷等输入随机变量;d为输入随机变量数量;f表示潮流方程隐含的关于系统状态与节点注入功率的隐函数关系。

考虑风光出力的不确定性通常直接由风速、光照强度等因素决定,随机潮流模型又可以写为:

U=f(v,r,PL)

(2)

式中:v为各风电场的风速向量,一般认为服从韦布尔分布;r为各光伏场的光照强度向量,一般认为服从贝塔分布;PL为各节点负载有功功率,一般认为服从正态分布。

3 自适应稀疏伪谱法计算时间复杂度

对于随机潮流模型,自适应稀疏伪谱法构造的单输出多项式逼近函数为:

(3)

(4)

式中:Qk(〈φn,f〉)为待计算的高斯积分;φn为正交基函数;ck为网格系数。

自适应稀疏伪谱法的计算时间主要花费在对原函数的抽样上,对自适应稀疏伪谱法计算时间复杂度进行分析,主要取决于自适应稀疏伪谱法积分点数量的分析。

K={k:d≤k1+k2+...+kd≤l+d}

(5)

这一形式的指标集包含了所有总阶次不超过l的正交基函数。文献[17]简单推导了当阶次l为0～7时指标集所需总积分点数n与输入随机变量维数d的函数关系,见表1。

表1 总积分点数与输入维数关系

根据文献[18],对于随机潮流问题,当阶次l为3时,使用经典Smolyak指标集的稀疏伪谱法即达到最高逼近精度。继续增大l,稀疏伪谱法的逼近精度几乎不变。

由此,可以估算基于自适应稀疏伪谱法的随机潮流计算时间复杂度为O(Dd3),输出随机变量数量一般是输入随机变量数量的一到两倍,即D为cd,c为1～2。综合以上分析,自适应稀疏伪谱法的随机潮流计算时间复杂度为O(cd4)。

另外,对于随机潮流问题,通常认为10 000点拉丁超立方法可以获得随机潮流输出变量各阶矩的精确值。根据自适应稀疏伪谱法所需采样点数量与基函数阶次、输入维度的关系,以及基准拉丁超立方法所需采样点数,采取如下策略获得高维问题和低维问题的分界值。由于自适应稀疏伪谱法的指标集形式灵活,指标集可以位于阶次为2和阶次为3的经典指标集之间。考虑到反映潮流方程的非线性特性,基函数总次数一般需大于2。由此,根据表1,并令自适应稀疏伪谱法的积分点数下限2d2+2d+1的值为10 000,可求得输入维数为70.2。据此,可认为输入维数不小于70时属于高维输入情况,此时自适应稀疏伪谱法计算效率低于拉丁超立方法,应采用无维数灾难的求解方法求解随机潮流。反之,输入维数小于70时属于低维输入情况,此时自适应稀疏伪谱法的计算效率可能更高,且由于自适应稀疏伪谱法计算精度上限较低阶多项式逼近法更高,可尝试先使用自适应稀疏伪谱法进行随机潮流求解,若计算精度不满足要求,则再转向低阶多项式逼近法或拉丁超立方法进行求解。

4 低阶多项式逼近法计算时间复杂度

低阶多项式逼近法构建的单输出逼近函数表达式为:

(6)

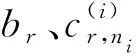
低阶多项式逼近法的计算分为两部分,一部分是对原函数的抽样,另一部分是采用交替最小二乘算法求解基函数系数。假设抽样一次的时间为teval,则抽样时间tsample为Nteval,N为抽样次数。低阶多项式逼近法采用交替最小二乘方法求解基函数系数的过程还可以细分为三部分。

(1) 计算冻结系数,这部分的总计算时间tci为:

tci=DrmaxdN(d-1)(pmax+1)tbasis

(7)

(2) 计算最小二乘,这部分的总计算时间t1s为:

t1s=Drmaxdtsolve

(8)

(3) 计算收敛判据,这部分的总计算时间tErr为:

tErr=DrmaxNd(pmax+1)tbasis

(9)

式中:tbasis为计算一个单维正交基函数在一个点处的值所需要的计算时间;tsolve为求解一次最小二乘问题所需要的时间。

主要计算时间还是在最小二乘计算上,rmax一般取3～10,输出随机变量数量一般是输入随机变量数量的一到两倍,因此低阶多项式逼近法的随机潮流计算复杂度约为O(d2)。

5 基于综合算法的随机潮流计算过程

基于综合算法的随机潮流计算步骤如下。

(1) 给定随机潮流系统函数X=f(W),若d<70,进行步骤(2);反之,进行步骤(4)。

(2) 设定最大抽样次数Nmax,误差收敛阈值为TOL。

(3) 采用自适应稀疏伪谱法求解随机潮流。若全局误差η满足小于TOL,且抽样次数N满足小于Nmax,则进行步骤(8);反之,进行步骤(4)。

(4) 比较低阶多项式逼近法估计计算时间t1和t2,若t1≤t2,则进行步骤(5);反之,进行步骤(7)。t1、t2分别为:

+Nsteval

(10)

t2=Nmaxteval

(11)

D0、rmax,0、d0、Ns,0、d0-1、pmax,0是基准问题参数,tci,0为对应组参数的tci,这些参数由已知系统先行计算得出,以便在计算t1、t2时更加快捷。

(5) 设定抽样次数Ns为drmax(pmax+1)2,使用低阶多项式逼近法求解随机潮流,计算低阶多项式逼近法逼近误差ε。

(6) 若ε小于3TOL,则进行步骤(8);反之,进行步骤(7)。

(7) 使用Nmax点拉丁超立方法求解随机潮流。

(8) 输出电压幅值、相角的期望和标准差。

基于综合算法的随机潮流计算流程如图1所示。

6 算例

通过调整设置不同规模大小的系统和随机输入变量数量,检验综合算法的逼近精度和计算时间,以及验证方法的有效性和优越性。所采用系统参数全部来自Matpower 6.0。

6.1 算例1 IEEE-30节点系统

在IEEE-30节点系统基础上,添加五个服从韦布尔分布的风电功率注入和四个服从贝塔分布的光伏注入。其中,五个风电场分别配置在1、5、6、9、10节点处,参数λ为8,k为3,切入风速为2 m/s,额定风速为12 m/s,切出风速为25 m/s,功率因数为0.2,额定功率为100 MW。四个光伏电场分别配置在12、13、14、15节点处,参数α、β为2.222 2,光照强度峰值为1 000 W/m2,光伏电场辐射点辐射为150 W/m2,标准太阳辐射为1 000 W/m2,额定功率为50 MW。自适应稀疏伪谱法设置最大抽样次数为10 000次,误差收敛阈值为0.005。以10 000点拉丁超立方法计算结果为基准。

这一随机潮流问题的输入随机变量维数为9,可以认为是低维问题。采用基于综合算法求解这一问题时,使用了自适应稀疏伪谱法。其中,总积分点数为229,计算时间为0.175 s,总指标数为60,误差估计为0.004 189。由于误差估计小于给定误差收敛阈值0.05,因此采用自适应稀疏伪谱法的计算结果作为最终输出结果。计算结果输出期望对比如图2所示,输出标准差对比如图3所示。基准拉丁超立方法计算时间为3.596 s。

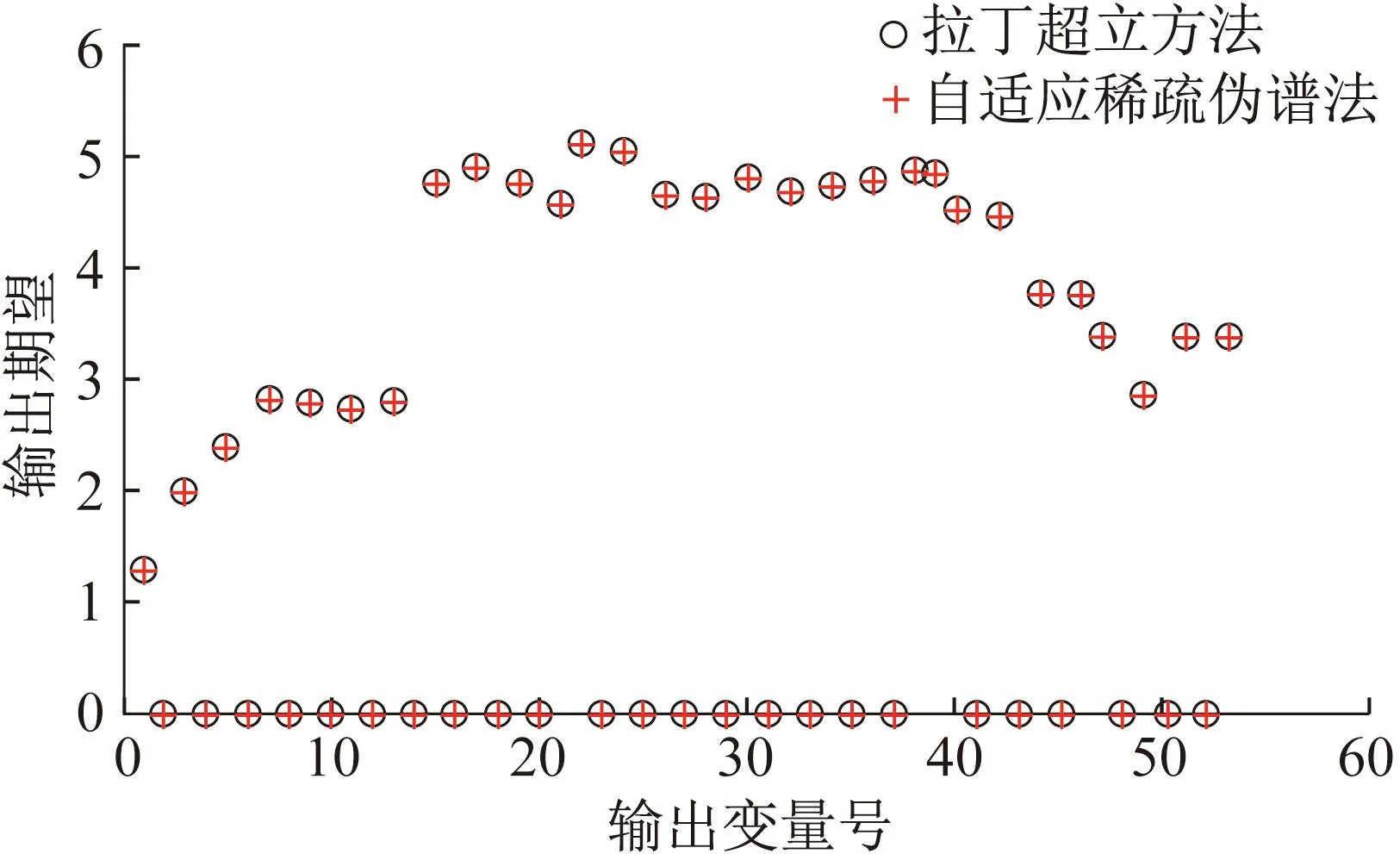
图2 算例1输出期望对比

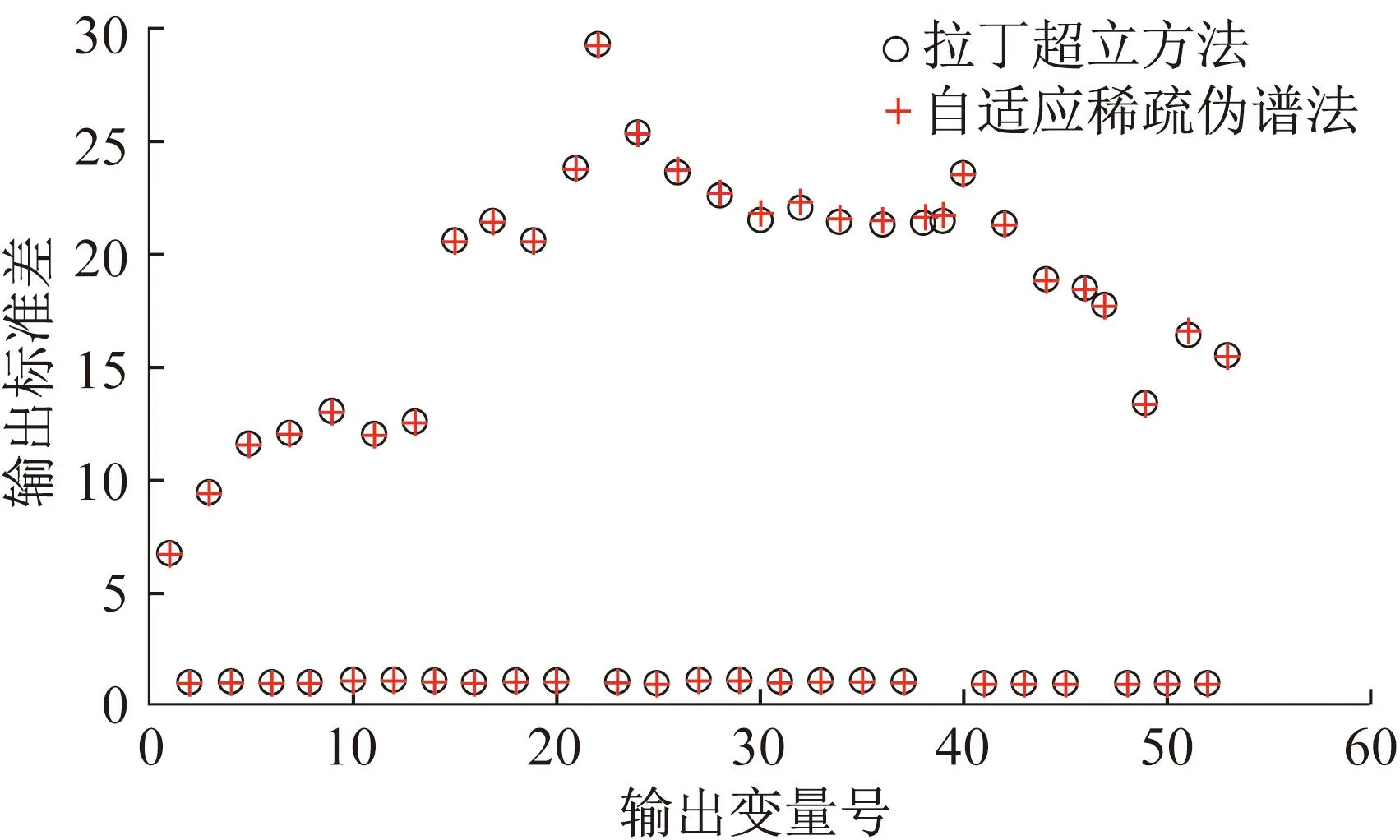
图3 算例1输出标准差对比

由图2和图3可以看出,自适应稀疏伪谱法对系统各输出变量的计算结果几乎与拉丁超立方法计算结果重合,说明自适应稀疏伪谱法对于低维场景具有很高的精度。

由于低阶多项式逼近法和拉丁超立方法的采样点数量与自适应稀疏伪谱法每次计算时按需所得不同,而是先验给定的,因此为了体现笔者所提方法在求解问题时的有效性,做出采样次数为200、230、260时的低阶多项式逼近法和拉丁超立方法实际逼近误差曲线,实际逼近误差用各输出变量的标准差相对于拉丁超立方法计算出的基准值的平均相对误差来衡量,比较结果如图4。

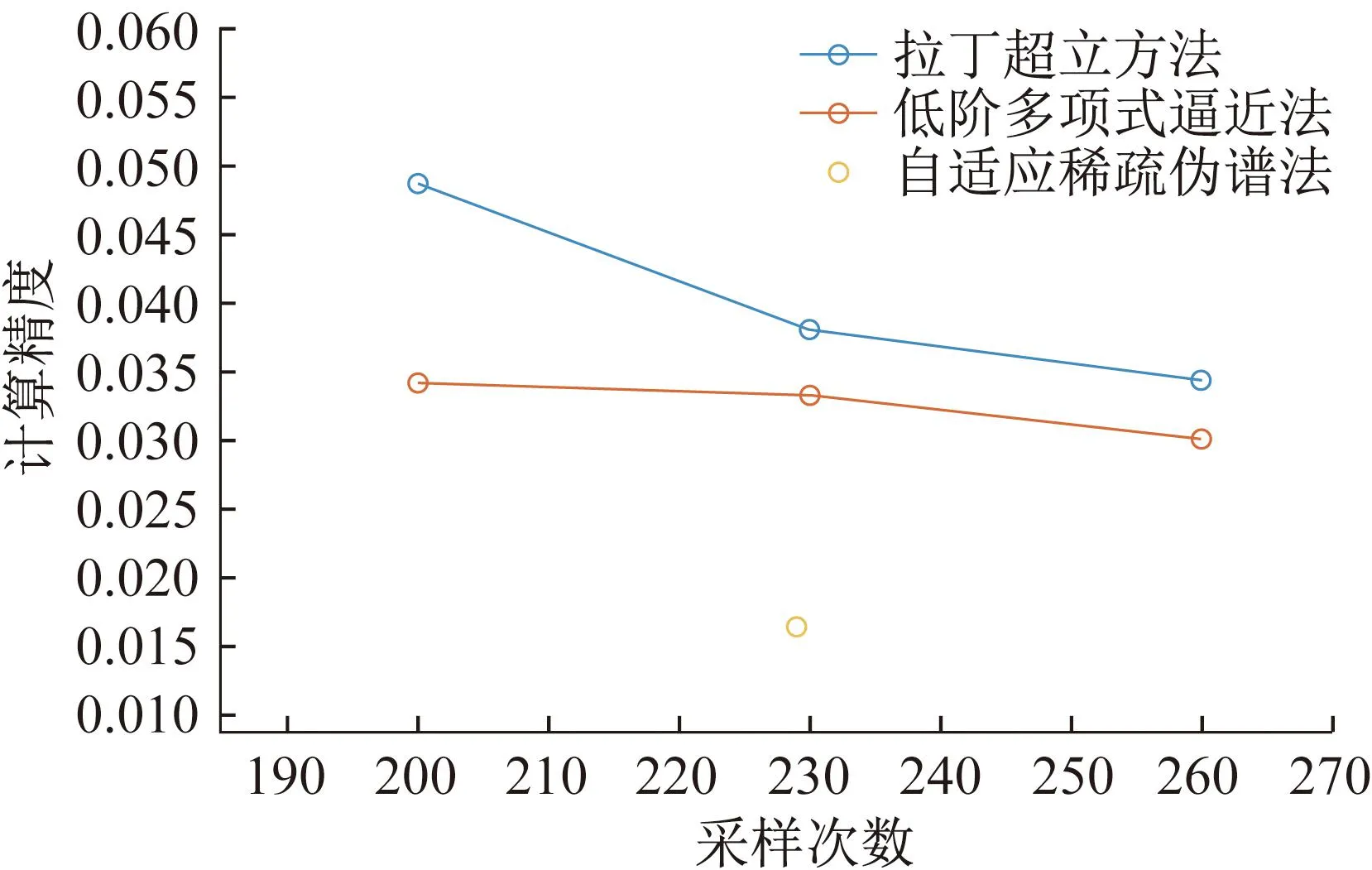
图4 算例1采样次数对比

拉丁超立方法的运行时间分别为0.121 s、0.133 s、0.135 s,低阶多项式逼近法的运行时间分别为0.319 s、0.322 s、0.354 s。无论是低阶多项式逼近法、自适应稀疏伪谱法,还是拉丁超立方法,计算时间都极短,采用计算精度最高的方法对随机潮流进行求解,无疑是最优的选择,因此从算例1可以看出,综合算法充分利用了自适应稀疏伪谱法在低维时的高计算精度,展现了方法的有效性。

6.2 算例2 IEEE-85节点系统

在IEEE-85节点系统的基础上,添加三个服从韦布尔分布的风电注入、八个服从贝塔分布的光伏注入、59个服从高斯分布的负荷噪声,风电场位于1、2、3节点处,光伏电场位于4、5、6、7、10、11、14、15节点处。有84个负荷噪声在其它节点处,均值为原负荷量,标准差为5%均值。风光电场参数及自适应稀疏伪谱法参数同算例1。

此时,输入维度为70,属于中高维问题。综合算法在求解这一问题时,先采用自适应稀疏伪谱法进行求解,然后采用10 000点拉丁超立方法进行求解。自适应稀疏伪谱法的求解结果为采样次数10 025、指标数1 906、全局误差指示器0.125 01,计算时间19.675 s。拉丁超立方法与自适应稀疏伪谱法计算结果输出标准差对比如图5所示。采用拉丁超立方法进行这一系统随机潮流的求解,精度远远高于自适应稀疏伪谱法。因此,笔者所提方法可以在很大程度上保证对各种规模系统随机潮流求解的精度和计算时间。

图5 算例2拉丁超立方法与自适应稀疏伪谱法输出标准差对比

综合算法在求解这一问题时,首先采用自适应稀疏伪谱法进行求解,在求解精度不能满足要求时,进而判断低阶多项式逼近法与拉丁超立方法的计算时间,选择时间较短的进行计算。根据自适应稀疏伪谱法的抽样时间和抽样点数,可以计算出单次采样时间为1.097 9×10-3s。再根据已知系统计算tbasis为4.916 5×10-8s。设置低阶多项式逼近法采样点数为1 000。计算出低阶多项式逼近法预计所需时间为75 s,而拉丁超立方法预计所需时间为10.9 s。可见,综合算法最终采用拉丁超立方法进行计算。

综合算法与低阶多项式逼近法计算结果输出标准差对比如图6所示,可以看出此时低阶多项式逼近法与综合算法精度近似,采取综合算法计算时间更短,充分体现综合算法的合理性和有效性。

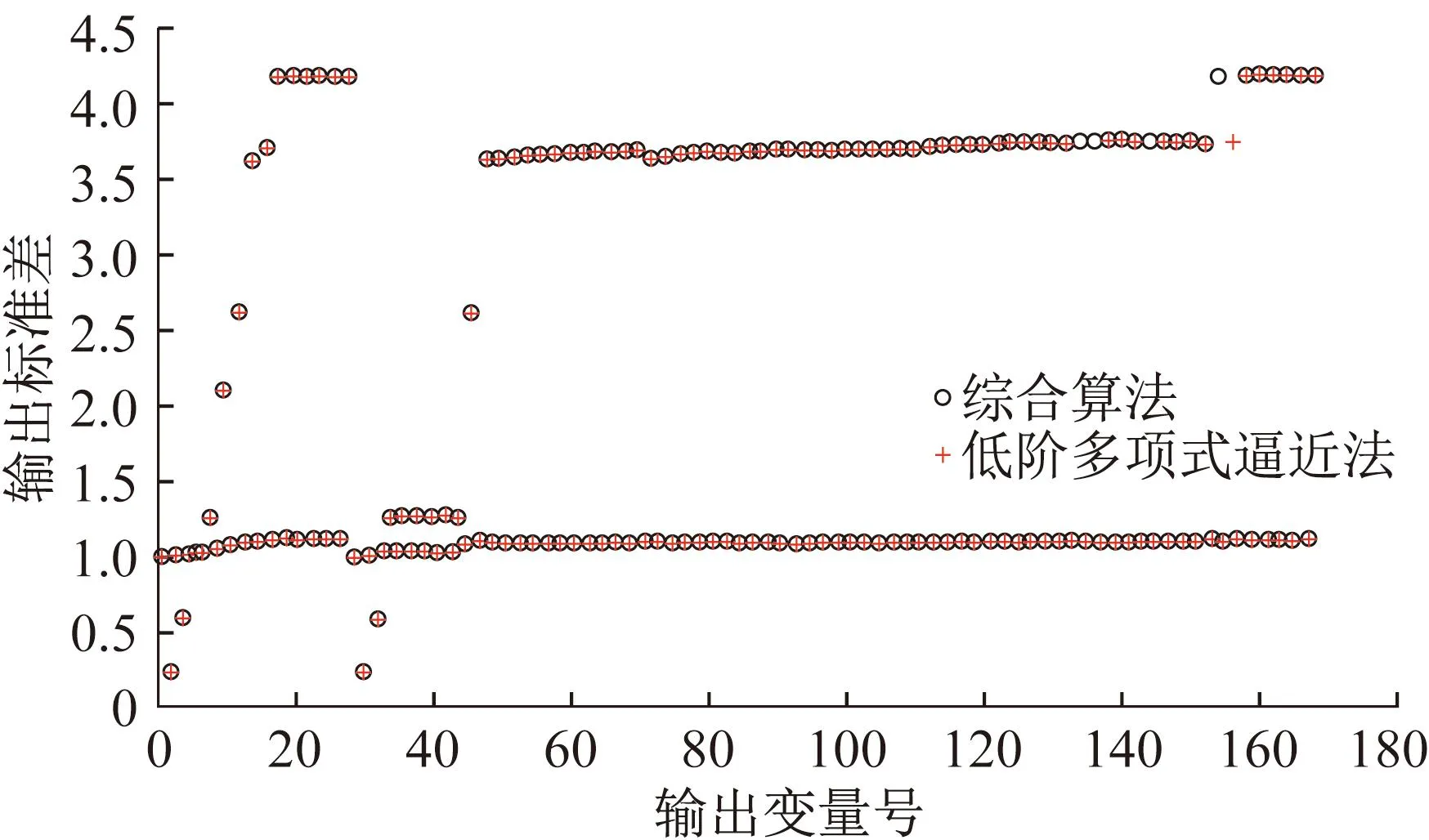
图6 算例2综合算法与低阶多项式逼近法输出标准差对比

7 结束语

基于综合算法的随机潮流计算方法在随机潮流问题求解的过程中,充分结合了三种各具优势的随机潮流计算方法,并且通过计算精度、计算时间等条件,将三种方法衔接,发挥三种方法的长处,极大避免自适应稀疏伪谱法在高维计算量时的维数灾难问题。通过算例,验证了所提方法的有效性。