A Logic for Probabilities of Successive Events*

Yanjun Li Jiajie Zhao

Abstract. In the set language of probability theory,besides complement,intersection,and union,there is another important operation: product.The product of two basic events expresses that these events occur in succession.However,there is limited research about successive events in the literature on probability logic.In this paper,we propose a modal logic(called DML)to capture the reasoning about successive events in probability theory,and then we construct a probability logic (called PLDML) based on DML.We compare DML with standard modal logic on Kripke semantics and show that DML is equivalent to the normal modal logic on deterministic models.We also give a deductive system of PLDML and show its completeness.

1 Introduction

In probability theory,an event is expressed by a set.In the literature on logic for probabilities,the basic events and their Boolean combinations are well-studied.For example,the negation of an event A means that A does not happen.The conjunction of two events A and B means both A and B happen.The disjunction of two events A and B means that either A or B happens.However,successive events cannot be expressed by Boolean operators.In set language,successive events can be expressed by the product of basic events.

Successive events are several events occurring in succession.It is worth pointing out that events occurring in succession might occur at the same time.Succession here is to indicate order not time.Consider the example of tossing a die,and we assume that all dies are fair.There are 6 possible results.The die might fall with 1,2,3,4,5,or 6 up.LetEbe the event that the die falls with an even number up,that is,

The probability ofEeis.LetE>3be the event that the die falls with a number bigger than 3 up,that is,

The probability ofE>3is.Now if two persons respectively toss a die at the same time,the result that the first die falls with an even number up and the second die falls with a number bigger than 3 up is successive events,which is represented by

The probability ofEe×E>3is the product of the probability ofEeand the probability ofE>3,namely

The research on logic for probabilities can date back to Fagin et al.([2,3]).They propose a probability logic where linear inequalities involving probabilities are allowed.For example,a typical formula ”w(φ) -2w(ψ)≥0” (or equivalentlyw(φ)≥2w(ψ))means that” the probability ofφis at least twice the probability ofψ”.The deductive system of the probability logic given by[2,3]is an extension of both propositional logic and linear inequality logic with some probability axioms and rules.The deductive system is weakly complete.

Another way of formalizing probability is to interpret modal operators of modal logic as probability(see[4,6,7]).A modal formulaφmeans that the probability ofφis strictly greater thanr.In the model,the probability function assigns each measurable set a number in a base,where a base is a finite subset of the set[0,1]that satisfies some conditions.Due to the fact that the base is finite,this probability has the property of compactness,and it also has strong completeness.

Zhou ([16,17]) proposes a probability logic which is an extension of propositional logic with probability operators.A formulaLrφmeans that the probability ofφis no less thanr,whereris a rational number between 0 and 1.The deductive system of this probability logic is an extension of propositional logic with some probability axioms and rules.One of these probability rules is aω-rule,which has an infinite number of premises and one conclusion.Zhou shows the weak completeness and confirms a conjecture of Larry Moss that the infinitary rule can be replaced by a finitary rule.

Different from [16,17],Ognjanović et al.(see [10,11,12,13]) proposes a probability logic with not onlyω-rule but also infinitary derivations.A derivation(or a proof) in Ognjanović’s system is a well-founded tree in which some nodes might have an infinite number of successors(see[9]).Based on infinitary derivations,this probability logic is shown to have strong completeness.

None of the papers mentioned above considers the probability of successive events in their logical language.In this paper,we propose a modal logic for reasoning about successive events and construct a probability logic based on it.The main contributions are listed as follows:

· We consider a fragment of the language of linear temporal logic,in which successive events can be expressed.

· We propose a semantics that combines the semantics of linear temporal logic(see[15])and the update semantics of public announcement logic(see[5,14]).

· We compare this semantics with standard Kripke semantics.

· We construct a probability logic based on this logic and give a complete deductive system.

The paper is organized as follows.Section 2 introduces the modal logic DML to capture the reasoning about successive events.Section 3 gives the alternative Kripke semantics of DML.Section 4 proposes a probability logic based on DML and gives a deductive system PLDML.Section 5 shows the weak completeness of PLDML.Section 6 concludes with some remarks.

2 A Modal Logic for Sequential Events

In this section,we introduce the logic,called DML(Deterministic Modal Logic),to capture the reasoning about successive events in probability theory.

Let P be a set of propositional letters.

Definition 1(Language of DML).The language of DML,denoted byLDML,is defined by the following BNF(wherep ∈P):

The auxiliary connectives⊥,,∨are defined as abbreviations as usual.

The formula○φmeans that the eventφwill happen in the next step.What is more,the formulaφ ∧○nψwherenis the modal depth ofφmeans that the eventsφandψsuccessively happen.We use(φ;ψ)to denote the formulaφ ∧○ψ.

The languageLDMLis a fragment of linear temporal logic without theuntilmodalityU.

Definition 2(Model of DML).A DML-model(or simply a model)is a tripleM=〈S,Ω,V〉where

·Sis a non-empty set of states;

· Ω⊆S∗is a non-empty set of sequences overSthat is prefix-free;

·V: P2Sis a valuation that labels each propositional letter with a set of states.

For eachρ ∈Ω,(M,ρ)is called a pointed model.

Intuitively,eachs ∈Sstands for a basic event,and eachρ ∈Ω stands for a sequence of successive events.Please note that Ω is a subset ofS∗.This means that only some successive events are allowed,which is in line with practice.For example,in sampling without replacement,only some basic events(not all possible basic events)can occur in succession.

The length of the sequenceρis denoted as|ρ|.Then-th character of the sequenceρis denoted asρ[n].The suffix ofρstarting at thei-th character is denoted asρi.For example,letρ=s1s2s3s4.We then have that|ρ|=4,ρ[1]=s1,andρ3=s3s4.

Given a modelM=〈S,Ω,V〉,we useM-nto denote the model〈S,Ω-n,V〉where Ω-n={ρn+1|ρ ∈Ω}.It is obvious that(M-n)-m=M-(n+m).What is more,we use[ρ]M(or simply[ρ])to denote the set{σ ∈Ω|ρis a prefix ofσ}.

The intuition of the updated modelM-nis that after moving forwardnsteps,we will only consider the sequence of successive events that could be generated from this moment.In spirit,it is similar to the update model in public announcement logic.

Definition 3(Semantics of DML).

We use〚φ〛M(or simply〚φ〛)to denote the set{ρ|M,ρ⊨φ}.

This semantics is different from the semantics of linear temporal logic.The key feature of this semantics is that a formula captures to a set of sequences of successive events.This makes DML to be a natural generalization of propositional logic for basic events,where a propositional formula corresponds to a set of basic events.This feature can be illustrated more clearly by the following examples.

Example 1(Sampling with replacement).Imagine there is an opaque box,containing 4 red balls(R)and 1 black ball(B).You draw one ball from the box per time with a replacement.Now consider the case you draw from the box twice,which can be depicted by Figure 1.

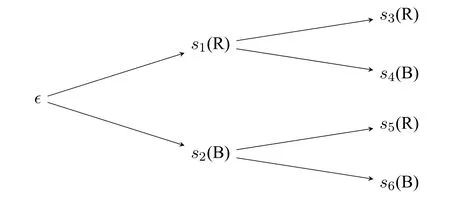
Figure 1: Sampling with replacement

Let the propositional letterpRdenote “draw a red ball”,and letpBdenote “draw a black ball”.So we can construct the modelM=〈S,Ω,V〉as follows:

·S={s1,s2,s3,s4,s5,s6},

· Ω={s1s3,s1s4,s2s5,s2s6},

·V(pR)={s1,s3,s5},andV(pB)={s2,s4,s6}.

The formulapRrepresents the event that draws a red ball at the first time.By the semantics of DML,we get that〚pR〛={s1s3,s1s4}={[s1]}.

The formula○pRrepresents the event that draws a red ball at the second time.By the semantics of DML,we get that〚○pR〛={s1s3,s2s5}.

The formulapR;pBrepresents the successive events that firstly draw a red ball and secondly draw a black ball.By the semantics of DML,we get that〚pR;pB〛={s1s3}.

In the remainder of this section,we will consider two operations on models:generated submodel and disjoint union.These two operations will play important roles in the proof in Section 5.

Definition 4(Generated submodel).GivenM= 〈S,Ω,V〉andρ ∈Ω,the modelM|ρ=〈S′,Ω′,V′〉is defined as follows:

·S′={s ∈S|soccurs inρ};

· Ω′={ρ};

·s ∈V′(p)if and only ifs ∈V(p).

To show that the generated submodel preserves the truth of formulas,we will need the following proposition which can be easily checked.

Proposition 1.Given two models M1= 〈S1,Ω1,V1〉and M2= 〈S2,Ω2,V2〉,we have that M1,ρ⊨φ if and only if M2,ρ⊨φ if the following conditions are satisfied:

·ρ ∈Ω1∩Ω2

·s ∈V1(p)if and only if s ∈V2(p)for each s occurs in ρ and each p.

Proposition 2.For each formula φ ∈LDML,we have that M,ρ⊨φ if and only if M|ρ,ρ⊨φ.

Proof.It can be proved by induction onφ.The base step and Boolean cases are straightforward.We will only consider the case thatφis of the form○ψ.

Left-to-right:Assume thatM,ρ⊨○ψ.This means|ρ| >1 andM-1,ρ2⊨ψ.By inductive hypothesis,(M-1)|ρ2,ρ2⊨ψ.Then by proposition 1,we can get(M|ρ)-1,ρ2⊨ψ.By the semantics,we then have thatM|ρ,ρ⊨○ψ.

Right-to-left:AssumeM|ρ,ρ⊨○ψ.This means|ρ|>1 and(M|ρ)-1,ρ2⊨ψ.Then by proposition 1,we can get(M-1)|ρ2,ρ2⊨ψ.By inductive hypothesis,M-1,ρ2⊨ψ.By the semantics,we then have thatM,ρ⊨○ψ.□

Definition 5(Disjoint union).Let{M1,··· ,Mn}be a finite set of models such that there is no common state between each two of them.The model=〈S′,Ω′,V′〉is defined as follows:

·s ∈V′(p)if and only ifs ∈Vj(p)wheresis a state ofMj.

Proposition 3.Given a finite set of models,{M1,··· ,Mn},for each formula φ ∈LDML,we have that Mi,ρ⊨φ if and only if,ρ⊨φ where1≤i ≤n.

Proof.It can be proved by induction onφ.We will only consider the case thatφis of the form○ψ.

Left-to-right:Assume thatMi,ρ⊨○ψ.This means|ρ| >1 and,ρ2⊨ψ.By the inductive hypothesis,,ρ2⊨ψ.Thus it follows by the semantics that,ρ⊨○ψ.

3 Kripke Semantics of LDML

In this section,we consider the standard Kripke semantics of the languageLDML,and show that DML is equivalent to the normal modal logic on the class of deterministic models.

Definition 6(Kripke model).A Kripke model forLDMLis a tripleK= 〈S,R,V〉whereSandVare the same as Definition 2,andRis a deterministic binary relation onS,that is,ifsRtandsRvthent=v.For eachs ∈S,〈K,s〉is called a pointed Kripke model.

From the definition above,it can be seen that in this paper we assume that all Kripke models are deterministic.This is because we only consider deterministic Kripke models in this paper.

Definition 7(Kripke semantics).The Kripke semantics ofLDML,which in this paper is denoted as ⊩,is standard(cf.[1]),where the modal formula○φis interpreted as an existential modal formula:

From the definition above,it can be seen that the interpretation of○φis the same as the existential modal formula(normally denoted as ◇φ)in standard modal logic.So,in this paper,we will abbreviate the formula¬○¬φas□φ.

Given a Kripke modelK= 〈S,R,V〉,a (possibly infinite) sequence of statess1s2··· is called aK-path if and only ifsnRsn+1for alln ≥1.Especially,eachs ∈Sis aK-path.AK-pathρis called a fullK-path if and only if either it is of infinite length orρ=s1···snand there is no sucht ∈SthatsnRt.

The following proposition states that for each Kripke model,there are equivalent DML-models.

Proposition 4.Given a Kripke model K=〈S,R,V〉,for each setΩof full K-paths,we have that〈S,Ω,V〉,ρ⊨φ if and only if K,s⊩φ where ρ[1]=s.

Proof.We prove it by induction onφ.The basic step and Boolean cases are straightforward.Ifφ:=○ψ,there are two cases:|ρ|=1 or|ρ|>1.

For the case of|ρ|=1,by the DML-semantics,we always have that〈S,Ω,V〉,ρ○ψ.Meanwhile,sinceρis a fullK-path and |ρ|=1,this follows that there is no such statetthatsRtinK.Thus,we also always have thatK,s○ψ.

For the case of|ρ|>1,the proof is as follows:

If 〈S,Ω,V〉,ρ⊨○ψ,it follows that 〈S,Ω-1,V〉,ρ2⊨ψ.By the inductive hypothesis,K,s2⊩ψwheres2=ρ[2].Due toρ[1]=s ∈S,we can getsRs2.Then by Kripke semantics,we have thatK,s⊩○ψ.

IfK,s⊩○ψ,it follows that there exists a states2such thatsRs2andK,s2⊩ψ.By the inductive hypothesis,〈S,Ω′,V〉,ρ′⊨ψwhereρ′[1]=s2.By Proposition 1,we then have that〈S,{ρ′},V〉,ρ′⊨ψ.Sinceρ′is a fullK-path starting froms2andsRs2,it follows thatsρ′is also a fullK-path.Then by the DML-semantics,we have that〈S,{sρ′},V〉,sρ′⊨○ψ.□

Next,we will show that for each DML-model,there is an equivalent Kripke model.

Definition 8(M•).Given a DML-modelM= 〈S,Ω,V〉,a Kripke modelM•is defined as〈S•,RΩ,V •〉where

·S•={σ|there existsρ ∈Ω such thatσis a suffix ofρ}.In other words,S•is the suffix-closure of Ω.

·ρR•σif and only ifσ=ρ2.It is obvious thatR•is deterministic.

·σ ∈V •(p)if and only ifσ[1]∈V(p).

Proposition 5.Given aDML-model M,we have that the Kripke model(M-1)• is a generated submodel of the Kripke model M•.

Proof.The proof is omitted due to space limitations.□

Proposition 6.M,ρ⊨φ if and only if M•,ρ⊩φ.

Proof.It can be proved by induction onφ.We will only consider the case thatφis of the form○ψ.

IfM,ρ⊨○ψ,it follows thatM-1,ρ2⊨ψ.By inductive hypothesis,we get(M-1)•,ρ2⊨ψ.By proposition 5,(M-1)•is generated submodel ofM•.SoM•,ρ2⊩ψ(cf.[1]).Due toρR•ρ2inM•,thus we can getM•,ρ⊩○ψ.

IfM•,ρ⊩○ψ,it follows that there existsρ′such thatρR•ρ′andM•,ρ′⊩ψ.By the definition ofR•,we know thatρ′=ρ[2].Thus,M•,ρ[2]⊩ψ.What is more,by the definition ofS•,we know that eitherρ ∈Ω orρis a suffix of someσ ∈Ω.Either way,we have thatρ[2]is an element of the domain of(M-1)•.Since(M-1)•is a generated submodel of(M•),we then have that(M-1)•,ρ[2]⊩ψ.By inductive hypothesis,we then have thatM-1,ρ[2]⊨ψ.It follows thatM,ρ⊨○ψ.□

The following lemma states that the logical consequence of DML is equivalent to that of standard modal logic on deterministic modal class.

Lemma 1.For each φ ∈LDML,we have thatΓ ⊨φ if and only ifΓ ⊩φ.

Proof.Suppose Γ ⊨φ,but Γφ.This follows that there is a pointed Kripke modelK,ssuch thatK,s⊩Γ butK,sφ.By proposition 4,we can get a DML-model〈S,R,V〉,ρsuch that〈S,R,V〉,ρ⊨Γ and〈S,R,V〉,ρφ,which is contradictory with the premise that Γ ⊨φ.Thus,we have shown that if Γ ⊨φthen Γ ⊩φ.

Suppose Γ ⊩φ,but Γφ.This follows that there is a pointed DML-model〈S,R,V〉,ρsuch that 〈S,R,V〉 ⊨Γ but 〈S,R,V〉φ.We then can construct a Kripke modelM•by definition 8.It follows from Proposition 6 thatM•⊩Γ andM•φ,which contradicts the premise that Γ ⊩φ.Thus,we have shown that if Γ ⊩φthen Γ ⊨φ.□

Definition 9(Deductive system of DML).The deductive system DML is presented in Table 1.

Table 1: The system DML

It can be seen that DML is an extension of the K system of normal modal logic with the axiom Det which characterizes the class of deterministic Kripke models.

Theorem 7.The systemDMLis sound and strongly complete with respect to the semantics ofDML.

Proof.Since the system DML is sound and strongly complete with respect to the class of deterministic Kripke models(see[1]),by Lemma 1,it follows that DML is sound and strongly complete with respect to the semantics of DML.□

4 A Prbabilistic Logic Based on DML

In this section,we construct a probability logic based on the logic DML and give a deductive system of this probability logic.

Definition 10(Language of PLDML).The language of PLDML,denoted asLPLDML,is defined as follows(whereψ1,··· ,ψn ∈LDMLanda1,··· ,an,a ∈Q)

Formulas of the formsa1Pψ1+···+anPψn ▷◁awhere▷◁∈{>,<,≤,=}can be defined inLPLDML(see[3]).

Definition 11(Probability distribution).Let Ω be a finite set.A functionµ: Ω[0,1]is called aprobability distributionover Ω if and only if

Definition 12(Model of PLDML).A PLDML-model is a pair(M,µ)where

·M=〈S,Ω,V〉is a DML-model where Ω is finite;

·µis a probability distribution over Ω.

Definition 13(Semantics of PLDML).The satisfaction relation between a PLDMLmodel(M,µ)and a formulaφ ∈LPLDML,denoted as ⊨,is defined as follows:

Example 2.Imagine drawing a ball from the box in Example 1,but this time without replacement.Assume that these balls are exactly the same except for the color.So for your first draw,the probability of getting red is 0.8(pR),and 0.2 for black(pB).For your second draw,the case will be: if you get a red ball on your first draw,the probability of getting a black ball increases to 0.75,since there are 3 red balls and 1 black ball left.If you get a black ball on your first draw,you will certainly draw a red ball in your next turn,because there is no black ball anymore.This sampling can be depicted by Figure 2.

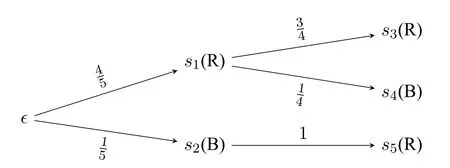
Figure 2: Sampling without replacement

Let the DML-modelM=〈S,Ω,V〉be defined as follows:

·S={s1,s2,s3,s4,s5},

· Ω={s1s3,s1s4,s2s5},

·V(pR)={s1,s3,s5}andV(pB)={s2,s4}.

The probability distributionµon Ω is defined as follows:

We then have the following:

·M,µ⊨PpR=,because ofµ(〚pR〛)=µ({[s1]})=.This means that the probability of the event that you draw a red ball at the first time is.

·M,µ⊨P○pR=,because ofµ(〚○pR〛)=µ({s1s3,s2s5})=.This means that the probability of the event that you draw a red ball at the second time is.

·M,µ⊨P(pR;pB)=,because ofµ(〚pR;pB〛)=µ({s1s4})=.This means that the probability of the successive events that you firstly draw a red ball and secondly draw a black ball is.

Definition 14(Deductive system PLDML).The deductive system PLDMLis presented in Table 2.

Table 2: The system PLDML

The deductive system DML is similar to the deductive system proposed in[3]except for the rule Dst.The premise of the rule Dst in this paper is a formula provable in the system DML.

Proposition 8.If φ1∈LDMLand φ2∈LDMLareDML-inconsistent,we then havethat

Theorem 9(Soundness).The systemPLDMLis sound.

Proof.The key is to show that each axiom is valid and that each rule preserves validity.

Firstly,we will show that each axiom is valid.We will only focus on the axioms of probabilities.

· The axiom NonNeg is valid,i.e.⊨Pψ ≥0.LetM= 〈S,Ω,V〉 be an arbitrary model andµbe an arbitrary probability distribution over Ω.Since〚ψ〛Mis a subset of Ω,it follows by Definition 11 thatµ(〚ψ〛M)≥0.Thus,we have thatM,µ⊨Pψ ≥0.

· The axiom Cert is valid,i.e.⊨P⊤=1.Due to〚⊤〛M=Ω,it follows by Definition 11 thatµ(〚⊤〛M)=1.Thus,we have thatM,µ⊨P⊤=1.

· The axiom Add is valid,i.e.⊨P(ψ1∧ψ2)+P(ψ1∧¬ψ2)=Pψ1.Please note that〚φ1∧φ2〛M=〚φ1〛M∩〚φ2〛M,and〚φ1∧¬φ2〛M=〚φ1〛M∩〚¬φ2〛M=〚φ1〛M ∩(Ω〚φ2〛M)=〚φ1〛M (〚φ1〛M ∩〚φ2〛M).This follows that〚φ1∧φ2〛and〚φ1∧¬φ2〛are disjoint.By Definition 11,we have thatµ(〚φ1∧φ2〛M∪〚φ1∧¬φ2〛M)=µ(〚φ1∧φ2〛M)+µ(〚φ1∧¬φ2〛M).What is more,due to〚φ1∧φ2〛M∪〚φ1∧¬φ2〛M=〚φ1〛M,it follows thatµ(〚φ1〛M)=µ(〚φ1∧φ2〛M)+µ(〚φ1∧¬φ2〛M).Thus,we have thatM,µ⊨P(φ1∧φ2)+P(φ1∧¬φ2)=P(φ1).

Next,we need to show each rule preserves validity.We will only focus on the rule Dst.

Suppose that⊢DMLψ1↔ψ2,by Theorem 7,it follows that the formulaφ1↔φ2∈LPLDMLis valid.We then have that〚ψ1〛M=〚ψ2〛Mfor each DML-modelM.Thus,we have thatµ(〚φ1〛M)=µ(〚φ2〛M).It follows thatM,µ⊨P(φ1)=P(φ2).□

5 Completeness of PLDML

Given a formula set Γ,we useSub(Γ)to denote the minimal extension of Γ such thatSub(Γ)is subformula closed,and useSub+(φ)to denote the minimal extension ofSub(φ) such that ifψ ∈Sub(φ) andψis not a negation formula then¬ψ ∈Sub+(φ).

If Γ is finite,bothSub(Γ)andSub+(Γ)are finite.

Definition 15(DML/PLDML-Atom).Let Γ be a set ofLDML-formulas(LPLDMLformulas).A subsetsofSub+(Γ)is called a DML-atom(PLDML-atom)ofSub+(Γ)if and only ifsis a maximal DML-consistent(PLDML-consistent)subset ofSub+(Γ).

We useAtDML(Γ) to denote the set of all DML-atoms ofSub+(Γ),and we useAtPLDML(Γ) to denote the set of all PLDML-atoms.We useφΘto denote the conjunction of all formulas in Θ if Θ is finite.

Next,we will show that each PLDML-atom is satisfiable.Before that,we need the following two auxiliary propositions.Due to space limitations,the proofs are omitted.

Proposition 10.LetΓbe a finite set of LDML-formulas.We have that the disjunction of all atoms is provable inDML,namely

Proposition 11.LetΓbe a finite set of LDML-formulas and ψ be a formula in Sub+(Γ).We have that

Lemma 2.Given a finitePLDML-atomΘ,there is aPLDML-model(M,µ)such that M,µ⊨ψ for each ψ ∈Θ.

Proof.Let Γ be the set ofLDML-formulas that occurs in Θ.It is obvious that Γ is finite.So,Sub+(Γ) is finite as well.Therefore,there are finite many DMLatoms ofSub+(Γ).Let the set of all the DML-atoms ofSub+(Γ)beAtDML(Γ)={Δ1,··· ,Δn}.

For each 1≤i ≤n,since Δiis DML-consistent,it follows by Theorem 7 that Δiis satisfiable.Let(Mi,ρ)be a pointed model such thatMi,ρ⊨Δi.To indicate this fact,we will write the sequenceρasρΔi

Firstly,we generate the submodelofMifor each 1≤i ≤n.By Proposition 2,it follows that,ρΔi⊨Δifor each 1≤i ≤n.

Secondly,we do the disjoint union ofWe useM= 〈S,Ω,V〉 to denote the disjoint union model.By the definition of disjoint union,it follows that Ω={ρΔ1,··· ,ρΔn}.By Proposition 3,it follows thatM,ρΔi⊨Δifor each 1≤i ≤n.Moreover,since each Δiis a maximal DML-consistent subset ofSub+(Γ),it follows that any two atoms Δiand Δjwhere 1≤i,j ≤nare DML-inconsistent.Therefore,any two atoms are not satisfiable.Thus,each Δiis only satisfied byM,ρΔi.So,we have that〚Δi〛M={ρΔi}.

Next,we need to show that there is a probability distributionµover Ω such thatM,µ⊨Θ.

By a similar process presented in [3],it can be proved that there indeed is a probability distributionµover Ω such that

· If(a1Pψ1+···+ajPψj ≥a)∈Θ,thenM,µ⊨a1Pψ1+···+ajPψj ≥a.

· If(a1Pψ1+···+ajPψj ≥a)Θ,thenM,µa1Pψ1+···+ajPψj ≥a.

Due to space limitations,the proof details of this result are omitted.With this result,it can be shown by induction onφthat for eachψ ∈Sub+(Θ),

It follows thatM,µ⊨ψfor allψ ∈Θ.□

Theorem 12(Weak completeness).The systemPLDMLis weak complete,that is,if a formula φ ∈LPLDMLisPLDML-consistent then it is satisfiable.

Proof.Sinceφis PLDML-consistent,it follows by Lindenbaum’s lemma that there is a PLDML-atom Θ ofSub+(φ)such thatφ ∈Θ.By Lemma 2,we then have that there is a PLDML-modelM,µsuch thatM,µ⊨ψfor allψ ∈Θ.Thus,φis satisfied byM,µ,then it is satisfiable.□

6 Conclusion

In this paper,we propose semantics for a modal language to capture the reasoning about successive events in probability theory.We prove that this logic(called DML)is equivalent to the normal modal logic on deterministic Kripke models.We then construct a probability logic on DML and show the completeness of its deductive system PLDML.

There is no nesting of probabilistic operators and modal operators in the probability logic PLDML.Hence,one of the natural future directions is to extend PLDMLto allow nesting probabilistic operators and modal operators.This will allow us to express formulas like ”φ;(Pψ=a)”,which could help us to reconsider the notion of independence in probability theory.Traditionally,the independence of two eventsAandBis defined asµ(AB)=µ(A) ×µ(B).This definition is challenged in various aspects(see[8]).We suggest that independence might be defined asφ;Pψ=a ↔P((φ∨¬ψ);ψ)=a,which means that the occurrence ofφhas no effect on the probability ofψ(see[8]).We will investigate this definition of independence in future work.