具有非线性耦合的分数阶神经网络的聚类同步
王 雪,丁小帅,李 剑
(陕西科技大学 数学与数据科学学院,陕西 西安 710021)
分数阶微积分[1-2]是指阶次为分数且与Γ 函数[3]密切相关的基本运算,因其以加权形式积累了函数的全局信息,被广泛用于描述实际中具有记忆特性或历史依赖性的现象和过程,构建更加精确的数学模型。目前,分数阶微分系统被广泛应用于图像处理[4]、量子演化[5]、反常扩散[6]、黏弹性材料[7]等领域。
神经网络是基于网络拓扑理论来模拟人脑神经突触对复杂信息进行处理的模型,其具有大规模并行处理、分布式存储和非线性运算等特点,因此具有较强的运算能力、容错能力和自组织能力。近年来,分数阶微积分被引进神经网络的建模中[8-10],使得模型的设计、表达和控制能力得到进一步的提高。
同步是非线性动态网络中的一种合作行为,指的是多个系统通过信息交互彼此影响,最终实现相同状态的过程。根据不同的表现特征,同步又可分为多种形式,如投影同步[9]、完全同步[10]、聚类同步[11]等。其中,聚类同步指的是将一个网络系统分为不同的簇,同簇内的节点互相实现同步,而不同簇的节点最终具有不同状态的过程。现实中,许多网络由于特定的目标需要按照功能被划分为不同的类别,因此,神经网络的聚类同步得到了广泛关注。
另外,为了实现同步目标,需要选择适当的控制策略,常见的同步方法有脉冲控制[12]、采样控制[13]、牵引控制[14]、自适应控制[15]、事件触发控制[16]、反馈控制[17]等。值得一提的是,牵引控制只需对一部分节点设计控制器就可以实现整个网络的同步目标,具有较小的控制成本。而脉冲控制是一种不连续控制方法,具有安装方便、可靠性强和维护成本低等优点。基于此,很多学者结合二者优势,研究了系统的牵引脉冲控制。文献[18]和文献[19]分别研究了基于牵引脉冲控制的复值神经网络的同步问题和随机神经网络的聚类同步问题;文献[20]采用牵引脉冲控制研究了分数阶复杂动力网络的指数同步问题;文献[21]通过牵引脉冲控制实现了分数阶切换神经网络的聚类同步。但是,借助牵引脉冲控制策略,研究带非线性耦合项的分数阶神经网络的聚类同步控制问题的文献并不多见。
本文针对具有不确定参数的非线性耦合分数阶神经网络,研究其在牵引脉冲控制作用下与驱动节点实现聚类同步的问题。选择基于平均脉冲区间的牵引脉冲控制策略,给出分数阶神经网络实现聚类同步的充分条件。
1 预备知识
1.1 符号说明
C、R、Z+和R+表示复数集、实数集、正整数集和正实数集;Rn表示n 维实数列向量,Rn×m表示n × m维实数矩阵;In表示n 维单位矩阵;‖·‖表示矩阵或向量的2-范数;对于矩阵K,KT表示其转置矩阵,λmax(K)表示其最大特征值,K >0 或K <0 表示K为正定矩阵或负定矩阵,KS=(K+KT)/2;定义A=(N,E,R)表示图论,其中N={1,…,N}表示节点集,E ⊆N × N 表示边缘集,R∈RN×N表示耦合矩阵;A 被分为m 个聚类,标记为C1={1,…,v1},C2={v1+1,…,v2},…,Cm={vm-1+1,…,vm},其中vm=N。
1.2 分数阶微积分概述
定义1[22]连续可微函数f(·)的α 阶Caputo 分数阶微分定义为
其中t≥t0,0 <α <1,Γ(·)为Γ 函数。
定义2[23]对任意σ∈C,具有双参数α,β∈R+的Mittag-Leffler 函数定义为
当β=1 时成为单参数的Mittag-Leffler 函数,其定义为
特别地,当α=β=1 时,其定义为
引理1[24]假设x(t)∈Rn是可微的函数向量。若V(t)为区间[t0,+∞]上的连续函数,并且满足≤φV(t,x(t)),则
成立,其中,0 <α <1,φ <0。
1.3 神经网络模型描述
本文考虑一类具有非线性耦合的分数阶延迟神经网络模型
其中:0 <α <1;t≥t0;i∈Cp;p=1,2,…,m;xi(t)∈Rn表示第i 个节点的状态向量;f(xi(t))=(f(xi1(t)),…,f(xin(t)))T∈Rn表示激活函数;Φ(xj(t))=(Φ(xj1(t)),…,Φ(xjn(t)))T∈Rn表示非线性耦合函数;Ap=diag{ap1,…,apn} >0 表示第p 聚类的自反馈矩阵;Bp∈Rn×n表示第p 聚类的连接矩阵;ΔAp∈Rn×n和ΔBp∈Rn×n表示不确定系 数;d表示耦合强度;H=diag{h1,…,hn} >0 表示内部耦合矩阵;ΔH∈Rn×n表示不确定内部耦合矩阵;R=(rij)∈RN×N表示外部耦合矩阵,其满足Ip(t)∈Rn表示第p 聚类的外部输入向量;ui(t)∈Rn表示控制输入向量。
假设1对任意的x,y∈R,存在常数k≥0使得
假设2对任意的x,y∈R,存在常数β >0,∊k>0,函数ak(x),bk(x)使得
其中k=1,…,n。
注1非线性耦合问题广泛存在于实际的分数阶复杂动态网络中。利用适当的投影策略,可以将非线性耦合函数分解为振荡部分和线性部分βx。
假设3考虑到参数的不确定性会对分数阶神经网络的聚类同步产生影响,假设不确定参数矩阵ΔAp,ΔBp满足
其中k1>0,k2>0。
注2在实际应用中,由于系统建模误差、外界干扰和参数波动等因素的影响,神经网络的参数可能存在偏差,从而导致参数的不确定性。
假设4耦合矩阵R 可写成分块形式
本文所考虑的误差系统可描述为
其中i∈Cp,p=1,…,m。定义映射ψ:{1,2,…,N}→{1,2,…,m},则式(7)还可表示为ei(t)=xi(t)-SCφ(i)(t),其中,ψ(i)=p,p=1,…,m,i=1,…,N。
定义3[25]如果存在p,q=1,…,m,满足
其中i∈Cp,p≠q,则称分数阶神经网络(5)与(6)是聚类同步的。特别地,当p=1 时,v1=N,聚类同步退化为完全同步。
对于未添加控制的神经网络(5),同一聚类中节点的轨迹往往不同,这意味着聚类所含节点轨迹与目标轨迹(6)存在偏差,因此,需要对原网络设计适当的控制器,以实现同步目标。我们选择牵引脉冲控制策略,在同一聚类的部分节点上添加脉冲控制。
设计一个统一的脉冲控制器
引入脉冲控制器(10),则系统(5)与系统(6)的误差系统描述为
引理2[21]对于任意μ >0,X,Y∈Rn,P∈Rn×n使得
2 主要结论
在本节中讨论一类具有非线性耦合的分数阶神经网络在牵引脉冲控制下实现系统(5)和系统(6)的聚类同步。
其中:Θ=diag(θ1,θ2,…,θn);
(5)在牵引脉冲控制下与系统(6)是聚类同步的。
证明:构造Lyapunov 函数
当t∈[tn,tn+1]时,对式(14)两边求α 阶分数阶导数可得
根据假设1、假设3 和引理2 有
由式(18)—(21)得
下面讨论耦合节点情况,根据假设2、假设3、引理2、引理3 和引理4 有
其中,
由式(23)和(24)得
根据式(22)和(25)有
根据式(13)可推得
由引理1 可得
根据式(28)和(29)可知,当t∈[t0,t1)时,有
当t∈[t1,t2)时,有
当t∈[tn,tn+1)时,有
由上述分析可知,当t≥t0时,
式(30)可进一步表示为
特别地,当α=1 时,系统(5)变为整数阶神经网络,即
其中:t≥0;i∈Cp;p=1,…,m。
假设SCp(t)∈Rn表示第p 聚类中孤立节点的状态,其满足方程
将系统(33)作为响应系统,系统(34)作为驱动系统,在脉冲控制器(10)的作用下,系统(33)和系统(34)可得到下面的同步性结论。
推论1在假设1、假设2 和假设3 成立的前提下,给定常数μ1>0,μ2>0,β>0,矩阵Θ>0,Υ>0,存在矩阵K >0,G >0,使得式(13)成立,则系统(33)在牵引脉冲控制下与系统(34)是聚类同步的。
当t≥t0时,有
当t→∞时,有V(t)→0。因此,在脉冲控制器(10)的作用下,系统(33)和系统(34)是聚类同步的。
证毕。
当p=1 时,v1=N,则系统(5)变为
假设S(t)∈Rn表示孤立节点的状态,其满足方程
将系统(35)作为响应系统,系统(36)作为驱动系统,在脉冲控制器(10)的作用下,系统(35)和系统(36)可得到下面的同步性结论。
推论2在假设1、假设2 和假设3 成立的前提下,给定常数μ1>0,μ2>0,0 <α <1,β >0,矩阵Θ >0,Υ >0,存在矩阵K >0,G >0 使得式(13)成立,则系统(35)在牵引脉冲控制下与系统(36)是同步的。
证明:类似于定理1 的证明,故略去。
3 数值仿真
考虑具有非线性耦合的分数阶神经网络为
假设系统(37)中各簇的孤立节点状态为
则由定理1 可知,系统(37)和系统(38)在脉冲控制器(10)下是聚类同步的。
给定初值φ=(1.5,-6,6,-3,1.5,-5,-6.5,-2.3,6,2,-5.3,6.5,-2.4,1,-5.3,-5.8,-3,6.5,2.5,-6.5,5.8,-3.4,0.7,-4.6,-6.8,-2.7,5.8)T。在脉冲控制器(10)的作用下,系统(37)的状态轨迹如图1 所示,系统(37)和系统(38)的误差范数‖e(t)‖的演化如图2 所示,由此易得系统(37)和系统(38)是聚类同步的。

图1 在控制器(10)的作用下系统(37)的状态轨迹(i=1,2,…,9)Fig.1 State trajectories of system(37)under controller(10)(i=1,2,…,9)
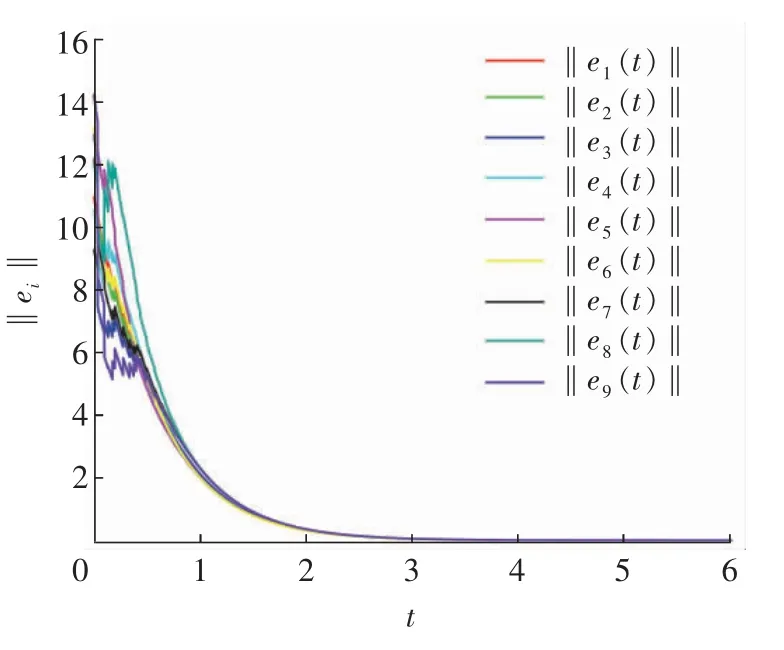
图2 系统(37)和系统(38)的误差范数‖e(t)‖的演化Fig.2 Evolution of error norm ‖e(t)‖ of system(37)and system(38)
当α=1 时,系统(37)退化为系统(33),定理1中的条件(13)仍适用于系统(33)。在脉冲控制器(10)下,系统(33)的状态轨迹如图3 所示,系统(33)和系统(34)的误差范数‖e(t)‖的演化如图4所示,由此易得系统(33)和系统(34)是聚类同步的。

图3 在控制器(10)的作用下系统(33)的状态轨迹(i=1,2,…,9)Fig.3 State trajectories of system(33)under controller(10)(i=1,2,…,9)

图4 系统(33)和系统(34)的误差范数‖e(t)‖的演化Fig.4 Evolution of error norm ‖e(t)‖ of system(33)and system(34)
4 结束语
本文针对具有不确定参数的非线性耦合分数阶神经网络,设计了基于平均脉冲区间的牵引脉冲控制器对部分节点进行控制,实现了网络的聚类同步。此外,构造合适的Lyapunov 函数,并利用不等式放缩技巧,建立了保守性较小的聚类同步准则。仿真实验表明了脉冲控制器的有效性,同时也验证了理论结果的正确性。

