Mlinex损失函数下反向帕累托分布形状参数的Bayes估计
何贵阳,周菊玲
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
帕累托分布是一类经典的,能充分反映幂律特征的分布函数,因此一直备受关注。其名称是由意大利经济学家维弗雷多·帕累托(1848—1923)定义的,这一分布在经济学以外领域被称为“布拉德福分布”。因帕累托分布中变量的独特取值要求,即定义变量取值在特定数值之上,使得帕累托分布在应用上受限。如黄娟等人讨论了Pareto 分布参数的经验Bayes(EB)单边检验问题,构造了参数的经验Bayes 检验函数,证明了其具有渐近最优性,并且获得了收敛速度[1]。李超建等人介绍了基于帕累托分布的禽畜种苗交易系统入侵容忍模型,每台服务器的结构不同,但禽畜种苗交易网站服务内容相同,具有响应结果一致性[2]。温利民等人建立贝叶斯模型,讨论帕累托索赔额分布中参数的估计问题,得到了风险参数的极大似然估计、贝叶斯估计和信度估计,并证明了这些估计的强相合性[3]。钱小仕等人提到地震震级超过某一阈值的超出量分布可以近似为广义帕累托分布,并介绍了基于广义帕累托分布给出的若干地震活动性参数的估计公式[4]。张悦基于多种复杂删失数据研究帕累托分布的统计特性,构建了逐步II 型删失下的拟合优度检验,推导了广义逐步II型删失下帕累托分布的寿命绩效指数的统计推断,讨论了适应性逐步II型删失模式下帕累托分布的竞争风险模型分析,并将结论推广到更复杂的广义指数分布[5]。通过查阅近些年关于帕累托分布的相关研究文献,可以确定帕累托分布只局限于刻画幂律特征的分布函数中的上尾部分[1-7]。从此特性出发,考虑变量的取值,如果将帕累托分布变量的定义域取相反数,则可以求解其受限外的区域,即刻画幂律特征的分布函数中的下尾部分。王超探讨了反向帕累托分布的统计推断问题,通过研究2010年我国655个城市人口规模,证明了中小型城市人口规模可以使用反向帕累托分布进行拟合[8]。简单的取值变化弥补了帕累托分布刻画区域的不足,同时也完善了对满足幂律特征区域的一种刻画问题。针对帕累托分布变量取相反数的特点,结合帕累托分布特点,提出反向帕累托分布。反向帕累托分布的密度函数和分布函数分别为
其中,a和λ分别为位置参数和形状参数,且a>0,λ>0,符号表示为RP(a,λ).
在处理参数估计问题上,常见方法有极大似然估计、矩估计、熵估计、Bayes估计等。根本上是频率学派与贝叶斯学派就估计方法进行激烈讨论,其中频率学派的极大似然估计与贝叶斯学派的最大后验估计最具代表性。但无论是哪一学派的哪一种估计方法,都离不开样本信息与损失函数的选取,其中常用的损失函数有熵损失函数、平方损失函数、加权平方损失函数、Linex 损失函数、复合Linex 损失函数、Mlinex 损失函数等。值得一提的是Mlinex 损失函数,Mlinex 损失函数是一类非对称损失函数,是由Podder 在2004 年提出的一种修正的线性指数损失函数,其具体表达式为
其中,θ是未知参数λ判别空间的一个估计。Mlinex 损失函数虽是对原有损失函数的一种修正,但一直未停止对其进行研究。例如王琳等人基于逐步增加Ⅱ型截尾样本,研究了Mlinex 损失下BurrⅫ部件可靠性指标的经验Bayes 估计[9]。丁新月等人在Mlinex 损失函数下,讨论了逆伽马分布尺度参数的Bayes 估计及其可容许性[10]。李新鹏等人利用信度理论的方法得到了Mlinex 损失函数下Bühlmann-Straub 模型具有特殊相依效应的信度保费,进而推导出Mlinex损失函数下Bühlmann模型具有此种相依效应的信度保费[11]。
事先说明Mlinex 损失函数中常数c的取值问题。文章只研究c>0 的情况,c<0 的情形类似,不做充分讨论。文章第一节为预备知识;第二节对频率学派极大似然估计与贝叶斯学派最大后验估计进行讨论,并推导反向帕累托分布形状参数在最大后验估计方法下的具体表达式;第三节介绍了在Mlinex 损失函数下反向帕累托分布形状参数的经典Bayes 估计,并推导出具体表达式;第四节在Mlinex 损失函数下,讨论反向帕累托分布形状参数的多层Bayes估计与E-Bayes估计;第五节通过数值模拟,验证所列举估计方法的准确性、稳健性、可靠性;第六节在参数最优环境下,利用最优估计方法,进行数据拟合,确定新疆县市级城市的人均城市道路面积可以利用反向帕累托分布近似拟合,并结合最终数据给出相应的数据分析。
1 预备知识
在处理待估参数是客观存在但未知的一类估计问题时,常用的估计方法是经典频率学派观点下的极大似然估计(MLE)。
引理1[9]若X1,X2,…,Xn是来自RP(a,λ)分布的简单随机样本,其中a与λ分别为位置参数与形状参数。令X=(X1,X2,…,Xn),并且x1,x2,…,xn是其相应随机样本下的观察值,则RP(a,λ)中位置参数a与形状参数λ的极大似然估计分别为
在实际应用时,发现个别待估参数与样本有关,针对这类情况,贝叶斯学派提出了最大后验估计(MAP)方法。其估计原理是考虑待估参数的先验信息与样本信息有关,需选择合适的估计量使得后验分布密度达到最大值[12],同时最大后验估计作为Bayes估计的一种近似解,也有一定的研究价值。
2 形状参数λ的最大后验估计
由于参数λ的最大后验估计应使后验分布达到最大[12]。即选定合适的估计量使p(X|λ)π(λ)达到最大,其中π(λ)是参数λ的先验分布密度,p(X|λ)是样本X1,X2,…,Xn对参数λ的条件密度。从处理参数估计问题的原理上可以看出,极大似然估计是最大后验估计在π(λ) ∝1的先验分布。接下来利用这一特点结合引理1给出的极大似然估计方法,推导出形状参数λ的最大后验估计方法。
定理1若X1,X2,…,Xn是来自RP(a,λ)分布的简单随机样本,其中a与λ分别为位置参数与形状参数。令X=(X1,X2,…,Xn),并且x1,x2,…,xn是其相应随机样本下的观察值,选取Γ(β,γ作为形状参数λ的先验分布π(λ),则在位置参数a已知的情况下,形状参数λ的最大后验估计为
证明选取形状参数λ的先验分布为其中参数β,γ为超参数,且β>0,γ>0,同时令p(X|λ)是样本X1,X2,…,Xn对参数λ的条件密度,则有
考虑到形状参数λ的最大后验估计是寻找λ的估计量,使形状参数λ的后验密度函数达到最大值的情况,即找到使p(X|λ)π(λ)达到最大值。
令g(λ)=λn+β-1e-(γ-t)λ,由最大后验估计方法的原理可知,要对p(X|λ)π(λ)关于λ求解最大值,就是要对g(λ)关于λ求解最大值。但关于g(λ)直接求解最值问题处理较为复杂,考虑变式,因g(λ)=exp{ln(g(λ))}=exp{ln(λn+β-1e-(γ-t)λ)},则对g(λ)求解最值问题可转化对ln[g(λ)]求解最值问题。
对ln[g(λ)]关于形状参数λ取一阶微分,同时令微商为0,即
3 形状参数λ的Bayes估计
上文介绍了反向帕累托形状参数λ的最大后验估计。由于最大后验估计是Bayes 估计解的近似值,其估计结果相比于利用Bayes 理论下的经典估计方法得到的结果,还存在一定偏差。具体体现在损失函数的影响,所以下面将继续讨论在考虑损失函数情况下,反向帕累托形状参数λ在Bayes 理论下的经典估计方法并确定估计结果的具体表达式。
考虑位置参数a已知的情况下,形状参数λ在Mlinex损失函数下的经典Bayes估计问题。
定理2设X1,X2,…,Xn是来自RP(a,λ)分布的简单随机样本,其中a与λ分别为位置参数与形状参数。令X=(X1,X2,…,Xn),并且x1,x2,…,xn是相应随机样本下的观察值,在Mlinex 损失函数(1)下,对于任意的先验分布π(λ),在位置参数已知的情况下,形状参数λ的唯一Bayes估计为
其中,p(X|λ)π(λ)表示参数λ与样本X=(X1,X2,…,Xn)的联合密度函数。
由损失函数定义可知,在对特定分布的参数进行估计时,考虑到给定相应损失函数后,需要使风险函数尽可能的小,以保证参数估计时的准确性。为此需使风险函数中的极小化即可。
因为
将f((X))关于(X)求一阶微分并令其等于零,便可解得形状参数λ的Bayes估计为
由于f((X))是凸函数,所以(X)是f((X))的唯一最小值。同时若存在λ'使得R(X)(λ) <∞,对于参数λ的Bayes估计(X)是唯一存在的且是可容许的,所以可以确定形状参数λ的唯一Bayes估计一般形式为
推论1同定理2条件。选取作为RP(a,λ)分布中形状参数λ的先验分布π(λ),其中参数β,γ为超参数,且β>0,γ>0,在Mlinex 损失函数(1)下,且位置参数a已知的情况下,形状参数λ的Bayes 估计的精确表达式为
证明因为选取作为形状参数λ的先验分布π(λ),则由式(2)可得
又因为RP(a,λ)分布的密度函数是f(x;a,λ)=λa-λxλ-1;0 <x≤a,λ>0,所以样本的似然函数由式(3)确定为
由式(5)可以看出,形状参数λ的后验分布服从伽马分布Γ(n+β,γ-t).
于是有
因此,由定理2可知,Mlinex损失函数下形状参数λ的Bayes估计的精确表达式为
4 形状参数λ的E-Bayes估计(EB)与多层Bayes估计(HB)
在Bayes 理论不断进步的同时,对特定分布参数的估计方法也一直不断地发展与完善。这一系列的发展也使得参数估计不断逼近于真值,使其误差不断地缩小,这样的结果正是对特定分布参数进行估计的最终理想。所以接下来文章进一步研究形状参数λ在Mlinex 损失函数下,先验分布选定为Γ(β,γ) 的E-Bayes估计与多层Bayes 估计。根据相应文献,为了使估计的效果较好,Γ(β,γ) 中参数β和γ的取值应使先验分布密度函数为形状参数λ的减函数[13]。再考虑估计的稳健性,最终确定0 <β<γ<m,其中m为常数[14]。
4.1 E-Bayes估计(EB)
定义1对于(a,b)∈D,若B(a,b)是连续的,则称是参数λ的E-Bayes 估计,其中∬DB(a,b)f(a,b)dadb是存在的,D是超参数a和b的取值集合,f(a,b)是a和b在集合D上的密度函数,B(a,b)为λ的Bayes估计。
从定义可以看出,参数λ的E-Bayes估计
是参数λ的Bayes估计B(a,b) 对超参数a和b的数学期望,即λ的E-Bayes估计是λ的Bayes估计对超参数的数学期望。
定理3设X1,X2,…,Xn是来自RP(a,λ)分布的简单随机样本,其中a与λ分别为位置参数与形状参数。选取Γ(β,γ) 作为形状参数λ的先验分布π(λ),其中参数β,γ为超参数,且β>0,γ>0.令X=(X1,X2,…,Xn),并且x1,x2,…,xn是相应随机样本下的观察值,在位置参数已知时,RP(a,λ)分布中的形状参数λ,在Mlinex损失函数下的E-Bayes估计的精确表达式为
证明首先由推论1 可知,RP(a,λ)分布的形状参数λ,在Mlinex 损失函数下的Bayes 估计的精确表达式为
最后由定义1,RP(a,λ)分布的形状参数λ,在Mlinex损失函数下的E-Bayes估计的精确表达式为
4.2 多层Bayes估计(HB)
定义2若λ的先验分布为Γ(β,γ)分布,其密度函数其中参数β,γ为超参数,且β>0,γ>0.假设β,γ独立,则有β和γ的先验分布分别为上的均匀分布,所以得到先验分布密度函数f(β,γ)=,同时在β和γ独立时,则λ的多层先验密度函数为
定理4同定理3条件。在位置参数a已知时,若形状参数λ的多层先验密度函数π*(λ) 由定义2给出,则在位置参数已知时,在Mlinex下形状参数λ的多层Bayes估计为
证明设X1,X2,…,Xn为来自RP(a,λ)分布的简单随机样本,在位置参数a已知时,样本的似然函数由式(3)给定
若形状参数λ的多层先验密度函数由定义2给出,根据Bayes定理,形状参数λ的多层后验分布密度为
5 数值模拟
文章研究了形状参数λ的五种估计方法并给出了相应的具体表达式。为确保估计所得结果的准确性、稳健性,接下来利用R 软件对给出的估计方法进行MC 数值模拟,并在模拟中运用控制变量的原理,观察对比偏差量Abs 的数值变化,逐步得到最优估计的参数环境。在最优估计参数环境下,通过对均方误差MSE的数值变化进行讨论,最终确定Bayes理论下的最优估计。
在RP(a,λ) 分布中,给定参数真值,即位置参数a=100 和形状参数λ=3 时,对样本取值为n=20、50、100、150,Mlinex 损失函数相应参数ω=1、形状参数λ的先验分布为Γ(2,1) 均给定。采用MC 方法进行数值模拟计算,每种情况均进行2000次模拟计算,其计算结果如表1、表2、表3所示。其中,表1为给定条件下,确定Mlinex损失函数中常数c的最优环境;表2为给定条件下,确定形状参数λ的先验分布下参数的最优环境;表3为在最优环境下形状参数λ的三种估计方法下的均方误差MSE.

表1 确定Mlinex损失函数中常数c的最优环境(给定条件)
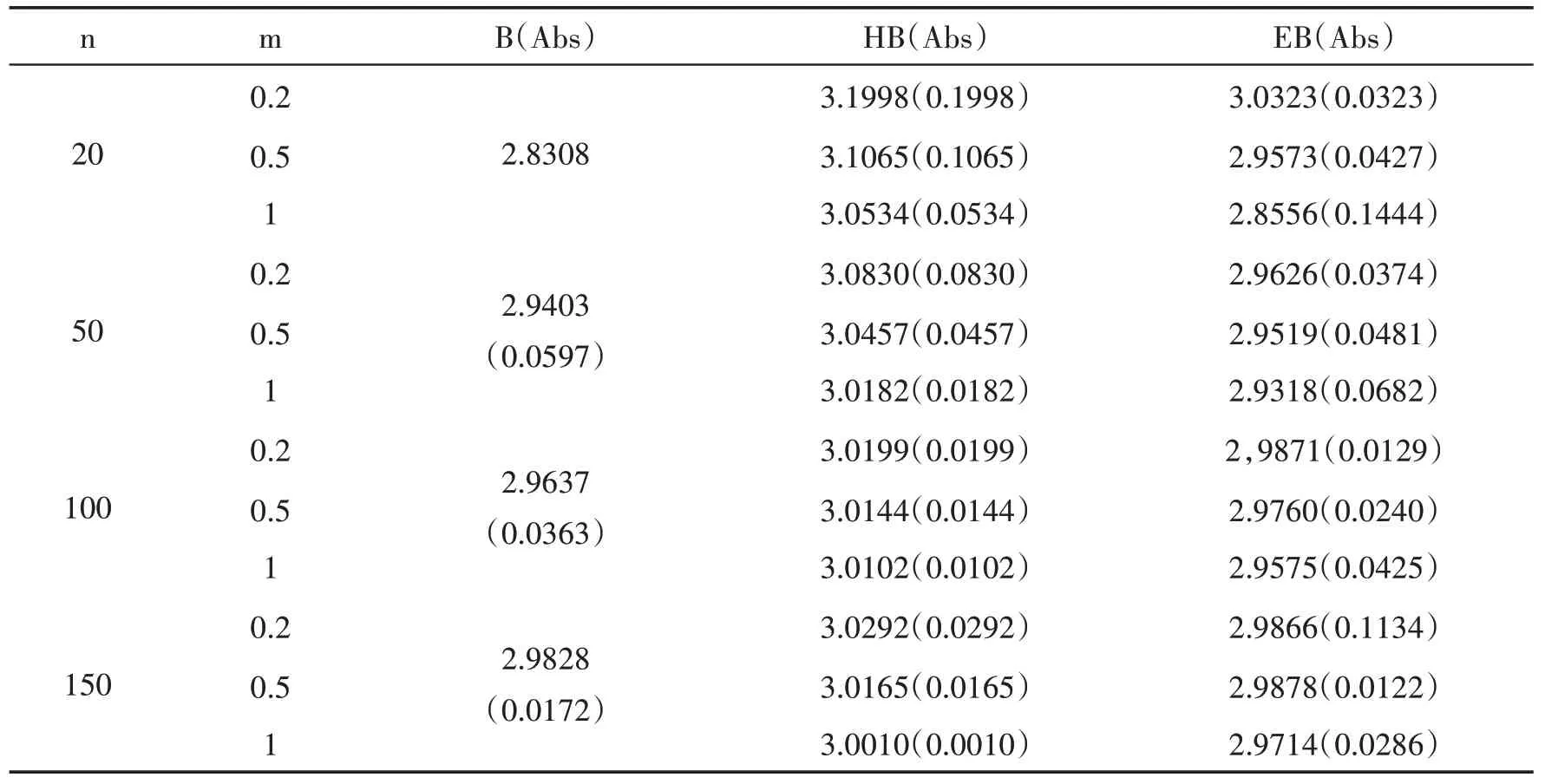
表2 确定形状参数λ的先验分布中参数的最优环境(给定条件)

表3 在最优环境下形状参数λ的三种估计方法下的均方误差MSE

表4 2021年新疆20座县市级城市人均城市道路面积数据
由表1数据可得结论如下:
(1)与近似Bayes估计方法和Bayes估计方法相比,基本估计方法中极大似然估计结果比真值大,即偏差量为正。相比于极大似然估计,最大后验估计结果更接近真值。这是最大后验估计在估计问题上考虑了待估参数先验分布与样本相关的体现。
(2)Mlinex 损失函数中常数c的取值变化对RP(a,λ)分布中形状参数λ的Bayes 估计有一定的影响。可以看出,当Mlinex 损失函数常数c=1 时,其估计结果最接近真值,所以可以判断在已给定条件下,Mlinex 损失函数参数的最优环境为ω=1,c=1.
(3)对比三种估计方法在样本容量逐步增大时,估计结果也逐步趋近真值,即三种估计方法均满足大样本性质。同时对比偏差量可知所列举估计方法得到的结果是准确的,估计结果均满足准确性。
(4)结合数据可以判断出,在无损失函数环境影响下,处理满足反向帕累托分布形状参数的大样本数据的估计问题上,选择最大后验估计是最优的。
由表2数据可得结论如下:
(1)在Bayes 理论下,相比于经典Bayes 估计(B)和E-Bayes 估计(EB),多层Bayes 估计(HB)估计结果的偏差为正偏差量,其他两个为负偏差量。
(2)形状参数λ的先验分布中参数的数值选取对Bayes 估计结果有一定的影响,可以看出当先验分布中参数的数值选取m=1时,其估计结果最接近真值。所以可以判断在已给定条件下,形状参数λ的先验分布中参数的数值选取最优环境是m=1.同时对比m取值量的变化,三种Bayes 估计方法得到结果变化的幅度都较小,即可说明三种Bayes估计方法所得结果均满足稳健性,其中E-Bayes估计稳健性最强。
(3)同表1结论,以上三种Bayes方法也均满足大样本性,估计结果均满足准确性。
(4)结合数据可以判断出:在Mlinex 损失函数环境影响下,如需准确地处理满足反向帕累托分布形状参数的大样本数据估计问题时,选择E-Bayes估计方法是最优的。如需处理满足特定的正偏差逼近问题时,可选择多层Bayes估计方法得到较准确的近似值。
由表3数据可得结论如下:
(1)在参数的最优环境下,Bayes 理论中的三种估计方法所得结果的均方误差MSE 数值变化较稳定,结果能体现三种Bayes 估计方法的合理可靠性。同时随着样本数据的增加,均方误差MSE 均控制在较小的有效值内,即三种Bayes估计方法所得结果是准确有效的。
(2)数据对比可得:三种Bayes 方法的均方误差MSE 偏差量,在大样本数据下均控制在0.001,即三种Bayes 估计方法所得结果较相近。同大样本数据下,E-Bayes 估计方法中均方误差MSE 控制较好,其可靠性较其他两种较强。
6 结论
文章所给出的包括近似Bayes 与Bayes 理论下常用的三种估计方法,通过数值模拟并分析比较,得到以上五种估计方法都满足大样本性质且部分估计结果具有一定的可靠性、准确性、稳健性。结合样本条件与稳健性要求,五种估计方法中E-Bayes估计法,在处理Mlinex损失函数下反向帕累托分布形状参数的估计问题上较为快捷、准确、稳定,即可判断E-Bayes估计是最优估计方法。
7 实例应用
文章1—4 节内容已解决了所提出的估计问题,并最终做出总结,给出了处理相应参数估计问题的最优方法。但理论研究不仅仅是对处理问题的方法进行总结,更是要解决实际问题。在对反向帕累托分布的研究中,鲜有见到相关实际问题的讨论。王超探讨了反向帕累托分布的统计推断问题,通过2010 年我国655个城市人口规模的案例,证明了中小型城市人口规模可以使用反向帕累托分布进行拟合[8]。蓝海等人基于E-Bayes 估计的定义,分别在加权平方损失函数和平方损失函数下讨论了反向帕累托分布在位置参数已知时,形状参数α的E-Bayes估计[15]。徐宝等人使用加权p,q对称损失函数研究了反向帕累托分布的形状参数在刻度参数给定条件下Bayes 估计的形式与性质。得到了形状参数Bayes 估计的一般形式以及在给定共轭先验下的精确形式,证明了所得Bayes 估计具有可容许性以及最小最大性[16]。文章将从文献[16]提出的反向帕累托分布可以拟合中小型城市人口规模的研究出发,对新疆维吾尔自治区二十座县市级城市的人均城市道路面积进行拟合研究。
一座城市的发展,不仅仅依赖于经济水平的提升,经济的发展与城市道路面积的扩建也体现在城市常住人口数的变化,但要考虑到经济发展同时伴随着人口流动。面对近些年不断发展的新疆,常住人口数已不能再作为衡量某座城市的发展标准,所以文章引入人均城市道路面积作为城市发展的判断依据。文章利用反向帕累托分布对新疆维吾尔自治区内二十座县市级城市的人均城市道路面积进行拟合,并利用最优估计方法判断拟合结果是否准确。以下数据来自于新疆维吾尔自治区统计局《2021 年新疆统计年鉴11-2 各城市市区设施水平》。
通过分析,设表中数据为X=(X1,X2,…,X20)的样本,通过计算得到样本均值与样本方差:E(X)=32.50,Var(X)=345.50.观察样本数据分布情况,有较多的小样本数据。同时结合人口分布的特点,数据可视为满足幂律特征的下尾分布,即考虑利用反向帕累托分布拟合。通过反向帕累托分布期望与方差公式
结合样本均值与样本方差信息,求解得到参数真值a≈64.561,λ≈1.014.但由于限定0 <x≤a,所以上述表格中存在异常数据,从而限制了参数a的确定。对比实际人口数据判断阿拉山口市与霍尔果斯市数据存在一定异常,主要体现为流动人口数较多,常住人口数较其他地区偏少,使得在同等城市道路面积下,人均城市道路面积值偏大。
利用Excel 软件,在理想环境下,对已知的20 组数据进行参数的E-Bayes 估计。通过迭代拟合,修正参数a的值并对估计结果与真值进行数值比较,在误差可允许范围内找到最优估计下参数的近似估计值,最后验证拟合的准确性。
由表5拟合结果可以得出:

表5 通过迭代修正参数a的值并对参数λ拟合,得到近似拟合值y(理想环境)
(1)2021 年新疆城市市区设施水平中人均城市道路面积数据可以用反向帕累托分布近似拟合,拟合结果相对准确。
(2)在处理2021年新疆城市市区设施水平中人均城市道路面积数据时,发现在给定数据的情况下,得到的参数a的真值存在误差,在后期数据拟合中,也验证了数据中阿拉山口市与霍尔果斯市数据存在异常。在数据不变的条件下,通过Excel软件的迭代修正参数a数值,并对修正后数据进行估计。对比参数λ真值,可以判断当a=244 时,估计结果与真值相同,数据拟合最完美。同时确定当a∈[136,845]时,数据均方误差MSE ≤0.3640,即在可偏差范围内。
(3)在对参数a进行修正过程中发现,表中给定的数据中存在异常,但异常不是错误。根据对资料的查询与研究,找到阿拉山口市与霍尔果斯市数据异常原因为:该地区人口数据变化幅度较大,即流动人口数较多,常住人口数量较少,人口流动性较强。同时也说明该地区城市公共资源开发力度较强,开发后使用程度较低等问题。
(4)对比全国人居城市道路面积数据可以判断,以上城市中较多数城市数据高于全国标准数据17.36 m2.即说明新疆县市级城市资源利用率较低,固定人口数较少,人口流动性较强。
8 总结
文章对Mlinex 损失函数下反向帕累托分布形状参数估计进行充分讨论,对比了频率学派的极大似然估计与贝叶斯学派的最大后验估计两大经典估计方法,两者的估计结果在数值上较为相似。结合两者在处理问题上的出发点不同,所以应用也各不相同。同时文章也在Bayes 理论下,对相应参数进行了近似Bayes 估计与经典Bayes 估计的对比,给定了形状参数在估计时的参数最优环境,并通过数值模拟得到在Bayes 理论下,处理相应估计问题的最优估计,即E-Bayes估计是最优估计方法。最后利用最优估计方法,对《2021年新疆统计年鉴11-2 各城市市区设施水平》中人均城市道路面积的数据进行参数拟合,确定了新疆县市级城市的人均城市道路面积可以利用反向帕累托分布拟合,并结合最终数据给出了相应的数据分析。

