时空团状系数回归模型及其在海洋时空断面数据中的应用*

付昊天, 李芙蓉

(中国海洋大学数学科学学院, 山东 青岛 266100)

空间与时间是一切人类活动、社会事件和物理现象的两个基本维度。随着观测、实验和数值模拟技术的发展,时空数据的来源已经十分丰富,处理具有时空依赖性的观测数据已成为地球科学、环境科学、生物学和医学等研究领域的一个关注点。时空数据的一个重要特征是不同变量间的关系在空间与时间上可能存在着显著的变化。经典的回归模型由于假定回归系数为常数,所以无法捕捉响应变量与协变量之间的回归关系在时空域上复杂的变化特征。

变系数回归模型为刻画时空变量的关系提供了可能。早期的变系数回归模型主要是用于估计响应变量与协变量之间的回归关系在空间上的变化特征。例如,Brunsdon等[1]提出的地理加权回归(Geographically weighted regression, GWR)模型是一种用于解决空间非平稳性的空间统计方法,允许响应变量和协变量之间的关系随着地理位置的变化而变化。GWR模型基于局部回归的思想,在估计某个空间点上的回归系数时,利用其邻近空间点上的观测信息,并按照距离远近施以不同的权重来进行估计。在过去20年中,GWR模型被广泛用于地球科学、农业和社会经济等领域。Huang B等和Fotheringham等[2-3]通过将权重函数从空间推广至时空域,构建了时空地理加权回归模型(Geographically and temporally weighted regression, GTWR),实现了对随时空变化的回归系数的估计。Gelfand等[4]提出的空间变系数(Spatially varying coefficient, SVC)模型将回归系数看作是一个多元空间高斯过程的实现,并利用贝叶斯的方法进行估计。Song等[5]对SVC模型进行了拓展,建立了时空变系数(Spatiotemporally varying coefficients, STVC)模型。

GTWR和STVC模型都假定回归系数随时空连续变化。然而,在很多实际应用中回归系数会呈现出团状结构,即回归系数可能会在时空域的某些子区域内保持相对稳定,而在不同子区域间的界面上产生突变。例如,社会经济活动中,社区房产价格和教育水平间的关系可能会受到政府宏观政策的影响在时间上发生突变;海洋学研究中,海水物理化学性质间的关系在同一水团内部保持相对均匀,但在不同水团的边界上产生显著变化。

针对回归系数在空间上的团状结构,Li和Sang[6]提出了空间团状系数回归(Spatially clustered coefficient, SCC)模型。SCC模型结合了统计学中的变量选择理论和图论中的最小生成树理论,通过对最小生成树所连接的空间点上的回归系数的差异实施惩罚来捕捉回归系数在空间上的团状结构。本文将SCC模型拓展至时空域,提出一种可以估计在时空域上呈团状分布的回归系数模型,即时空团状系数回归(Spatio-temporally clustered coefficient, STCC)模型。STCC模型通过对时空域内相邻点上的回归系数进行惩罚,来促进时空邻近回归系数之间的同质性。

1 STCC模型介绍

假设一组时空观测数据{(x(si,tj),y(si,tj)),i=1,…,n,j=1,…,m},其中s1,…,sn∈Rd(d≥2)代表空间位置,t1,…,tj∈R代表时间位置,x(si,tj)=(x1(si,tj),…,xp(si,tj))T为p维解释变量,y(si,tj)为响应变量。考虑时空变系数线性回归

(1)

式中:βk(si,tj)是随时空变化的回归系数;ε(si,tj)是均值为0、方差为σ2的独立同分布随机噪声。当xp(si,tj)≡1时,βp(si,tj)代表随时空变化的截距。

假定在同一时空位置仅有一次观测,则可将式(1)写作矩阵形式

y=Xβ+ε。

(2)

式中:β=(β1,…,βp)T;βk=(βk(s1,t1),…,βk(sn,t1),…,βk(s1,tm),…,βk(sn,tm));(n·m)×(n·m·p)维设计矩阵X=[diag(X1),…,diag(Xp)],Xk=(xk(s1,t1),…,xk(sn,t1),…,xk(s1,tm),…,xk(sn,tm))T。

对于p>1,n·m·p>n·m。因此,无法直接使用普通最小二乘拟合来估计式(2)中β的值,故需将其正则化。假定时空域中相邻位置的β倾向于一致,则可通过最小化以下目标函数来估计β:

(3)

式中:P是一个惩罚矩阵,用于促使相邻位置回归系数之间的同质性;λ是惩罚参数,决定惩罚的强度。接下来将讨论P和λ具体的选择方法。

1.1 选择惩罚矩阵P

我们分别对空间上和时间上的相邻点进行惩罚。在空间上,我们采用与SCC模型一致的空间惩罚矩阵,即通过最小生成树将同一时刻的不同空间位置连接,被连接的两个点被认为是邻近的,对其回归系数间的差异进行惩罚。在时间上,惩罚可采用不同的形式,如对时空位置(si,tj),j≠1,将其与(si′,tj-1)间的回归系数差异进行惩罚,其中si′为si的空间位置相邻点。此处我们采用最简单的形式,即令i′=i。即

(4)

式中:H为(n-1)×n维的空间惩罚矩阵;O为(n-1)×n维的零矩阵;In为n×n维的单位矩阵。τ∈[0,∞)为时空惩罚比,用于控制时间惩罚与空间惩罚的相对大小。

当τ=0时,STCC模型相当于使用SCC模型对每个时刻的回归系数进行估计;而当τ→∞时,STCC模型相当于使用Fused LASSO模型[7]对每个空间点上的回归系数进行估计。对于一般的τ>0,惩罚矩阵P同时对空间和时间上的相邻点的回归系数差异进行惩罚。为同时促使回归系数在空间和时间上的同质性,形成时空域上的团状结构,我们取τ=1。

1.2 选择惩罚参数λ

在STCC模型中,惩罚参数控制了回归系数在时空域中的同质性程度。当λ→∞时,模型的回归系数为常数,即将整个时空域视为一个团;当λ→0时,STCC模型退化为逐点最小二乘拟合,即每个时空观测点单独成团。可采用广义交叉验证、AIC、BIC、EBIC等模型选择准则来确定最优的λ值。与Li和Sang[6]相同,我们这里采用BIC准则。

2 计算方法

为了便于表示,将针对p个解释变量的惩罚矩阵P合写为一个矩阵

(5)

式中:P=n·m·p,Q=(n-1)·m·p+n·(m-1)·p。此时式(3)可以改写为

(6)

式(6)可看作是一种特殊的Fused LASSO形式,这意味着可以使用线性交替方向乘子法(Linear alternating direction method of multipliers, LADMM)算法来估计β。

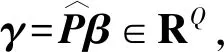
(7)

式(7)的增广拉格朗日函数是

(8)

第一,对迭代中β子问题进行求解。

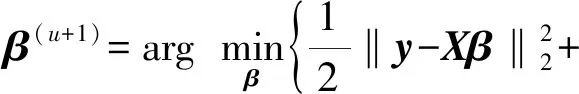
(9)

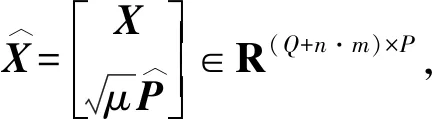
(10)

(11)

第二,对迭代中γ子问题进行求解。

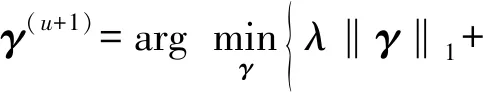
(12)

式中soft为软阈值函数,软阈值函数可由下式定义:

soft(a,b)=sign(a)·max{0,|a|-b}。

(13)

式中sign为符号函数。

第三,对迭代中α子问题进行求解。

(14)

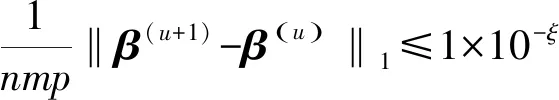
3 数值仿真研究

本节通过数值仿真实验来探究STCC方法在不同情形下的稳健性。为了便于展示,我们考虑二维空间(即d=2)中的三种情形。在前两种情形中,回归系数均在时空域中呈团状结构,第三种情形模拟了随时空连续变化的回归系数,用以探究STCC方法的灵活性。

在[0,1]×[0,1]的正方形区域中随机生成n个空间位置,每个空间位置选取8个等间隔的时间节点。取n=250,n=500,n=1 000分别对应观测样本数的少、中、多三种不同情况。时空位置确定后,响应变量y与预测变量x1和x2间的关系由以下公式刻画:

y(si,tj)=x1(si,tj)β1(si,tj)+
x2(si,tj)β2(si,tj)+β3(si,tj)+ε(si,tj)。

(15)

式中:β1(si,tj)和β2(si,tj)为随时空变化的回归系数;ε(si,tj)～N(0,σ2)独立同分布,令σ=0.1,0.2,0.4,分别对应信噪比强度的高、中、低的情况。

对于时空数据,x1和x2通常具有明显的时空结构。为了模拟这种特征,我们仿照Li和Sang[6],引入均值为0的辅助时空变量z1(si,tj)与z2(si,tj),其具有以下时空平稳协方差矩阵:

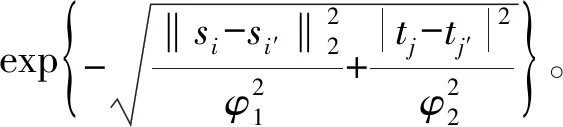
(16)

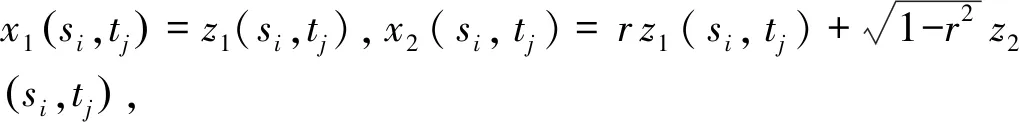
在以下分析中,我们将对比GTWR、SCC和STCC三种不同方法。对于STCC模型,式(4)中的时空惩罚比τ设为1,即对时空惩罚是同等力度的。在LADMM算法中,设定式(9)中的μ=1,收敛精度ξ=5。对SCC与STCC模型,惩罚参数λ采用BIC收敛准则来选取。对GTWR方法,采用指数核函数,其最佳带宽由交叉验证法选择。为了量化每种估计方法的性能,考虑估计的均方误差MSEβ,定义为

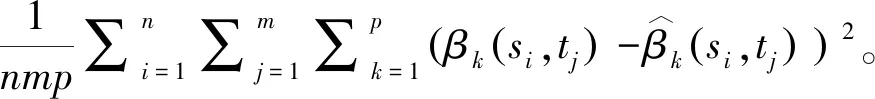
(17)

在每种情形下,我们分别比较了时空相关性、观测样本数、信噪比的变化对模型估计的影响,将100次独立数值模拟实验平均的MSEβ作为最终的MSEβ。比较时空相关性时,设定n=1 000,σ=0.1;比较观测样本数时,设定(φ1,φ2)=(0.3,4.2),σ=0.1;比较信噪比时,设定(φ1,φ2)=(0.3,4.2),n=500。

3.1 情形1

情形1模拟的是团状结构的融合过程,即空间中的两个相邻团在某时间点后合二为一,新团的性质与之前的两个团皆不相同(见图1)。β1,β2,β3分别在时间节点t=2,4,6后发生融合。表1比较了情形1下三种方法的MSEβ。STCC和SCC的估计效果明显优于GTWR,特别是样本观测数多、信噪比高、时空相关性强时,STCC和SCC的MSEβ只有GTWR方法的1/10左右。此外,对任意程度的时空相关性、观测样本数、信噪比,STCC的MSEβ均小于SCC的MSEβ。综上所述,STCC的估计效果最优。

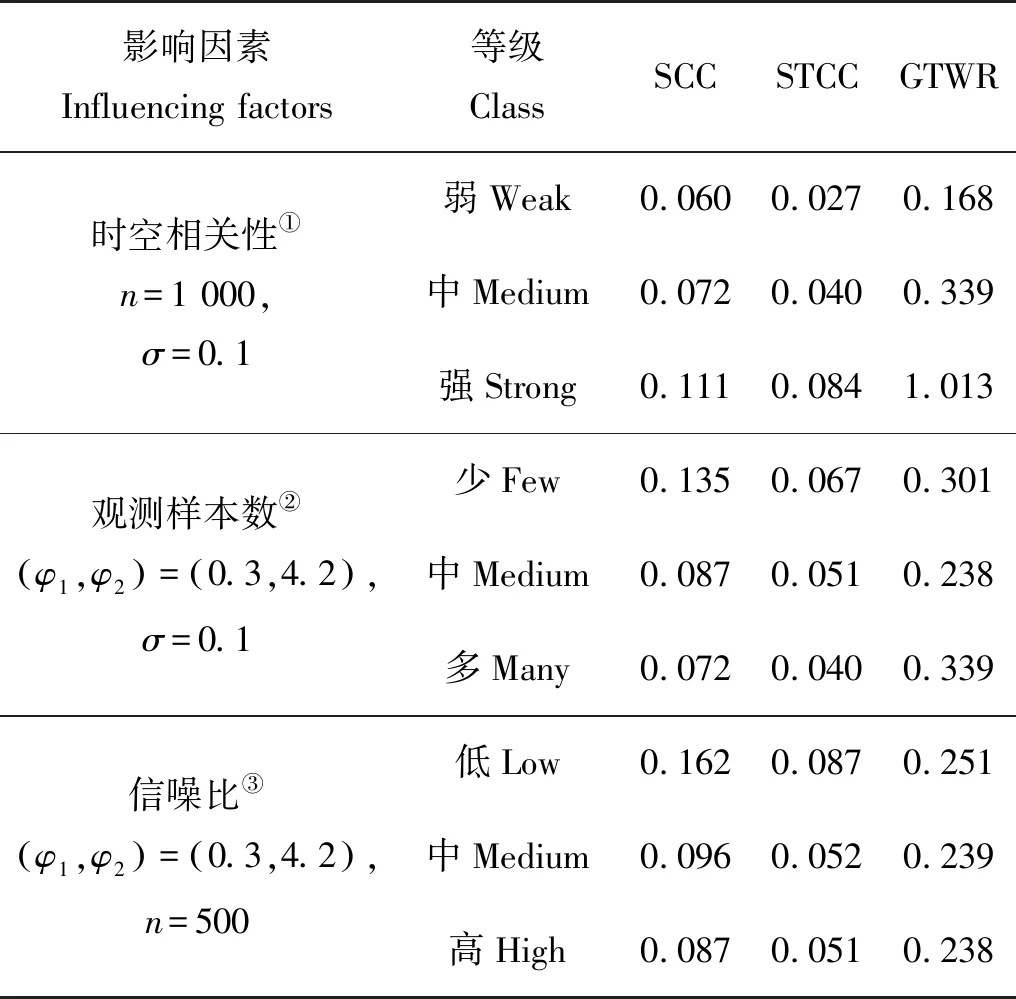
表1 情形1下SCC、STCC和GTWR方法的100次数值模拟实验的平均MSEβ

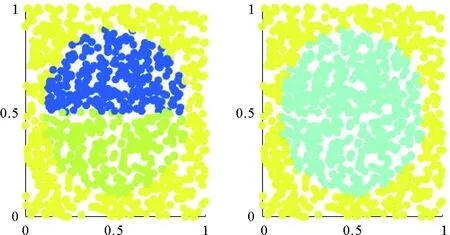
(横轴与纵轴为[0,1]×[0,1]的正方形的两个维度,无量纲。The horizontal and vertical axes are two dimensions of the [0,1]×[0,1] square region, dimensionless.)

3.2 情形2

情形2模拟的是团状结构的形变过程,即空间中的某个团在某时间点后形状发生变化,但性质保持不变(见图2)。β1,β2,β3分别在时间节点t=2,4,6后发生形变。表2比较了情形2下三种方法的MSEβ。与情形1类似,STCC的MSEβ最小,GTWR的MSEβ最大。

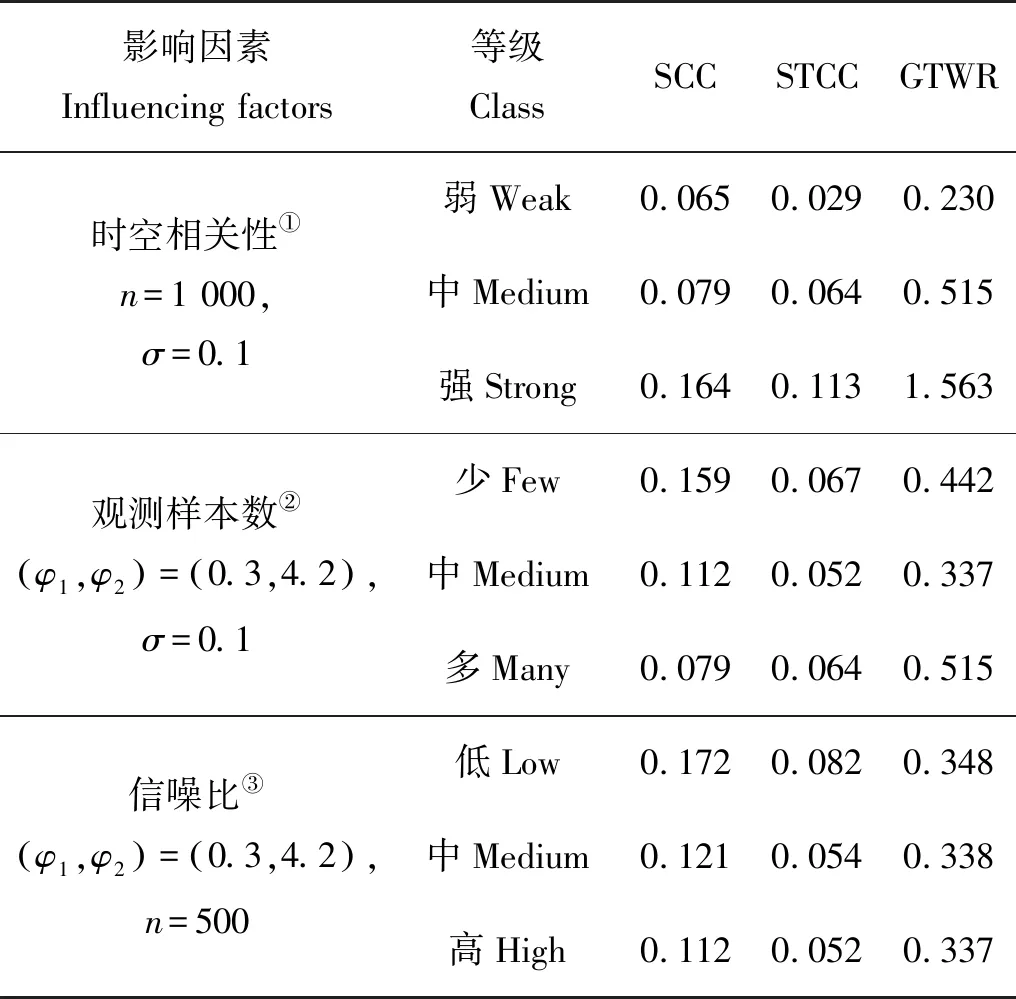
表2 情形2下SCC、STCC和GTWR方法的100次数值模拟实验的平均MSEβ

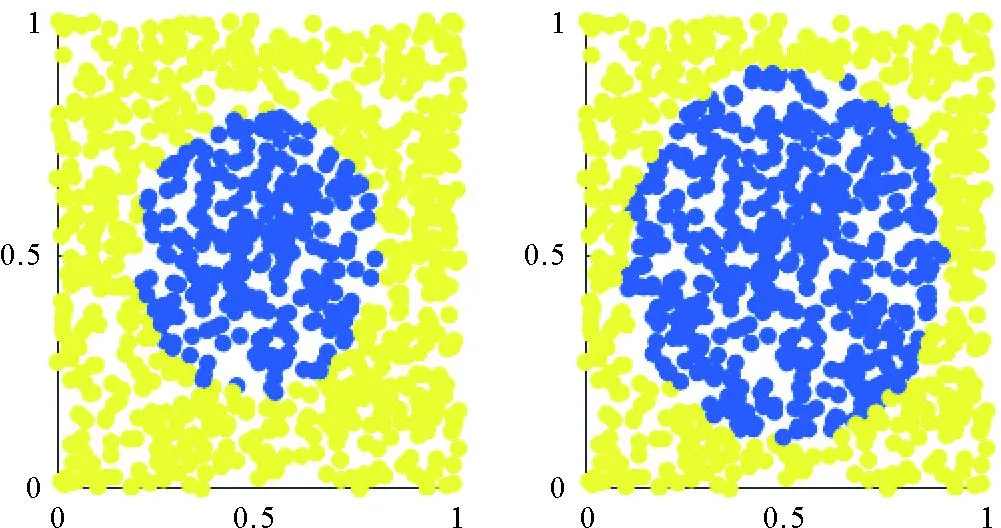
(横轴与纵轴为[0,1]×[0,1]的正方形的两个维度,无量纲。The horizontal and vertical axes are two dimensions of the [0,1]×[0,1] square region, dimensionless.)

3.3 情形3

与情形1与情形2不同,本情形考虑的是回归系数在时空上连续变化的情况,示意图见图3。表3比较了情形3下三种方法的MSEβ。在各种条件下,SCC的MSEβ均为最小。STCC和GTWR的相对优劣依赖于时空相关性、样本数量和信噪比。在高时空相关性、小样本和低信噪比条件下,STCC的MSEβ小于GTWR的MSEβ。

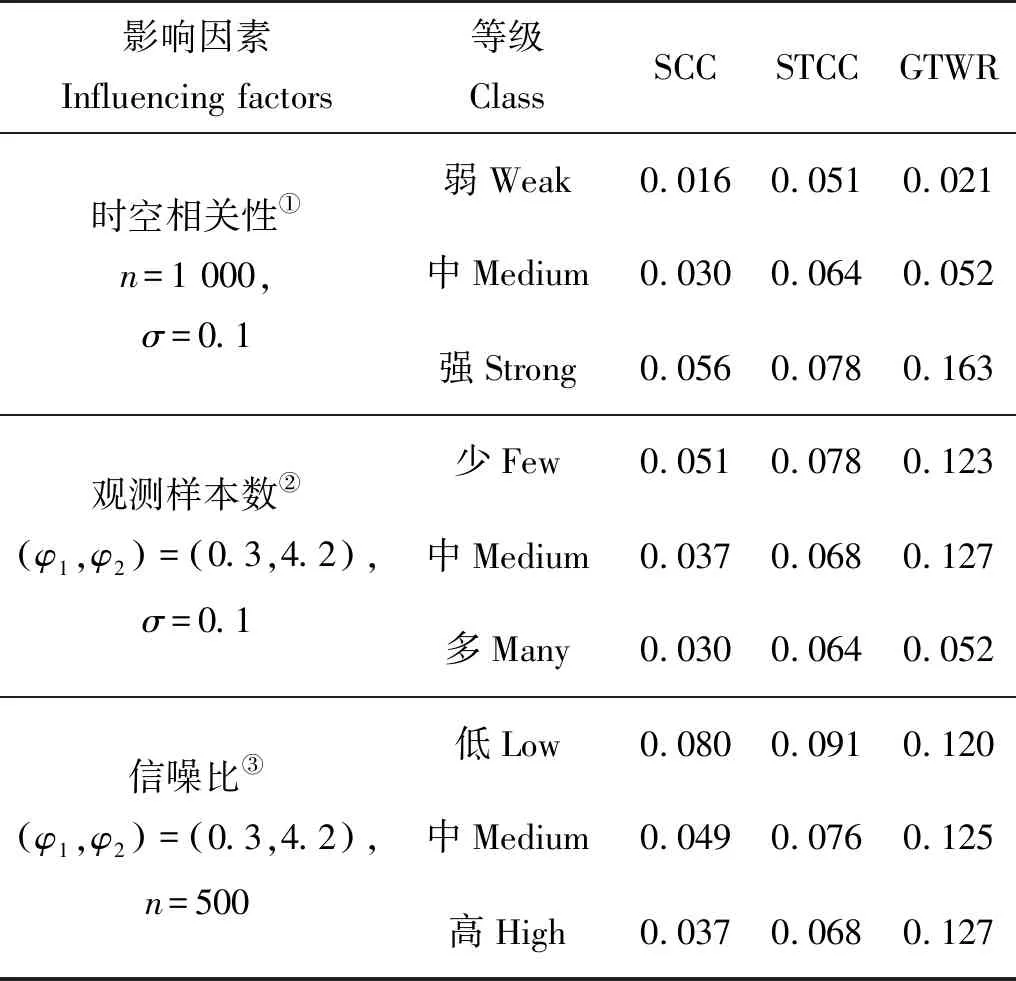
表3 情形3下SCC、STCC和GTWR方法的100次数值模拟实验的平均MSEβ

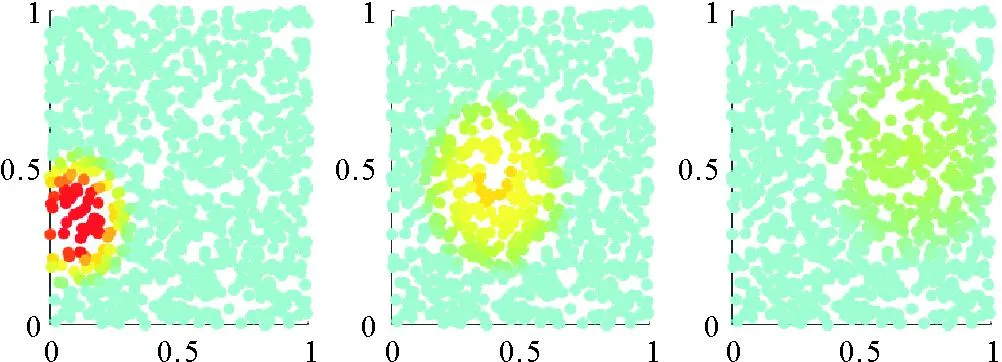
(横轴与纵轴为[0,1]×[0,1]的正方形的两个维度,无量纲。The horizontal and vertical axes are two dimensions of the [0,1]×[0,1] square region, dimensionless.)

3.4 仿真结果分析

数值仿真研究结果表明:当回归系数在时空上呈现团状结构时,STCC能够较好的捕捉到回归系数的时空结构,估计误差比GTWR小得多,也优于SCC。当回归系数在时空上连续变化时,SCC的估计效果最优,STCC和GTWR估计效果整体相当。这说明了STCC具有较强的稳健性和自适应能力。

4 海洋时空断面数据分析

4.1 数据集介绍

本节使用STCC方法估计大西洋25°W断面的温度-盐度关系,据此来检测南极中层水。南极中层水在南半球的高中纬度地区形成,在大西洋经向翻转环流影响下向北移动,对地球的气候系统有重要影响。对南极中层水范围的了解有助于推断大西洋经向翻转环流的强度。与其他水体不同,南极中层水的特点是温度-盐度关系为负,因此可以从温度-盐度关系中识别南极中层水。温度和盐度数据从美国国家海洋和大气管理局发布的2018年世界海洋图集(WOA2018)中取得。为了便于分析,本文选取了沿25°W,在60°S和60°N之间的一个温度和盐度的经线段进行研究,随机选取了共10 000个地点的温度和盐度测量值。

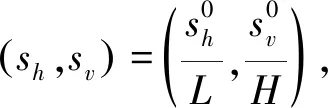
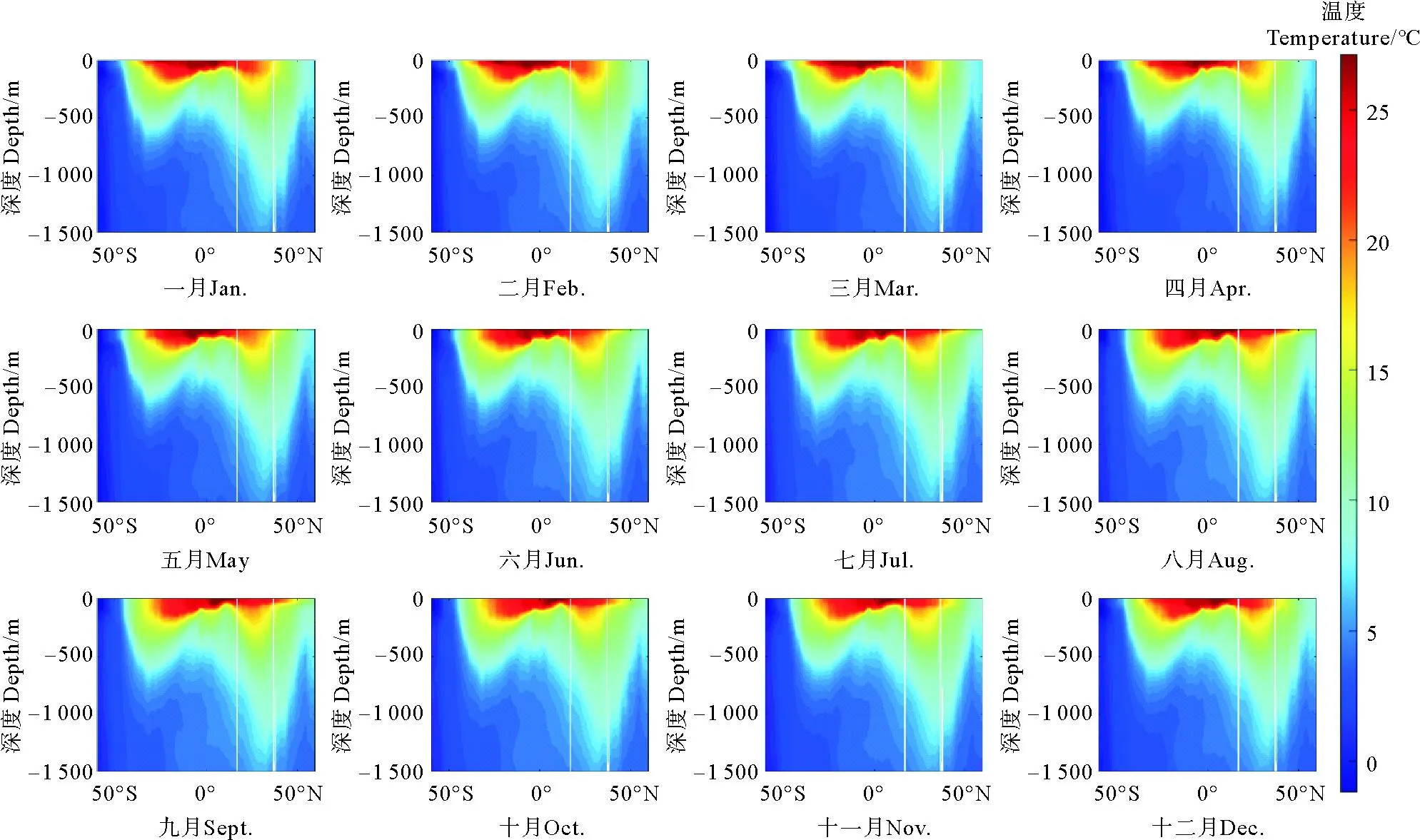
图4 25°W断面每月温度分布图Fig.4 Temperature distribution map along 25°W per month

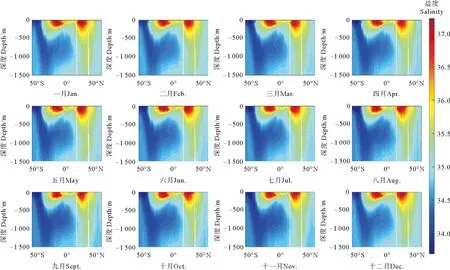
图5 25°W断面每月盐度分布图Fig.5 Salinity distribution map along 25°W per month

4.2 估计结果及分析

为了检测温度-盐度关系的时空结构,建立如下的回归模型:

S(si,tj)=T(si,tj)β1(si,tj)+
β0(si,tj)+ε(si,tj)。

(18)

式中:响应变量S(si,tj)表示时空位置(si,tj)的盐度;T(si,tj)表示温度;回归系数β1(si,tj)衡量了温度-盐度关系;β0(si,tj)是截距项。将S与T进行无量纲化,即分别除以自身标准差σS,σT,得到S′与T′,建立回归关系

S′(si,tj)=T′(si,tj)η1(si,tj)+
η0(si,tj)+ε′(si,tj)。

(19)

不难得出η与β之间的关系为

β1(si,tj)=η1(si,tj)σS/σT,

β0(si,tj)=η0(si,tj)σS。

(20)

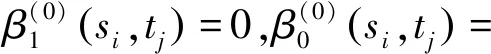
使用STCC、SCC和GTWR模型估计出的β1的系数分布(见图6、图7和图8)存在差异。STCC估计得到的β1在空间上的分布比较光滑,其识别出的负温度-盐度关系区域包括公认的南极中层水的生成地,以及被认为与南极中层水有关的低盐水舌[9]。尽管SCC识别出的负温度-盐度关系区域与STCC类似,但是其估计得到的β1在某些区域表现出网格状结构。这种网格状结构与实际海洋中的温度-盐度关系结构不符,更可能是方法本身的不足所造成的虚假结构。GTWR模型的估计结果有大量零散分布的异常值,与真实海洋明显不符。因此,相比于GTWR与SCC,STCC估计得到的β1更好地反映了实际海洋中的温度-盐度关系。

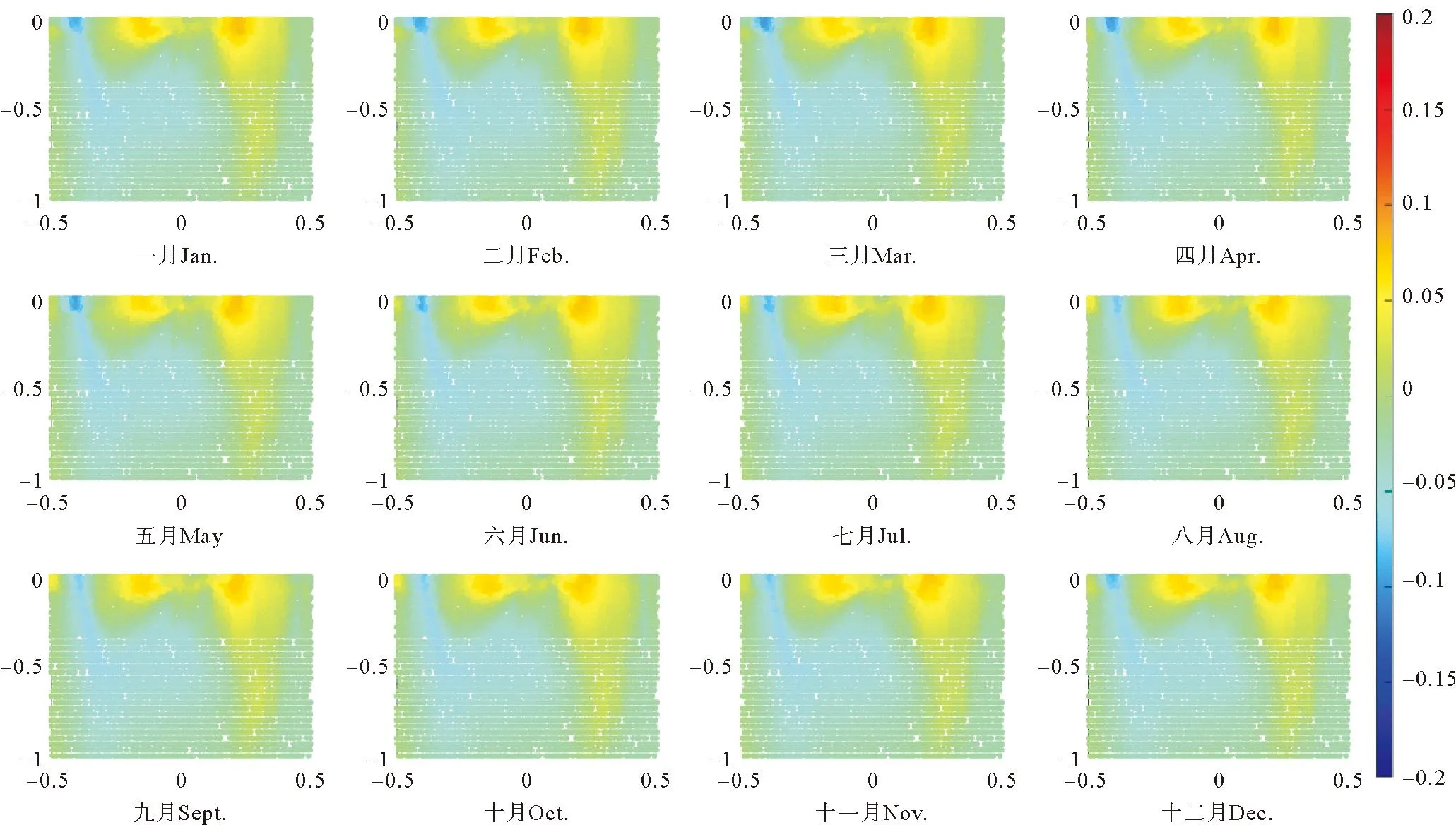
(横轴和纵轴分别为无量纲的水平和垂直坐标,右侧图示中数字为回归系数值。The horizontal and vertical axes are nondimensional coordinates of horizontal and vertical. The numbers in the right diagram are regression coefficient values.)

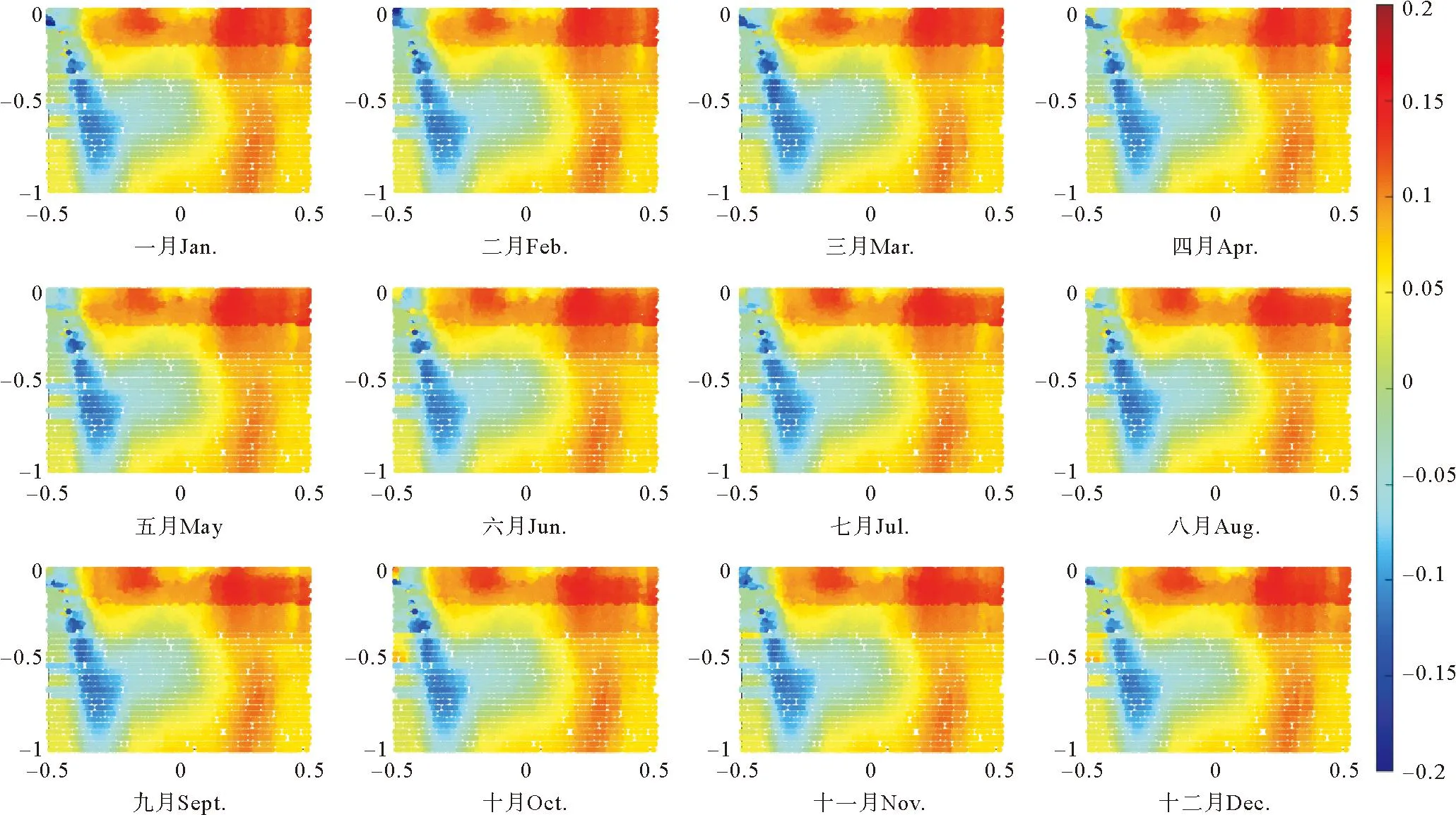
(横轴和纵轴分别为无量纲的水平和垂直坐标,右侧图示中数字为回归系数值。The horizontal and vertical axes are nondimensional coordinates of horizontal and vertical. The numbers in the right diagram are regression coefficient values.)

5 结语

本文提出了一种新的时空回归方法,该方法称为STCC方法。STCC方法可以捕获回归系数中的时空模式,特别是团状模式。基于海洋的温度、盐度观测数据,使用STCC方法检测了南极中层水的时空位置,并给出了随月份变化的大西洋25°W断面海水的温度-盐度关系。本研究识别出的负温度-盐度关系区域有助于划分南极中层水的影响范围,为海洋的其他相关研究提供参考。