某中低速磁悬浮转向机构拉杆的失稳分析

徐 阳，阳光武

（西南交通大学牵引动力国家重点试验室，四川 成都 610031）

1 引言

中低速磁悬浮列车，可利用电磁力将列车悬浮，并利用直线电机驱动，运行时速为（100～120）km。具有噪声低，线路适应性强，乘坐舒适，运行安全可靠等优点，适用于城市内近距离的交通连接［1］。

由于中低速磁悬浮列车速度较慢，所以转弯半径较小，故需要专门的转向机构使列车通过曲线。在典型的五转向架磁浮车辆中设有两套转向机构，转向机构主要由长短转臂、转向拉杆以及转轴等结构组成。

其中转向拉杆主要受到拉力的作用，所以在设计之初并没有考虑受压的情况，但是在某些情况下，拉杆需要承受一定的压力。所以这里通过理论计算，屈曲分析以及大变形分析方法对转向拉杆进行受压失稳分析。

对于杆件受压失稳，文献［2］提出了通过捕捉细长压杆失稳时的失稳点来确定压杆临界力的分析方法，结果表明，此方法所得到的失稳临界压力值大于利用欧拉公式计算的临界压力值。文献［3］通过有限元软件对细长压杆的临界压力进行数值模拟，结果表明，临界压力的数值解与理论值基本一致。文献［4］建立了压杆失稳后的弹塑性曲率与载荷的公式，求出了压杆失稳后的弹塑性数值解。文献［5］利用挠曲线近似微分方程分析了细长压杆稳定性问题，对传统的边界条件进行了修正，重新解释了以往认为临界挠度无法确定的原因。

2 失稳理论

2.1 屈曲分析理论

细长压杆临界态屈曲一般模型可表达为［6］：

式中：k2=F/EI；A、B为待定常数；F—轴向载荷；E—杆件材料的弹性模量；I—杆件截面的最小惯性矩；l—杆件长度；wAB—杆件两端的相对横向位移。

对于两端铰支的杆件，按照式（1），将边界条件w(0)=0，w(l)=0 代入方程，这里可以得到杆件的挠曲线方程：w(x)=当n=1 时的一阶屈曲方程为：，挠曲线为正弦曲线。其一阶屈曲形态，如图1（a）所示。当n=2时的二阶屈曲方程为：w(x)=Asinx，挠曲线为正弦曲线，拐点位置在x=l/2处，位于杆件中部。其二阶屈曲形态，如图1（b）所示。

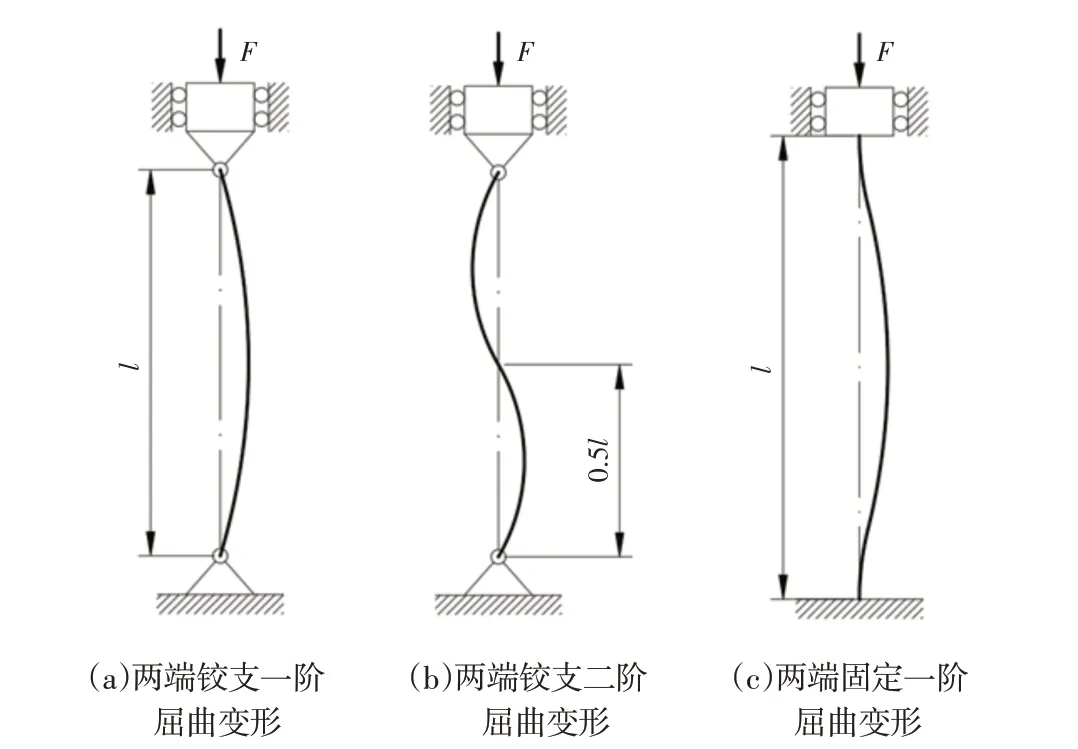
图1 杆件失稳形态Fig.1 Instability Form of Members

对于一阶屈曲形态，kl=π，可以计算出临界载荷；对于二阶屈曲形态，kl=2π，可以计算出临界载荷。可以看到，对于两端铰支的杆件，二阶屈曲临界载荷是一阶屈曲载荷的4倍。

对于两端固定的杆件，按照式（1），将边界条件w'(0)=0，w'(l)=0，w(0)=w(l)代入方程，可以得到杆件的挠曲线方程：当n=1 时的一阶屈曲方程为：w(x)=Bcosx+wAB，挠曲线为余弦曲线，此时kl=2π，可以计算得到失稳临界载荷Fcr=可以看到两端铰支的二阶屈曲临界载荷与两端固定的一阶屈曲临界载荷相等。杆件两端固定时的一阶屈曲形态，如图1（c）所示。

上述推导的不同情况下的临界载荷可以统一用欧拉公式进行描述［7］：

式中：Fcr—临界载荷；μ—压杆长度因数。

由上述公式可知，两端铰支的一阶屈曲长度因数μ为1，两端铰支的二阶屈曲和两端固定的一阶屈曲长度因数皆为0.5。

2.2 特征值屈曲分析

在数值分析中，屈曲分析经常用来分析结构在特定载荷下的稳定性和临界载荷；其中的特征值屈曲分析可以用于预测一个理想弹性结构的理论屈曲强度（分叉点）。特征值屈曲分析的公式如下所示［8］：

式中：［K］—刚度矩阵；

［S］—应力刚度矩阵；

｛ψ｝—位移特征矢量；

λ—特征值（载荷因子）。

利用上述的公式即可用数值方法求得结构的分叉点，即理论屈曲强度。

3 拉杆模型介绍

3.1 实体模型

此次计算的模型为某中低速磁悬浮列车二次系转向机构的拉杆结构。转向机构整体示意图，如图2所示。可以看到转向机构由两端的长短转臂、轴座以及转向拉杆组成。其中，X方向为纵向，Y向为横向，Z向为垂向。拉杆主体结构为空心圆柱，两端通过带有螺纹的实心导杆与拉杆头连接，拉杆头再通过铰接的方式与转臂连接。整个拉杆的长度按照两端铰接孔中心点的距离计算，为4278mm。转向拉杆的头部结构，如图3所示。拉杆的横截面，如图4所示。内径为24mm，外径为30mm。拉杆的材料为1Cr18Ni9不锈钢，不锈钢的材料参数，如表1所示。按照拉杆的形状以及材料参数，由式（2）可以计算得到拉杆的一阶屈曲临界载荷为2658.5N，二阶屈曲临界载荷为10634N。

表1 材料参数Tab.1 Material Parameters

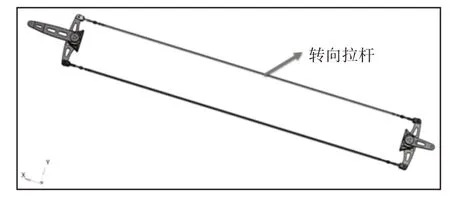
图2 转向机构Fig.2 Steering Mechani sm

图3 拉杆头部结构Fig.3 Structure of Pull Rod Head

图4 拉杆截面Fig.4 Cross Section of Tie Rod

3.2 有限元建模

对拉杆结构按照实体进行网格离散，对中间空心圆管以及圆柱体使用六面体SOLID185单元，对拉杆头处不规则的实体采用四面体SOLID185单元，网格尺寸为4mm。

然后将两端的铰接孔建立rbe2刚性单元，并在一端约束X、Y、Z的平动自由度与X、Y的转动自由度，释放Z向转动自由度；另一端约束Y、Z的平动自由度与X、Y的转动自由度，释放X向（即轴向）平动自由度和Z向转动自由度。建立的模型以及约束条件，如图5所示。

图5 模型及约束条件Fig.5 Model and Constraints

4 数值计算

4.1 特征值屈曲分析

由于屈曲分析是将结构的模态振型作为初始缺陷，然后计算结构发生相应振型变形时的分叉点，来作为理论临界失稳载荷，所以首先对转向拉杆进行模态分析，来观察杆件的失稳变形形式。杆件的前三阶模态，如图6 所示。可以看到拉杆的一阶模态是在XY平面中弯曲，二阶模态是在XZ平面中弯曲。三阶模态则是杆件在XY平面中的二阶弯曲。其中，XY平面是拉杆端部可以绕铰接点旋转的面，这时杆系的长度因素μ为1，而在二阶模态中，弯曲的XZ平面中杆件两端不能绕铰接点进行旋转，所以相对应的长度系数μ为0.5，等价于两端固定的约束条件。

图6 拉杆模态Fig.6 Mode of Tie Rod

接着进行拉杆的屈曲分析，按照之前所述的模型中，在释放X平动自由度（即轴向自由度）的一端分别施加100N、500N以及1000N的压力，进行屈曲分析计算，得到的不同载荷对应的屈曲载荷因子，如表2所示。

表2 不同载荷下拉杆屈曲载荷因子和临界压力数值解Tab.2 Numerical Solution of Buckling Load Factor and Critical Pressure of Tie Rod Under Different Loads

杆件不同阶数的屈曲变形，如图7所示。可以看到一阶屈曲变形对应一阶模态，二阶屈曲变形对应三阶模态，三阶屈曲变形对应二阶模态。

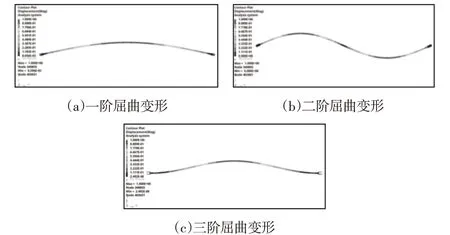
图7 屈曲分析变形Fig.7 Buckling Analysis Deformation

将不同阶数的临界屈曲载荷与屈曲变形相结合观察，可知，施加不同的载荷时，所得的屈曲载荷因子也不相同，将载荷因子乘上施加的载荷就是所需要的临界载荷，可以看到一阶模态下所计算出的临界载荷都比较接近理论计算值的2658.5N，与理论计算结果最大误差不超过1.74%，二阶模态下计算出的临界载荷基本一致，都为11135N，与理论计算值10634N的误差为与4.71%。三阶模态下计算得出的临界载荷都为10486N，与理论计算结果误差为1.4%。由于在杆件两端有实心杆以及不规则形状等的影响，故可以认为数值分析计算结果与理论值是相对应的。

4.2 大变形分析

在小变形假设前提下，在考虑平衡条件时可以不考虑物体的位置和形状的变化。但是在压杆稳定性分析中，压杆会出现明显的弯曲变形，这时的平衡方程需要相对于变形后的位置建立，并且几何关系应该包括位移的二次项，所以需要将有限元分析中的大变形分析打开，来计算压杆的临界失稳载荷。

4.2.1 两端铰支一阶弯曲

由于失稳需要给杆件一个微小扰动，所以首先在XY平面内施加Y向的扰动，来模拟长度因数μ为1时的约束情况。在拉杆的中间分别加上0.5N、0.2N、0.1N 以及0.04N 这四种不同程度的扰动来对比计算结果；然后在未约束轴向位移的一端施加3000N的轴向力，并设置多个载荷步，以便计算完成之后提取加载点的位移以及固定点的支反力。两端铰支的约束条件，如图8所示。

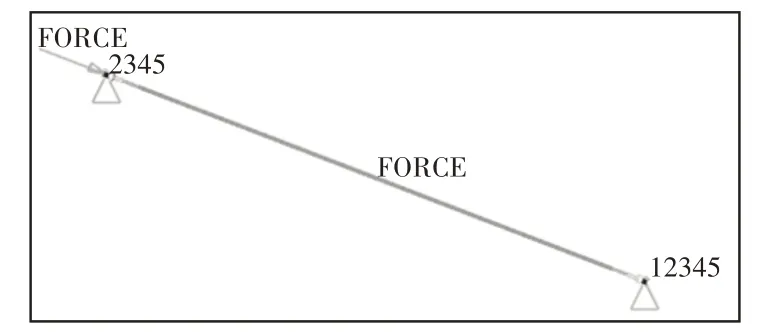
图8 两端铰支约束条件Fig.8 Constraint Conditions of Hinged Support at Both Ends

计算完成后，将提取的位移作为横轴、反力作为竖轴来画出载荷位移曲线，通过观察载荷位移曲线不再是线性变化时，就说明拉杆已经受压失稳，从而将失稳载荷与理论计算值进行对比。四种不同扰动下的载荷位移曲线，如图9所示。可以看到一开始位移和支反力是线性变化的关系，但是到了临界载荷附件的位置，曲线出现了拐点，说明压杆已经失稳，拐点处的支反力就是杆件的临界失稳载荷。

4.2.2 两端铰支二阶弯曲

然后模拟三阶模态下的压杆失稳，即二阶屈曲载荷因子下的失稳情形。在XZ平面内施加Z向的扰动，来给杆件一个中部的扰动，依旧施加0.5N、0.2N、0.1N 以及0.04N 四种扰动，前面理论计算得出临界载荷大概在10600N 左右，所以施加12000N的轴向力来进行计算。四种不同扰动下的载荷位移曲线，如图10所示。

图10 载荷位移曲线Fig.10 Load Displacement Curve

4.2.3 两端固定一阶弯曲

最后模拟长度因数为0.5时的情形，将一端的六个自由度全部约束，另一端只释放轴向自由度。然后在XZ平面内施加Z向的扰动，由于在长度因数为0.5的约束下杆件刚度较大，所以施加扰动也需要相应增大，施加载荷分为为20N、10N、5N三种。两端固定的约束条件，如图11所示。

图11 两端固定约束条件Fig.11 Fixed Constraint Conditions at Both Ends

通过计算可得到图12中三种不用扰动下的载荷位移曲线。

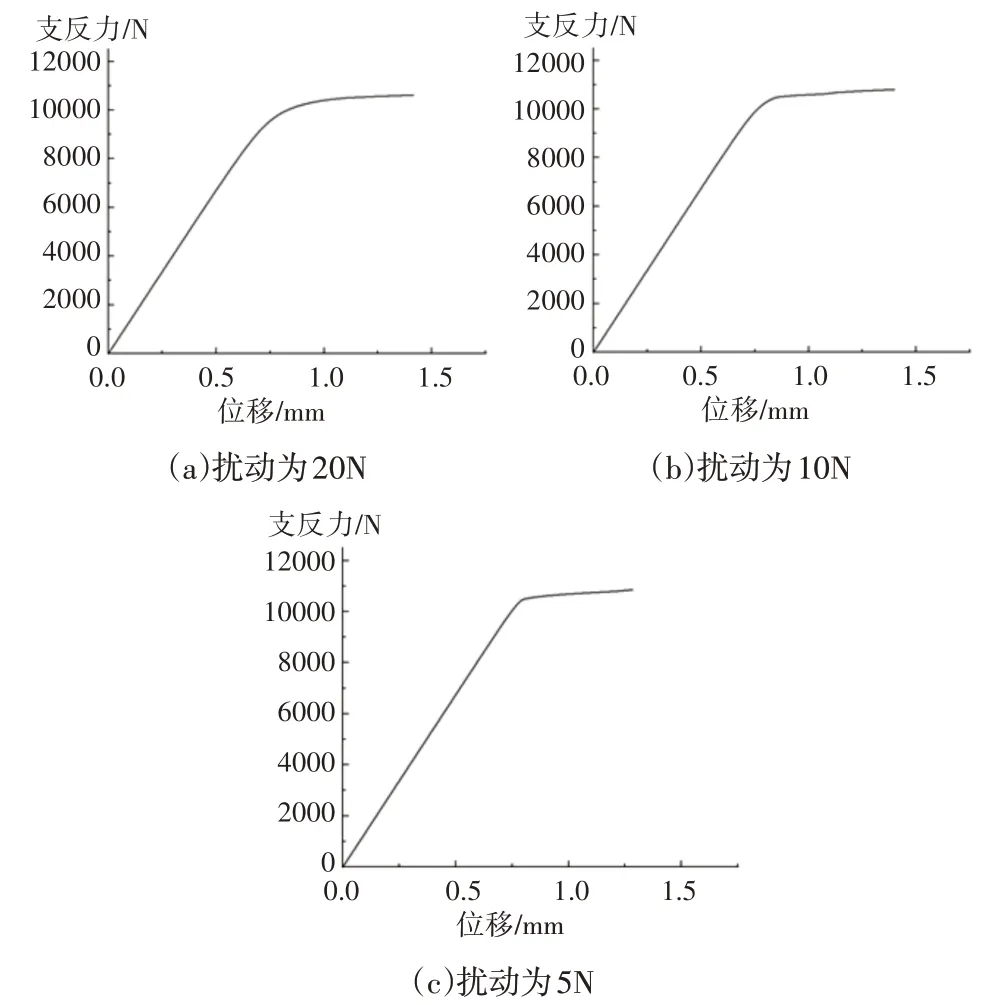
图12 载荷位移曲线Fig.12 Load Displacement Curve

由图12 所示的拐点可以知道两端固定时杆件失稳的临界载荷。不同约束不同扰动下的临界载荷仿真结果，如表3所示。可以看到中部施加的扰动越小，载荷位移曲线的拐点越明显，临界载荷越接近理论值。由上表可知，大变形计算结果与理论计算结果非常接近，说明大变形方法在分析压杆失稳时也有不错的精度，但是计算时间较长，并且需要提取位移和支反力，在便捷程度上不如特征值屈曲分析。杆件在大变形计算结果下的变形，如图13所示。可以看到与之前理论分析和屈曲分析下的变形基本一致。

表3 不同约束不同扰动下的临界载荷仿真结果Tab.3 Simulation Results of Critical Load Under Different Constraints and Disturbances

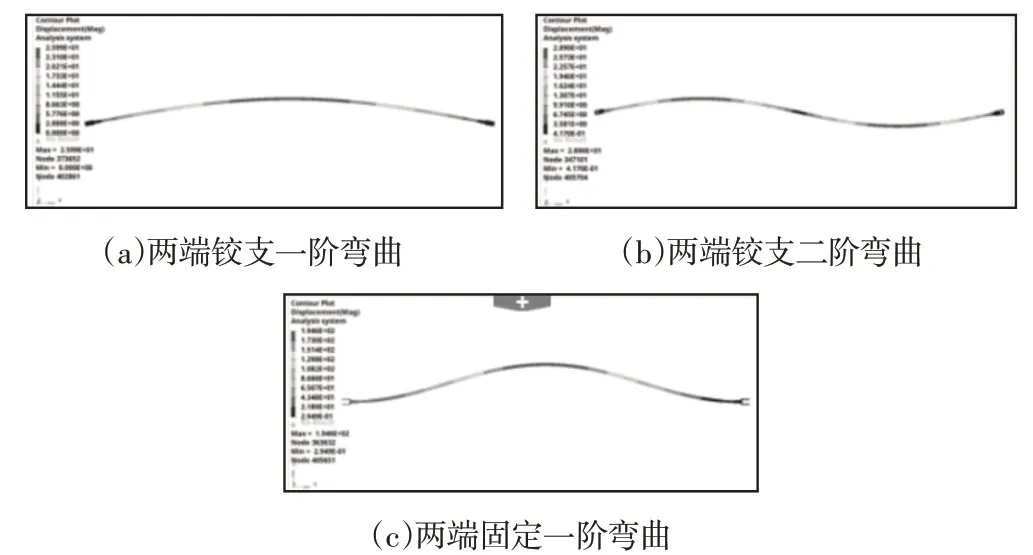
图13 大变形分析下杆件变形Fig.13 Deformation of Bar Under Large Deformation Analysis

5 结论

（1）推导了杆件两端铰接时，一阶和二阶屈曲形态的挠度曲线和临界载荷；以及两端固定下一阶屈曲的挠度曲线与临界载荷。计算得出两端铰接的一阶屈曲临界载荷为2658.5N，二阶屈曲载荷为10634N。并且两端铰接的二阶屈曲载荷与两端固定的一阶屈曲载荷相等。

（2）对磁浮转向机构的拉杆结构进行特征值屈曲分析，发现通过不同初始载荷计算所得的杆件变形与临界载荷基本一致。一阶屈曲载荷都在2620N左右，二阶屈曲载荷都为10486N，三阶屈曲载荷为11135N。

（3）在大变形分析中，不同初始扰动会对临界载荷的计算有一定的影响，扰动越小，影响越小。在扰动足够小的情况下，大变形分析得出的杆件变形结果与临界载荷和理论分析基本一致。

（4）通过理论计算，特征值屈曲分析以及大变形分析方法的三种结果对比，发现计算结果基本一致，可以认为三种计算方法都可以用于工程分析，尤其是分析某些复杂结构时，特征值屈曲分析可以很方便地计算出结构的临界失稳载荷。