带有删失函数型协变量的非参数模型的估计研究

李 响，王纯杰，卢哲昕，徐 萍

随着技术的进步，函数型数据分析在越来越多的领域中发挥着重要作用，如医学、生物学、经济学等领域.由于观测对象在试验中需要长期随访，因此，每个观测对象的生理指标的测量结果通常被记录为曲线的形式，并且由于观测对象加入试验、退出试验的时间不一致或者中途退出导致的差别、观测时间的局限性或客观条件的限制等因素的影响，人们通常不能得到完整的观测曲线.例如在医学研究中许多数据集是通过患者定期检查并记录下来，然而患者忘记检查或者医疗设备的损坏都可能产生删失函数型数据.目前对于删失函数型数据已经有学者进行了研究，例如DELAIGLE 等［1］使用曲线扩展算法对删失函数型数据进行扩展.DELAIGLE 等［2］提出使用马尔科夫链的方法对删失函数型数据进行扩展.KRAUS 等［3］提出正则化方法对不完整的函数型数据进行分类.DELAIGLE 等［4］通过计算张量级数的方法得到协方差函数并且得到近似完整的函数型数据.DESCARY等［5］对规则密集的数据提出使用矩阵补全方法重新构造协方差函数.LIN 等［6］针对删失函数型难以计算非对角线区域的信息问题，使用基函数展开的方法估计协方差函数.LIN等［7］把协方差函数分解为方差函数分量和相关函数分量来解决删失函数型的协方差函数不好估计的问题.赵志文等［8］在缺失数据下使用均值补充法、条件均值补充法研究了区间自回归模型的参数估计问题.

非参数回归模型具有回归函数形式灵活、适应性广泛的优势.FERRATY 等［9］在非参数模型下把核估计应用于函数型数据和时间序列数据.RACHDI 等［10］对非参数模型估计中的带宽选择进行研究.MOHAMMED 等［11］在非参数模型下针对函数型协变量，使用核估计方法解决鲁棒回归问题.FLORENT 等［12］提出使用k近邻方法估计非参数模型.王景乐［13］在删失指标随机缺失下研究回归函数的非参数估计.孟书宇［14］使用k近邻方法估计相依函数型非参数模型.程彦茹［15］使用k近邻方法估计随机缺失函数型非参数模型.

本文研究具有删失函数型协变量的非参数模型的估计问题.使用曲线扩展算法把删失函数型数据扩展至完整数据.通过建立非参数模型，可以得到函数型协变量对标量响应变量的预测.通过模拟研究验证该方法的有效性，并应用到肝硬化数据集.

1 模型与估计

在实验过程中人们往往以函数型数据的形式来记录试验结果，但由于各种因素不能观测到函数型数据的全部过程，因此产生删失函数型数据.假设观测数据为Xi(t) ≡Xi，i=1，…，n，每条观测数据Xi(t) 只能在部分区间Ii=[ai，bi]可被观测到，且Ii⊆I0，其中ai和bi分别表示第i个样本的左端点和右端点，I0表示完整观测的区间.例如文献［1］研究了8 岁到25 岁四个种族群体（亚洲人、黑人、西班牙人和白人）脊柱骨密度分类问题，其中对每个个体只能进行2 次到4 次的测量，只观测到部分区间内的部分函数型数据.像这种观测次数不同、观测时间不同的函数型数据，不经过处理很难建立模型.本文将介绍一种非参数的方法对删失函数型数据进行扩展，并建立非参数模型.非参数模型定义为：

式中：Yi为标量响应变量，r(⋅)为未知的非线性算子，εi为满足E(εi|Xi)=0 的随机误差，Xi为删失函数型数据.

在建立模型前需要通过曲线扩展算法把删失函数型数据进行处理.本文使用的方法为文献［8］中的函数型核估计方法，公式如下：

式中：wn，h(⋅，⋅)为权重函数，可以表示为：

式中：K(⋅)为核函数，d(⋅，⋅)为半度量，h为窗宽，在进行估计时需要对核函数、半度量和窗宽h进行选择.

2 删失函数型数据扩展算法

本文使用文献［1］提出的基于垂直距离将删失函数型数据扩展为完整函数型数据的方法.该方法具有计算快、精确度高、灵活性高、非参数等优势.具体过程为，假设观测到的样本为在区间Ishort=[ashort，bshort]上的函数型数据Xshort，其中ashort和bshort分别表示需要扩展的函数型数据的左端点和右端点，使用区间Ilong=[along，blong]⊃Ishort上的数据Xi，i=1，…，n估计Xshort未观测到的部分，并且Ishort⊂Ilong⊆其中along和blong分别表示长于数据Xshort的左端点和右端点.从bshort的右边来构造扩展数据Xext的具体算法步骤如下：

步骤1：设置对于所有的t∈[ashort，bshort]，使Xext(t)=Xshort(t)且j=1，j为扩展的次数，bext，j=bshort.

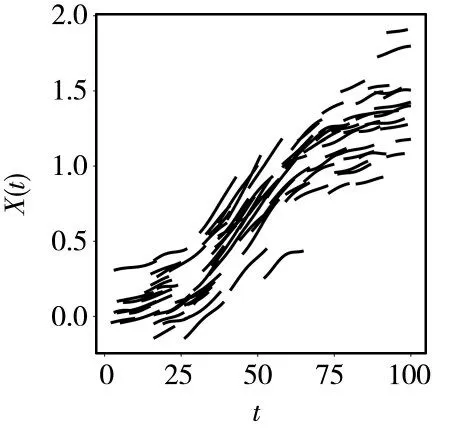
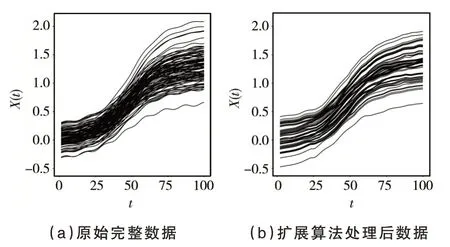
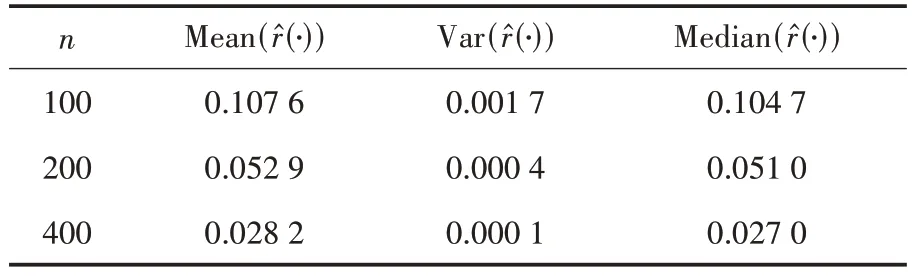
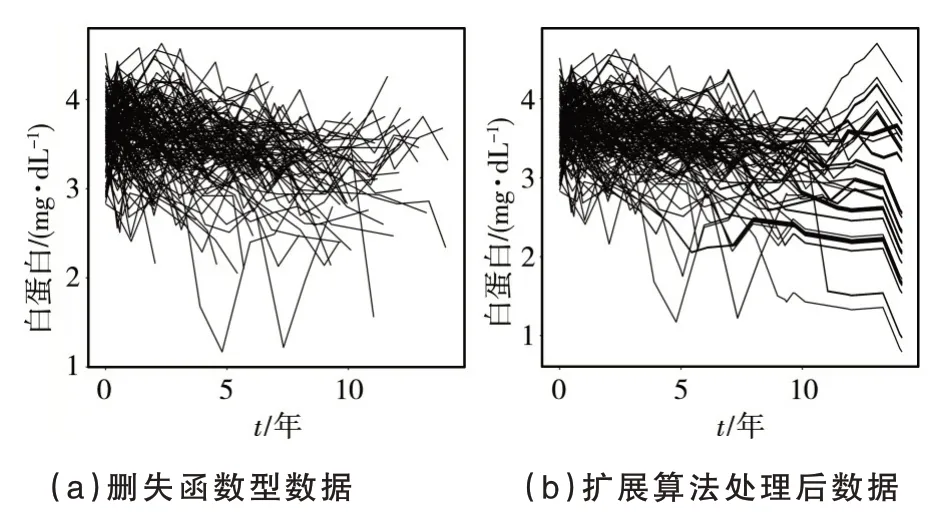
步骤2：对于j=1，2，…，重复以下步骤直到bext，j

（1）找到所有满足ai≤bext，j和bi>bext，j的函数型数据Xi，选择它们其中的一个命名为Xi*，Xi*被观测在Ii*=[ai*，bi*]，其中ai*和bi*分别表示函数型数据Xi*的左端点和右端点.

（2）扩展出的右端点bext，j+1=min(bi*，blong，bext，j+Δ)，其中Δ >0 是调优参数.

（3）对于每个t∈[bext，j，bext，j+1]，使Xext(t)=Xi*(t) −Xi*(bext，j)+Xext(bext，j).

在实践中，该算法需要在步骤2 的（2）中对调优参数Δ 进行选择，Δ 的作用是为了防止扩展过长的函数型数据片段使扩展函数型数据产生较大的误差.为了扩展数据片段Xext足够短，并且扩展的数据片段尽可能包含I0上出现的特征模态、凹凸度变化的小片段.可以设置Δ=|I0|/10，其中|I0|表示I0的长度.如果函数型数据具有快速变化的特征，Δ 可以取的更小.

算法中还需要在步骤2 的（1）中选择确定函数型数据Xi*.假设在步骤2 的（1）中有cj个满 足ai≤bext，j和bi>bext，j的函数型数据Xi，i=c1，…，cj.以下是选择函数型数据Xi*的两个方法.

方法一是在cj个碎片中随机获得函数型数据Xi*，每一个被选择的概率为pij=1/cj.当数据Xi*与来自总体的完整函数型数据的样本具有相同的主要属性时，可以使用这个方法.方法二是当一组函数型数据有明显的形状相似时，每条函数型数据的形状在局部与附近数据的形状相似.在这种情况下，可以通过选择使用最近的删失函数型数据的方式.更具体地说，假设感兴趣的是在bext，j的右边扩展数据Xext，让D(Xi，Xext；bext，j) 表 示Xi和Xext在点bext，j的距离.删失函数型数据的形状取决于它们局部垂直轴上的位置距离，让D(Xi，Xext；bext，j)=|Xi(bext，j)−Xext(bext，j)|，可以得到

同样的算法可以应用在函数型数据的左侧，通过与上面相同的方式从右向左每次扩展一小段.使用这种非参数的方法可以把删失函数型数据扩展为完整的函数型数据.

3 数值模拟

下面将通过数值模拟来验证文中所给模型与算法的可行性.定义非参数模型为：

设置εi～N(0，1)，函数型协变量为：

设置每条删失函数型数据只有在区间Ii=[Ai，Bi]上可以被观测到，其中Ai=[Ui]，Bi=min(Ai+[Vi]，100)，Ui～U[1，95]，Vi～U[7，15].上述设置模拟100 个删失函数型样本数据图如图1 所示.

图1 删失函数型数据

图1 中随机生成的100 个删失函数型数据原始完整数据与扩展算法处理后数据的对比图如图2 所示.使用垂直距离最小的方法将删失函数型数据尽可能表现出完整数据的特征，其中图2（a）为原始完整数据，图2（b）为使用曲线扩展算法补充后的数据，设置调优参数Δ=10.

图2 删失函数型数据原始完整数据与扩展算法处理后数据对比图

从图2 可以看出，使用该算法处理过的函数型数据可以近似地表现出原始函数型数据的特征.

在估计非参数模型时，选择半度量为

使用正态核函数和Nadaraya−Watson 类型的窗宽并且通过广义交叉验证程序选择最优窗宽为s=2.通过使用计算的均方误差的均值、中位数、方差对进行评价的均方误差表示为：

在上述设置下循环200 次，样本量分别为100、200、400，非线性算子的均方误差的均值（Mean()）、方 差（Var()）、中位数（Median()）评价指标如表1 所示.

表1 非线性算子均方误差的均值、方差、中位数

表1 非线性算子均方误差的均值、方差、中位数

4 实例分析

下面采用非参数模型对原发性胆汁肝硬化数据进行分析，由于不可控制的因素，所以每位患者的观测时间和观测次数都不同.本实例使用观测样本n=150 进行建模，研究白蛋白对血清胆红素的影响.设置调优参数Δ=1.5，使得删失指标白蛋白扩展至区间[0，14].

设置模型血清胆红素为响应变量Yi，i=1，…，150，白蛋白为函数型协变量且Yi=r(Xi)+εi，i=1，…，150.

在估计时采用半度量d2(Xi，Xj)=采用正态核函数和Nadaraya−Watson 类型的窗宽h，并通过广义交叉验证得分来进行选择最优窗宽.具体如图3所示.

图3 删失函数型数据与使用扩展算法处理后数据对比图

从图3 可以看出，肝硬化患者随着患病时间的延长，白蛋白会呈现下降趋势.

图4 的分布情况

5 结语

本文通过曲线扩展算法可以将删失函数型数据扩展至完整函数型数据，在建模时避免了删失函数型数据对模型的影响.通过对非参数模型中非参数算子的估计，验证估计值的相合性和稳定性.本文通过模拟数据和实例数据验证曲线扩展算法的实用性和准确性.

在曲线扩展实践中，当样本量n很小时，曲线会扩展到越来越大的区间，误差也会变大，所以曲线扩展算法样本量不能太小，并且在算法中需要曲线Xi，i=1，…，n覆盖I0大部分区间，如果在I0出现数据曲线没有覆盖到的地方，程序将无法运行.如果Xi在某一小部分区间删失的数据比较少，在数据扩展时会将大量的扩展数据集中使得误差变大，这也是后续要改进的问题.在曲线扩展中需要对参数Δ 进行选取，如果参数Δ 过大会使扩展后的曲线不能展示出I0上曲线的特征；如果参数Δ 过小首先会出现的问题是影响数据曲线整体的走势形态，其次是会极大增加不必要的计算量，运行速度降低.因此，调优参数Δ 的精确选取有待进一步研究.