小学生统计推理能力表现的实证研究
董瑶瑶,刘 坚
小学生统计推理能力表现的实证研究
董瑶瑶1,2,刘 坚1,2
(1.北京师范大学 中国基础教育质量监测协同创新中心,北京 100875;2.北京师范大学 中国教育创新研究院,广东 珠海 519087)
发展小学生统计推理能力有助于促进学生养成“用数据说话”的理性精神,契合了大数据时代对现代公民的素养要求.对此,采取混合研究方法,以一所普通公办小学的321名六年级学生为研究对象,基于统计推理能力的评价量规来开展表现性评价,刻画了学生统计推理的总体表现及典型表现特征.结果显示:在总体表现上,近九成六年级学生的统计推理能力处于单一结构水平和多元结构水平,其中超过五成的学生处于单一结构水平,少数学生仍处于前结构水平,极少数能达关联水平.在具体表现特征上:86.0%的六年级学生能推测数据之外的信息;90.1%的六年级能运用数据作为证据来初步解释推测;32.1%的学生能真正反思到推测的不确定性;在3个指标上,学生存在不同的作答策略和学习迷思.由此,通过实现评价框架、测试题、评分标准的有机统一,构建了统计推理能力的评价体系,为推动学生的统计推理能力发展,以及数据意识和推理意识的培养提供了基础.
小学;统计推理;量规;测评;SOLO;数据意识;推理意识
1 问题提出
统计推理能力(Statistical Reasoning Ability)强调“用数据说话”,是现代公民需具备的重要素养[1],其核心内涵为运用数据在不确定问题中做出理性判断和决策.统计推理在经济、政治和个人生活中发挥着重要作用.例如,在个体日常生活中,彩票购买、炒股、房价预测、市场菜价评估等均需基于数据做出判断.这种基于数据做出理性判断已成为新型决策思维方式.在此背景下,培养学生的统计推理能力得到了广泛关注.如国际经济合作与发展组织指出:“学生作为未来公民应该熟悉大数据的性质,并能在变化和不确定的情境中做出明智的决策.”[2]中国新出版的《义务教育数学课程标准(2022年版)》将“数据意识”作为小学数学核心素养,提出“会用数据的分析结果解释和预测不确定现象,形成合理的判断或决策”[3].可见数据意识的内涵和统计推理紧密相连,充分体现了新课标对小学生统计推理能力的重视.然而,从统计推理教学现状上看,统计课程本身处在中国小学数学课程中的“弱势”地位[4],统计推理的教学对小学数学教师而言也更具挑战性[5].在日常的课堂活动中,“数据”被视为“数”而不是“情境中的数”.统计教学被当作“数与代数”领域的教学[6],统计的教学变成了“确定性的教学”,这同“变”中寻找“不变”的统计推理教学理念背道而驰.尽管中国已有研究探索了小学生数据分析观念和统计思维的发展水平和表现特征[4-8],也有研究探索了国外统计推理的测评案例[9],但缺乏对中国小学生统计推理表现水平的实证研究.对此,只有明确了小学生的统计推理有哪些具体的行为表现,才有望帮助教师了解统计推理和学生统计推理的进阶策略.
已有研究对统计推理内涵、评价指标、水平划分进行了探索.在统计推理的内涵研究上,第一种观点基于统计概念来定义统计推理,侧重于以知识概念为核心,认为统计推理能解释统计的过程和结果[10-11];第二种观点认为统计推理是做出统计推断的推理过程,突出了统计推断的核心作用,强调了推理是一种认知过程[12-14];第三种观点以结论的不确定性为标识,认为统计推理是一种合情推理,强调用归纳的方法来探索和发现新的数据模式[15].不同研究者对统计推理的概念解读都体现了“对不确定问题做出决策”的内涵.正如PISA 2021所强调的那样,统计推理是要让学生在“不确定”的现实情境中挖掘数据模式,发挥统计服务于决策的实际作用[2].相比之下,第二种观点既体现了推理过程,又充分考虑了统计的不确定性.结合小学生特征,研究从该视角出发,将统计推理的概念界定为:“学生能运用已有数据对统计中的不确定性问题做出合理推测的推理过程.”
关于统计推理的评价指标,在早期研究中,研究者大多基于特定的统计概念或数据处理过程来构建统计推理的评价指标[16-17].随着国际统计教育研究的发展,研究者越来越关注在中小学领域培养学生的非正式统计推断能力,出现以推断为核心的评价框架[12-13,18].如Makar和Rubin将统计推理视为得出推断的思维过程,提出了三维理论框架: ①概括数据之外信息——对超出数据本身的总体做出推断,这是一种推测性主张;②把数据作为证据——结合情境,以统计数据作为证据来阐述结论;③运用概率语言——运用概率语言表达和阐明推断的不确定性.该框架进一步明晰了统计推理的认知要素,强调学生的数据意识,得到许多国际研究者的认可和应用.关于统计推理的水平划分,部分研究基于SOLO分类理论开发了相关的水平模型或评价量规.如Goss基于SOLO分类理论,针对变异性的运用、情境的运用、确定性和论证这3个维度分别构建了前结构水平、单一结构水平、多元结构水平、关联水平,由此分析六~八年级学生得出统计推断的推理过程[19].除了基于SOLO分类理论,其它研究也对学生统计推理的表现水平做了分析[20].纵观已有研究进展,一些研究者多在课堂研究或设计研究中以前后测的形式来评价学生统计推理能力,但这一类评价工具很难说是真正在考查学生的统计推理能力这一构念.
综上,研究通过对Makar和Rubin三维理论框架本土化,形成小学生统计推理能力评价指标,而后基于SOLO分类理论为评价指标划分学生表现水平,开发小学生统计推理能力评价量规.基于此,先从宏观层面总体描述小学生统计推理能力的表现水平,再从微观层面深度刻画不同水平学生的表现案例,以期为教师识别、评价、提升小学生统计推理能力提供借鉴,从而推动小学生数据意识和推理意识的培养.
2 研究设计
2.1 研究对象
以小学教育终端的六年级学生为例,采取方便抽样和整群抽样,在中国B市郊区选取了1所中等办学水平的公办小学,共9个班级的322名六年级学生参加测试.有效样本量为321.其中,男生165名(51.4%),女生156名(48.6%).
2.2 研究工具
2.2.1 统计推理能力评价量规
研究开发了由“3个评价指标×4个评价等级”构成的小学生统计推理能力评价量规(见表1),该量规内容也充分体现了对小学生数据意识发展的要求.首先,基于Makar和Rubin的统计推理三维理论框架,经文献分析、专家访谈后构建了统计推理能力的3个评价指标.其次,结合SOLO分类理论,通过文献分析,针对统计推理能力的3个评价指标分别初步构建“前结构水平、单一结构水平、多元结构水平、关联水平”4个评价等级.然后,经过专家访谈、6位学生出声思维、第一轮小规模预测试、第二轮大规模预测试等多轮迭代,在学生的思维过程证据和专家认可(含统计教育研究领域专家、小学数学教育实践专家)的基础上,该套评价量规得以最终确立.
该套评价量规的开发过程充分基于学生实证证据,研究在此基础上,关注学生的思维过程和建构作答反应,以基于现实情境的统计开放题测验形式对小学生统计推理能力进行表现性评价.其中,测试题的编制主要以评价量规中的“3个评价指标”为理论指导.单题评分标准的编制以“4个评价等级”为理论指导,等级1“前结构水平”、等级2“单一结构水平”、等级3“多元结构水平”、等级4“关联水平”分别赋分为1分、2分、3分、4分,等级0(空白作答、无关作答)赋分为0分.同时,对每个等级下的学生作答进行双位编码,编码的第一位表示得分,第二位表示作答类型,如等级2中的编码“10”表示得“2分”中的“类型0”.由此,该套评价体系较好地实现了评价框架、测试题、评分标准的有机统一.

表1 小学生统计推理能力的评价量规
2.2.2 统计推理能力测试卷
基于研究构建的小学生统计推理能力评价量规,“统计推理能力测试卷”包含推测数据之外信息、运用数据解释推测、反思推测不确定性3个指标,每个指标含4道题,共12道题(1道画图题、2道简答题、1道填空题和8道解答题).该测试工具综合参考了国内外大规模测评、中小学统计教育研究和小学数学教材中的相关统计题,兼顾画图题、简答题、填空题、解答题等多种题型的分布,所选取的情境是学生熟悉的且可理解的、有吸引力、公平的但又不至于成为“强干扰”的现实情境.工具的研发先后经历了出声思维及访谈、第一轮小规模预测试、专家外审、第二轮大规模预测试等环节来保证试题质量.测试卷的内部一致性系数为0.76,符合测量学的基本要求[21].验证性因素分析结果为:2/=1.89,=0.053<0.06,=0.048<0.05,=0.93,=0.91,说明该测试工具的结构效度良好[22].
研究综合考虑课标要求、情境设计、素材呈现、文字表述、设问设计、干扰因素等方面来进行科学命题.图1呈现了测试题中的一道大题.该题的情境为跑步比赛,题型均为解答题.第(1)小题对应指标2“运用数据解释推测”,主要考查学生挖掘已有数据寻找尽可能多的证据的意识;第(2)小题对应指标3“反思推测不确定性”,主要考查学生对结论不确定性的反思.该题用统计表的形式呈现数据,是对原始数据的简单分类统计,涉及的知识点主要包括统计表(能读取统计表信息)和平均数(能用平均数比较甲乙运动员的比赛成绩).
2.3 研究过程
为有效获得学生表现数据,研究以班级为单位进行团体施测,由该班数学教师或班主任进行监考,研究者进行巡考.测试时长共60分钟.在测试结束后,由研究者完成所有试卷批阅工作.研究通过评分者内部一致性和评分者间的一致性两方面确保阅卷的信度.在评分者内部一致性方面,研究者在阅卷过程中,每完成100份试卷评阅者会从中随机抽取5%的试卷进行复审.在评分者间一致性方面,当阅卷结束后,研究者随机抽取20%已阅试卷,由3位数学教育领域研究生作为阅卷员对主观题进行双独立评分.每位阅卷员均需经过半小时的阅卷培训,由研究者向其说明阅卷目的、评分规则和注意事项.阅卷培训结束后,每位阅卷员将先试评5份试卷,直至评分结果达成一致.阅卷员通过试评后,3位阅卷员对20%的试卷进行核验,核验结果显示每道主观题与研究者的评分一致性均大于90%.
在数据整理和分析环节,采用Excel2019、SPSS22.0、Mplus8.0软件录入、清理和分析数据.其中,运用描述性统计、Rasch分析法对学生统计推理能力的总体表现进行分析,运用案例分析法将每个评价指标上的不同水平学生的典型表现案例进行分析.
3 研究方法
3.1 统计推理能力的总体表现
总体来看,六年级学生统计推理能力测验的总体得分率为54%.基于Rasch模型,运用期望后验估计法估计统计推理总分能力值和3个指标上的分维度能力值.学生的统计推理总分能力值的频数分布如图2所示.
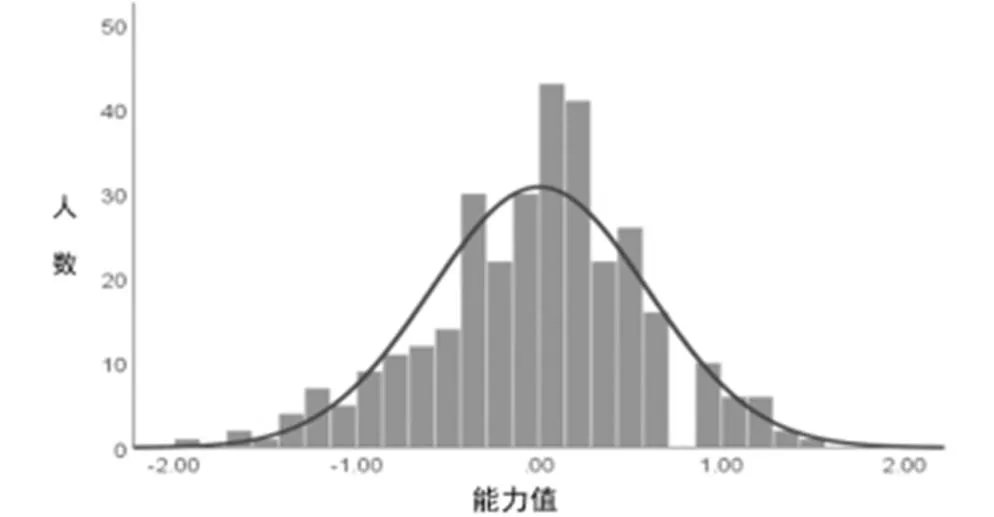
图2 六年级学生统计推理测验的总分能力值分布图
从学生在各指标上的能力值差异上看(见图3),六年级学生在推测数据之外信息上的能力值离散程度最大,说明学生在该指标上的能力值差异较大,两级分化严重.相比之下,六年级学生在反思推测不确定性上的能力值差异明显最小且得分更为集中.六年级学生在统计推理3个指标上的能力值平均水平大体相当,但学生在推测数据之外信息上的平均水平略高于其它两个指标.
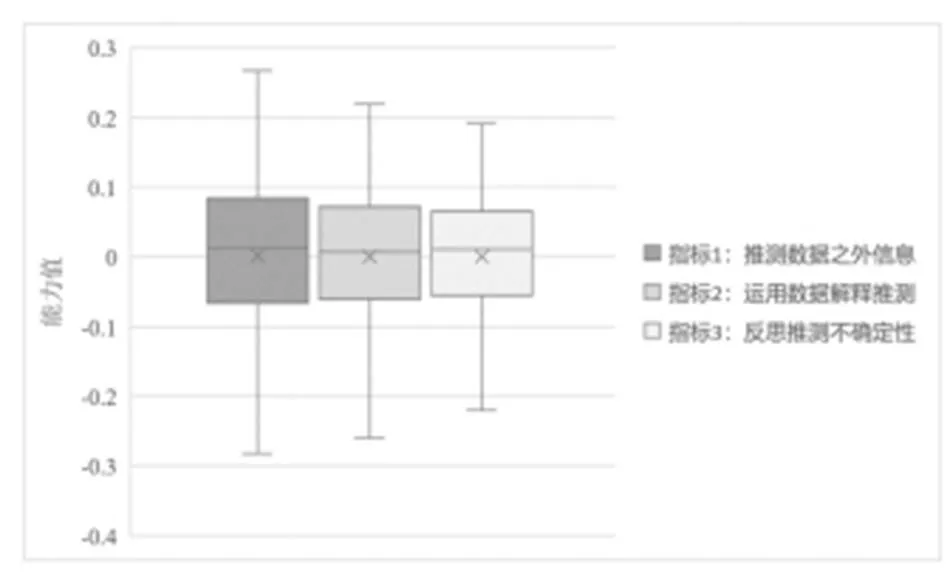
图3 六年级学生统计推理测验的各指标能力值分布
六年级学生在统计推理3个指标上的各等级人数分布有所差异(见表2).在指标1“推测数据之外信息”上,仍有14.0%的学生处于前结构水平,和其它两个指标相差较大.在指标2“运用数据解释推测”上,有36.4%的学生达到多元结构水平,明显比其它两个指标的该水平人数占比要多.对于指标3“反思推测不确定性”而言,有61.1%的学生处于单一结构水平,同指标2在该水平上的人数百分比相差了8.5%.

表2 六年级学生在统计推理能力各指标上的等级分布
注:“( )”内表示该指标对应水平的人数.
3.2 统计推理能力的表现案例
3.2.1 “推测数据之外信息”上的学生表现案例
学生推测数据之外信息的关键是把握数据的规律性和随机性,从而进行统计预测或推断总体.下面以学生在一道典型题上的4水平表现为例,分析学生的典型表现.

【典型题1】六(2)班共40人,他们开展了“身高调查”的统计活动.笑笑所在小组已经任意调查了全班20位同学,并整理了这20位同学的身高分布情况,如下图.图中每个黑圈“”代表已调查的1位同学.(1)请推测该班剩下20位同学的身高情况,用“○”表示,并将“○”继续添加在图中黑圈的上方.
六年级学生在“推测数据之外信息”时,处于前结构水平的学生基本忽视已有数据的规律,意识不到数据的随机性,他们所得推测基本是个人主观想法或极端判断.在典型题1中,有24.6%的学生处于前结构水平,这部分学生基本忽视已有数据规律,往往联系班内同学身高情况,按主观想法画该班剩下20位同学的身高分布.
处于单一结构水平的学生仅能把握数据的“规律性”或“随机性”其中之一,做推测时的思维简单且直接.有40.8%的学生处于单一结构水平,其中28.0%的学生能意识到已调查的20位同学是“任意选取的”,能够体会到20人之外的20位同学的身高数据和已调查的不一样,但他们难以恰当理解已有数据所蕴含的信息.例如,有的学生在推测剩下20人身高时,会将数据过度集中在150、151、152这几个数值上(见图4),可见这部分学生能够体会数据的随机性,但把握不好数据的规律性.此外,有9.9%的学生直接复制或基本复制已有的20人身高分布,这部分学生能够体会出数据的规律性,但缺乏随机意识.
处于“多元结构水平”的学生则大致能把握和兼顾数据“规律性”和“随机性”,但会忽视小部分因素.在该题中,有26.8%的学生处于多元结构水平,并有19.0%的学生能够按照已有数据规律来画并体现了数据的随机性,他们能在153~156处增加数据,但往往存在一些小缺陷.如图4(3)的学生案例所示,尽管该学生意识到这20人和已调查20人的身高分布会不相同,且整体分布符合已有数据规律,但他在149 cm、150 cm、152 cm处均画了3个圆,一定程度上忽视了已有数据在这3个身高点上所蕴含的数据规律.
处于“关联水平”的学生能较好地把握和协调数据的“规律性”和“随机性”,能全面地推测数据之外信息.在该题中,仅3.1%的学生处于关联水平.和“多元结构水平”的学生相比,这部分学生思考问题更加全面,能够聚焦整体让数据分布更加完整,会尽可能考虑到一些“小缺陷”.他们意识到,剩下20人的身高可能会分布在153 cm~156 cm之间,并且也能体会到已有数据的规律,即身高数据集中在150 cm~152 cm之间,且151 cm最多(见图4).
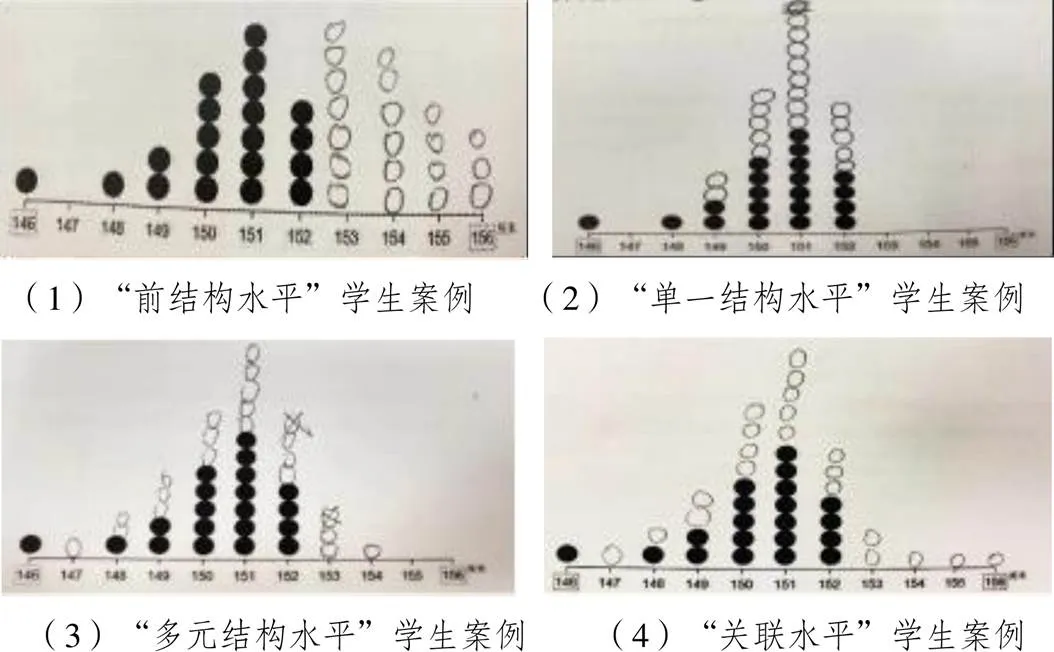
图4 典型题1的4水平学生表现
3.2.2 “运用数据解释推测”上的学生表现案例
学生运用数据解释推测的核心在于“自圆其说”,关键是用数据作为证据来“说话”,能从数据的多个角度或运用统计量(如平均数)来解释推测.下面将以学生在图1第(1)小题(典型题2)上的表现为例,分析学生在该指标上的典型表现.
处于前结构水平的学生基本不具有数据作为证据的意识,他们通常运用个人喜好、个人经验或仅基于情境来解释推测.如在典型题2中,有7.2%的学生处于前结构水平.这一水平的学生往往分成两类:一类是不具备数据作为证据的意识,运用个人喜好、个人经验或仅基于情境来解释推测,如作答“甲和教练关系更好”“甲爆发力强所以跑得快”等;另一类是具有数据作为证据的潜在意识,但毫无逻辑或表述非常不清楚.
处于单一结构水平的学生具有数据作为证据的初步意识,能基于对数据的直观感受,从数据的单一角度来简单解释推测.在该题中,有54.8%的学生处于单一结构水平,这部分学生已然能够运用数据作为证据来解释推测,但只能给出1个量化表征以外的理由.他们解释推测的策略主要包含4种(见表3).①纵向比较成绩发展趋势,如甲发挥得越来越好、甲跑得更稳定等.这一类学生占40.5%,是单一结构水平学生的典型作答.和多元结构水平的学生相比,这一部分学生只能相对直接地描述甲或乙从第1场到第5场的比赛成绩的高低变化,但不能进一步说明变化范围.②横向比较获胜次数,即指出甲的获胜次数比乙更高.③最值角度,即用甲乙最慢或最快的成绩进行说理.④就近思想,即用最近一次比赛(第5场)数据进行说理.

表3 “运用数据解释推测”典型题学生主要作答策略
处于多元结构水平的学生具有数据作为证据的基本意识,大多能从数据的多个角度或统计量的其中一类来解释推测.该题有31.2%的学生处于多元结构水平,作答策略主要有3种.①19.6%的学生能说出2个量化表征以外的理由,即对单一结构水平中的4种作答策略进行两两组合,如甲的获胜次数多且甲发挥得越来越好.②3.7%的学生能从整体视角出发,运用平均数、成绩总数、胜率等量化表征形式来说明数据的整体特征和集中趋势.③7.8%的学生给出的2个理由中有1个量化表征形式(见图5),这部分学生相比使用第一种策略的学生具有更好的定量分析意识.

图5 典型题2的多元结构水平和关联水平学生表现案例
处于关联水平学生具有数据作为证据的较强意识,相比多元结构水平学生解释推测时更加全面、完整和有逻辑性.该题仅有5.6%的学生处于关联水平,这部分学生能深度挖掘和综合数据所蕴涵的信息,能给出3个及以上的理由,如“获胜次数+最近场次+成绩发展趋势”“获胜次数+成绩发展趋势+平均数比较”等3种及以上数据解读视角相结合的说理策略(见图5).
3.2.3 “反思推测不确定性”上的学生表现案例
学生反思推测不确定性的关键在于知道要提高推测可靠性以及如何提高,本质上是对统计推理所得结论的反思和精进.下面将以学生在典型题3上的表现为例,分析学生在该指标上的典型表现.
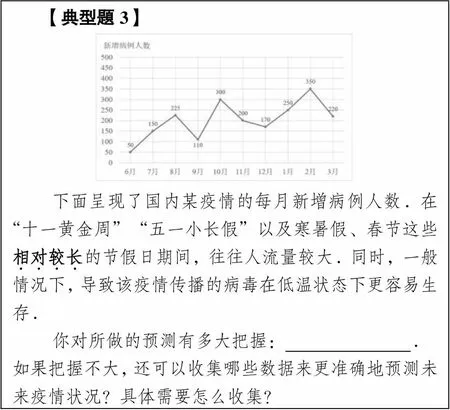
【典型题3】下面呈现了国内某疫情的每月新增病例人数.在“十一黄金周”“五一小长假”以及寒暑假、春节这些相对较长的节假日期间,往往人流量较大.同时,一般情况下,导致该疫情传播的病毒在低温状态下更容易生存.你对所做的预测有多大把握: .如果把握不大,还可以收集哪些数据来更准确地预测未来疫情状况?具体需要怎么收集?
六年级学生在“反思推测不确定性”时,处于前结构水平的学生对推测不确定性的判断是一种主观臆断,或极端地认为基于已有信息的推测毫无可靠性.典型题3中,有1.9%的学生处于前结构水平,这部分学生往往不能判断所得预测的不确定性,给出的收集数据建议是围绕“疫情”情境和已有题干信息的“擦边球式”作答,如建议收集人流量数据等.
单一结构水平的学生往往囿于手头上数据难以跳脱出来,即便他们能意识到要提高推测可靠性,也不知道如何提高,提出的改进策略往往同统计情境搭边但无效.该题有70.4%的学生处于单一结构水平,其中有29.6%的学生表示了对自己所得预测的不确定性,但他们给出的数据收集建议和前结构水平学生雷同,是围绕“疫情”情境的“擦边球式”作答.也有24.6%的学生表示了预测的不确定性,但给不出数据收集建议或建议错误(见图6).此外,也有15.0%的学生对所得预测完全确定、相当确定,且所给建议错误或部分完整.
处于多元结构水平的学生能清楚地意识到推测是不确定的,大多知道收集哪些数据来提高推测可靠性并尝试说出改进策略,但往往不知道怎样收集这些数据,也难以详细说明具体该如何做.在该题中,有18.4%的学生处于多元结构水平,这部分学生的表现可根据所表达的不确定性语言类型大致分为两种.①9.3%的学生能用定性语言表示所得预测的不确定性,且给出的数据收集建议部分合理,他们往往能说明收集什么数据来提高疫情预测的可靠性,如收集疫苗接种数据、收集历年数据等(见图6).②8.4%学生能用定量语言(如70%)表示所得预测的不确定性,且给出的数据收集建议部分合理(见图6).
关联水平的学生对如何提高推测可靠性的认识是深刻、彻底的,他们能够完整、详细地说明收集什么数据和怎样收集数据.在该题中,共有4.7%的学生处于关联水平,这部分学生能详细地说出收集什么数据和怎样收集数据.如:收集前几年的数据或国外疫情数据,可以从国家数据库或新闻网站上搜索.同样,这一水平学生的表现也可分为使用定性语言(人数占比1.9%)或用定量语言(人数占比2.8%)表达预测不确定性这两种(见图6).这一水平学生往往能跳脱已有题目情境本身,对和该情境相关的数据进行关联,由此为该情境下推测可靠性的提高提供进一步的证据.

图6 典型题3的不同水平学生表现案例
4 结论与讨论
(1)总体上,大多数六年级学生的统计推理能力处于单一结构水平和多元结构水平,少数学生仍处于前结构水平,极少数能达关联水平.
研究通过对B市郊区321名六年级学生的统计推理测验发现,有86.0%~90.4%的六年级学生在统计推理3个指标上处于单一结构水平和多元结构水平.其中,52.6%~61.1%的学生处于单一结构水平,28.7%~36.4%的学生处于多元结构水平.这一结果说明,超过五成的六年级学生的统计推理能力处于单一结构水平,近九成六年级学生的统计推理能力已然处于单一结构水平和多元结构水平.相比而言,仅有少数学生的统计推理能力仍处于前结构水平这一较低层次,且极少数学生能达关联水平.该结果可得到已有相关研究的支持,如Callingham和Watson的大规模实证研究结果显示,澳大利亚六年级学生的统计素养和推理水平大多处于单一结构水平,并逐步向多元结构水平过渡,而在关联水平和前结构水平的比例则相对较低[23].
六年级学生的统计推理能力水平和该年龄段学生的认知发展特点息息相关.根据皮亚杰的认知发展理论,六年级11~12岁的学生正处于具体运算阶段向形式运算的过渡阶段,这一阶段的学生考试逐渐离开具体事物,根据假设来进行逻辑推演[24].SOLO分类理论中的关联水平可对应皮亚杰认知发展理论中的形式运算阶段[25].这个年龄段的学生能从一个角度或多个角度出发较好地处理问题,但对抽象思维、逻辑思维有更高要求的题目,他们的思维发展水平尚难达到.这也进一步解释了为何只有少数六年级学生可达关联水平,而大多学生还是处于单一结构和多元结构水平.
(2)在“推测数据之外信息”上,仍有一定比例学生受困于基于主观经验做出推测而处于前结构水平;单一结构水平学生的表现特征和已有研究有所出入,部分学生所做推测能体现出不确定性,但会偏离数据规律.
对数据之外信息的推测在中国小学数学课程标准和课程体系相对被弱化.尽管如此,研究发现,已然有57.3%的学生可以到达单一结构水平,28.7%的学生达到较高层次的多元结构水平.受限于相应学习机会的缺乏,低层次的前结构水平学生得不到相应的教学支持而陷于困境.结果显示,在“推测数据之外信息”指标上,仍有14.0%的六年级学生处于前结构水平,这一比例和其它两个指标相差了4.7%~8.1%.结合前结构水平学生在“推测数据之外信息”上的表现特征可发现,这部分学生的关键表现特征为基于个人主观经验或统计情境做出推测,容易被无关信息所干扰.尤其是面对自己过于熟悉的统计情境时,他们很容易持有一种“先入为主”的偏见或误解[26],这种偏见或误解会成为该水平学生思考时的“强干扰”,从而抹灭他们做出推测过程.
具体而言,在“推测数据之外信息”指标上,前结构水平、多元结构水平、关联水平学生的表现特征可得到相关研究的支持[14,17].然而,研究所得的单一结构水平的学生表现特征同部分研究结果有所差异.如Goss的实证研究发现,单一结构水平的学生很少能体会到数据随机性,且得到的是确定性结论[19].但研究结果显示,单一结构水平学生做出的推测除了表现为确定性结论,还有相当一部分学生所做推测是不确定的、随机的.他们的推测同时也会偏离已有数据所蕴涵的信息和规律.他们可能因为受限于生活经验和学习经验,所以往往意识不到不确定性背后会有规律可循.
(3)绝大部分六年级学生能运用数据解释推测,且相对其它两个指标,在该指标处于多元结构水平和关联水平的学生最多;各水平学生的表现特征同已有研究基本一致,但在运用“怎样的数据”解释推测上存在差异.
研究结果显示,90.1%的学生在“运用数据解释推测”上处于单一结构及以上水平,已然具备运用数据作为证据的初步意识.有37.3%的学生处于多元结构水平和关联水平,能从数据的多个角度或运用统计量来解释自己的推论和预测.在统计推理的3个指标中,“运用数据解释推测”指标上处于高水平的学生最多,绝大部分六年级学生能运用数据解释推测,这一结论可得到许多研究的支持.如Gil和Ben-Zvi针对以色列六年级学生的实证研究发现,很大一部分六年级学生能用数据进行不同程度的说理或解释[27].张丹针对中国六年级学生的研究发现,大部分学生已经能基于给出的数据进行合理推断,并开始从数据整体来解释和说理,观察数据的角度也更加完整[4].
具体而言,在“运用数据解释推测”指标上,研究发现4个水平学生的表现特征同已有研究结果基本一致[17].相比国际上的相关研究,研究还发现了六年级学生在运用“怎样的数据”解释推测时的一些特点.例如,English和Watson针对澳大利亚六年级学生的实证研究发现,在基于已有比赛成绩选拔运动员时,学生更喜欢运用“最佳成绩”和“平均数”来说理[28].在同样的题目情境和相似设问下,研究以中国六年级学生为研究对象,发现他们更喜欢运用“成绩发展趋势”来说理,但缺乏自发地运用平均数进行说理的意识.尽管中国学生在小学阶段已多次接触和正式学习了平均数,但真正能在题目没有明确要求和暗示下自觉运用平均数“说话”的学生却是少数.
(4)在“反思推测不确定性”上,学生能用不确定性语言进行表达并不代表他们能真正意义上反思推测的不确定性,且有较多比例的学生受困于“确定性思维定势”和对已有数据“缺陷”的认识不足而处于单一结构水平.
研究结果显示,有61.1%的学生在“反思推测不确定性”指标上处于单一结构水平.同“推测数据之外信息”指标上的表现特征类似,六年级学生在“反思推测不确定性”时,较多处于单一结构水平的学生能意识到所做推测是不确定的.这一结果同已有研究有所出入.如Henriques和Oliveira针对葡萄牙八年级学生的实证研究发现,很少有学生能使用不确定性语言来表达推测不确定性[29].但进一步挖掘单一结构水平学生的思维特征可发现,即便这部分学生能用不确定性语言进行表达,也不代表他们能真正意义上反思推测的不确定性,而其根本原因主要有二.一是他们在做统计推理时受困于“确定性思维”.即便有学生尝试提出策略,也往往是和已有数据搭边但无效的策略,依旧难以跳脱已有数据本身去提出提高推测可靠性的策略.在中国小学阶段的数学学习过程中,“数与代数”“图形与几何”领域的内容占了很大篇幅,小学生在数学学习中往往是追求一个确定的、固定的答案,这样的确定性思维在学生心中已然是“根深蒂固”.而统计推理本身是研究“不确定性”的学问,这需要学生打破“确定性”的思维定式,这无疑对小学生而言是有挑战的.二是他们对已有数据“缺陷”的反思不足,本质上是忽视了一定统计情境和统计目的背景下数据收集的需求和必要性.数据作为“情境中的数”[30],最终也应回到数据情境和统计问题之下去思考——为何这样收集数据以及为何收集这些数据?
相比之下,研究发现处于多元结构水平和关联水平的学生(占比32.1%)已然能跳脱已有数据本身,用不确定性语言表达推测不确定性,并真正认识到所做推测是不确定的.多元结构水平的学生还能说出收集什么数据,关联水平的学生还能在此基础上具体说出怎样收集数据.这两个水平学生能真正联系统计情境和统计目的来思考数据的缺陷和反思所做推测的可靠性,并从不同程度上提出提高推测可靠性的有效策略.
[1] BAKKER A, KENT P, DERRY J, et al. Statistical inference at work: Statistical process control as an example [J]. Statistics Education Research Journal, 2008, 7 (2): 130-145.
[2] OECD. PISA2021 mathematics framework (draft) [M]. Paris: OECD, 2018: 15.
[3] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022:6.
[4] 张丹.小学生如何学习数据分析——基于学习过程的实证研究[M].上海:上海教育出版社,2020:148-166.
[5] 董瑶瑶,刘坚.小学数学教师的统计推理信念研究[J].中小学教师培训,2022(4):50-54.
[6] VISNOVSKA J, COBB P. Supporting shifts in teachers’ views of a classroom statistical activity: Problem context in teaching statistics [J]. Mathematical Thinking and Learning, 2019, 21 (4): 285-305.
[7] 李化侠.学习进阶视角下小学生统计思维发展水平研究[J].数学教育学报,2019,28(6):55-60.
[8] 董瑶瑶,杜宵丰,刘坚.基于SOLO分类理论的小学统计开放题评价研究——以D市大规模测试为例[J].数学教育学报,2022,31(6):11-16.
[9] 高翔.澳大利亚RMFII项目中“统计推理”的引介与思考[J].数学教育学报,2022,31(4):62-67.
[10] GARFIELD J. The challenge of developing statistical reasoning [J]. Journal of Statistics Education, 2002, 10 (3): 1-12.
[11] 石文静.高中生统计推理思维结构的研究[D].北京:北京师范大学,2008:2-4.
[12] ZIEFFLER A, GARFIELD J, DELMAS R, et al. A framework to support research on informal inferential reasoning [J]. Statistics Education Research Journal, 2008, 7 (2): 40-58.
[13] MAKAR K, RUBIN A. A framework for thinking about informal statistical inference [J]. Statistics Education Research Journal, 2009, 8 (1): 82-105.
[14] DE VETTEN A, SCHOONENBOOM J, KEIJZER R, et al. Pre-service primary school teachers’ knowledge of informal statistical inference [J]. Journal of Mathematics Teacher Education, 2019, 3 (22): 639-661.
[15] 李星云.论小学数学核心素养的构建——基于PISA2012的视角[J].课程·教材·教法,2016,36(5):72-78.
[16] WATSON J M, MORITZ J B. The longitudinal development of understanding of average [J]. Mathematical Thinking and Learning, 2000, 2 (1): 9-48.
[17] JONES G A, THORNTON C A, LANGRALL C W, et al. A framework for characterizing children’s statistical thinking [J]. Mathematical Thinking and Learning, 2000, 2 (4): 269-307.
[18] 潘禹辰,李亚琼,徐文彬,等.国际统计教育研究的议题和趋势及其启示——《国际统计教育研究手册》评述[J].数学教育学报,2022,31(5):82-89.
[19] GOSS J M. A method for assessing and describing the informal inferential reasoning of middle school students [D]. Kalamazoo: Western Michigan University, 2014: 50.
[20] SRI PADMI I. Developing 7th grade students’ informal inferential reasoning [D]. Surabaya: Surabaya State University, 2015: 10.
[21] CORTINA J M. What is coefficient alpha? An examination of theory and applications [J]. Applied Psychology, 1993, 78 (1): 98-104.
[22] 温忠麟,侯杰泰,马什赫伯特.结构方程模型检验:拟合指数与卡方准则[J].心理学报,2004,36(2):186-194.
[23] CALLINGHAM R, WATSON J. The development of statistical literacy at school [J]. Statistics Education Research Journal, 2017, 16 (1): 181-201.
[24] 皮亚杰.皮亚杰教育论著选[M].卢濬,译.北京:人民教育出版社,1990:20-35.
[25] 蔡永红.SOLO分类理论及其在教学中的应用[J].教师教育研究,2006,18(1):34-40.
[26] FRISCHEMEIER D, SCHNELL S. Statistical investigations in primary school: The role of contextual expectations for data analysis [J]. Mathematics Education Research Journal, 2023, 35 (1): 217-242.
[27] GIL E, BEN-ZVI D. Explanations and context in the emergence of students’ informal inferential reasoning [J]. Mathematical Thinking and Learning, 2012, 13 (1): 87-108.
[28] ENGLISH L D, WATSON J M. Modelling with authentic data in sixth grade [J]. ZDM, 2018, 50 (7): 103-115.
[29] HENRIQUES A C, OLIVEIRA H. Students’ expressions of uncertainty in making informal inference when engaged in a statistical investigation using tinkerplots [J]. Statistics Education Research Journal, 2016, 15 (2): 62-80.
[30] COBB G W, MOORE D. Mathematics, statistics, and teaching [J]. American Mathematical Monthly, 1997, 104 (9): 801-823.
An Empirical Study of Primary School Students’ Statistical Reasoning Performance
DONG Yao-yao1, 2, LIU Jian1, 2
(1. Collaborative Innovation Center of Assessment toward Basic Education Quality, Beijing Normal University, Beijing 100875, China;2. China Education Innovation Institute, Beijing Normal University, Guangdong Zhuhai 519087, China)
The development of primary school students’ statistical reasoning ability helps to promote students to develop a rational spirit of “speaking with data”, which is in line with the literacy requirements of modern citizens in the era of big data. In this regard, a mixed research method is adopted. Taking 322 sixth-grade students from an ordinary public primary school as the research participants, the performance assessment is carried out based on the rubric of statistical reasoning ability. The current study depicts the overall performance and typical performance characteristics of students’ statistical reasoning. The results show that: in terms of overall performance, nearly 90% of the sixth-grade students’ statistical reasoning is at the Uni-structural level and Multi-structure level, and more than 50% of the students are at the Uni-structural level; a few students are still at the Pre-structure level, and very few can reach the Relational level. In terms of specific performance characteristics: 86.0 % of sixth graders can infer information beyond the data; 90.1% of sixth graders can use data as evidence to preliminarily explain the inference; 32.1% of them could really reflect on the uncertainty of the inference; and on the three indicators, students have different answering strategies and learning myths. As a result, by realizing the organic unity of the assessment framework, test items, and scoring standards, an assessment system for statistical reasoning ability is constructed, which reveals the reasoning cognitive process in the “statistics” area. The application provides a foundation for promoting the development of students’ statistical reasoning ability and the cultivation of data awareness and reasoning awareness.
primary school; statistical reasoning; rubric; assessment; SOLO; data awareness; reasoning awareness
G625.5
A
1004–9894(2024)01–0036–08
董瑶瑶,刘坚.小学生统计推理能力表现的实证研究[J].数学教育学报,2024,33(1):36-43.
2023–09–25
教育部教育管理与改革专项课题研究项目——德体美劳教育过程性评价框架研究(21JGWT0027);北京师范大学中国基础教育质量监测协同创新中心——区域教育质量健康体检项目(110105006)
董瑶瑶(1996—),女,浙江宁波人,博士生,主要从事数学教育、教育评价研究.刘坚为本文通讯作者.
[责任编校:张楠、陈汉君]

