基于区间随机阶矩的不确定量化方法
邱继伟,罗海胜,赵冠捷,张 亚
(中国兵器工业标准化研究所,北京 100089)
0 引言
齿轮—转子系统是兵器、船舶、航空、航天等领域中应用最广泛的动力传递装置。随着对齿轮—转子系统的传动精度、承载能力、可靠性、低噪声等的要求越来越高,有关齿轮—转子系统振动问题的研究也越来越重要[1-2]。目前齿轮—转子系统动力学研究大多处理为确定性问题[3-5],轴系扭转振动模型完全可以比较精确地对确定性分析问题进行建模和仿真,然而实际工程中由于制造、装配、润滑、冲击、温度等因素都会导致齿轮—转子系统参数存在不确定性,而含有不确定性参数的扭振模型无论解析法还是数值方法都很难直接进行运算,无法定量描述系统响应的边界。当前齿轮—转子系统的动态特性不确定分析主要采用基于统计模型的分析方法[6-8],该方法可以处理含随机变量的不确定性问题,而不确定性不等同于随机性,统计分析方法并非研究齿轮—转子系统不确定问题的唯一方法。另外,统计分析方法往往需要大量样本实验来获取已知系统参数或激励的统计信息,然而由于自然现象的复杂性和人们认知的局限性,有些参数很难获得甚至无法获得。相比统计信息,研究人员可以根据所掌握的知识和工程经验积累情况相对容易地给出一些不确定参数的上下边界信息,即区间信息,进而使齿轮—转子系统振动分析中同时包含随机信息和区间信息,因此研究同时含随机参数和区间参数的齿轮—转子系统的动力分析问题具有重要的理论意义和工程背景。
国内外学者对随机不确定性传播和区间不确定性传播问题进行了大量研究。研究随机不确定性传播的手段主要是混沌多项式展开、傅里叶级数展开等。PANUNZIO等[9]将混沌多项式和渐近数值方法结合,提出非入侵式振动传播方法,并计算了机构系统随机共振频率、峰值振幅;DUBREUIL等[10]针对随机系统多学科分析问题,提出基于多项式混沌扩展的半侵入混沌多项式分析方法,有效地将这些随机不确定性传播到多学科分析的输出解中;VIVEK VITTALDEV等[11]结合高斯混合模型与多项式混沌展开方法,提出基于高斯混合模型和多项式混沌展开的航天器不确定性传播方法;余学锋等[12]针对基于国际标准化组织ISO《测量不确定度指南》提供的测量不确定度评估方法存在的局限性,提出采用多项式混沌方法进行测量结果不确定度评估的新方法。研究区间不确定性传播问题的手段主要是Chebyshev多项式、泰勒级数多项式、区间扩张函数等。WU[13]等将切比雪夫级数展开引入区间模型,提出一种新的区间不确定系统的动态响应分析方法,有效提高了数值解的精度;FEDELE等[14]提出一种新的基于区间逆问题的不确定性传播方法,基于迭代思想,利用区间有限元和优化技术直接估计未知参数的边界;TRABELSI等[15]用区间表示设计变量,在仿真步骤前集成所有不同类型的约束,以生成的时间间隔代表产品设计变量可能值的域,进而提出一种新的区间估计和约束传播算法;尹盛文等[16]针对修正一阶区间摄动有限元法存在的一阶泰勒展开误差较大和求解摄动逆矩阵时计算效率不高的缺陷,提出区间矩阵分解摄动有限元法。然而实际问题中,随机和区间不确定性变量往往共存,上述单一模型均不适用。
目前已有少量文献研究随机和区间不确定性变量共存的系统动态特性不确定性分析问题。ZAMAN等[17]针对系统分析中的不确定性表征和传播问题,提出一种区间和随机变量不确定的概率框架,该方法将区间变量进行Johnson分布拟合,在概率框架下计算了系统响应累积分布函数的严格界限;XIA等[18]针对缺乏充分信息来构造不确定参数精确概率分布的结构声学系统,提出一种混合不确定参数结构声学系统的区间随机摄动法,在区间随机模型的基础上,建立了区间随机结构声学有限元方程,提出区间随机摄动法求解该区间随机方程,然而该方法只适用于单调性函数;SHAH等[19]在偶然不确定性和认知不确定性共存的情况下,基于D-S证据理论,应用裕度与不确定性量化方法对复杂工程系统的性能和可靠性进行了评估,提出基于证据理论和随机多项式展开的裕度不确定性量化方法;WANG等[20]针对含模糊和区间参数的结构—声学耦合系统的混合不确定性传播问题,基于有限元框架和不确定性分析理论,提出一阶子区间摄动有限元法和改进子区间摄动有限元法,该方法对求解具有混合不确定参数的工程结构声学问题具有较高的精度和有效性;孙东阳等[21]针对机械系统中的混合不确定性量化问题,提出随机和认知不确定性量化的置信区域法,该方法分别用概率论方法和区间方法处理混合不确定性中的随机不确定性和认知不确定性,得到混合不确定性的置信区域,并以质量—弹簧—阻尼系统为例讨论了基于混合不确定性分析方法的有效性。上述研究方法大都局限于数值分析或时域频域仿真分析,数值解方法求解动力学方程时涉及较复杂的计算迭代过程,效率低且每次迭代的舍入误差大大影响了分析精度,仿真分析方法能确定趋势,但不能定量描述系统响应的波动规律。
综上所述,针对随机—区间参数共存的齿轮—转子系统固有特性不确定性分析问题,本文提出基于区间随机阶矩技术的不确定性量化方法。首先,表征了齿轮—转子系统固有频率的近似解;然后,研究了基于区间随机阶矩技术的不确定性量化方法,推导了齿轮—转子系统固有频率含随机—区间参数的均值和标准差表达式,并通过上下界相对不确定量与曲线凹凸性分析了区间参数影响系统响应和固有频率的规律;最后,应用齿轮—转子机构系统数值案例验证了本文方法的正确性和有效性。
1 齿轮—转子机构系统固有频率近似解表征
1.1 齿轮—转子扭振模型[22-23]
图1所示为单对齿轮转子系统示意图,该齿轮转子系统中的输入原动机(电机等)、主动齿轮、被动齿轮和输出负载(执行机构等)均等效为圆柱体,进而等效为4个转动惯量元件,其中主动齿轮和被动齿轮等效为相同厚度的圆柱体,因此该齿轮转子系统可简化为4自由度纯扭转振动系统。图1中Tm为原动机外力距,Tl为负载的外力距,Im为原动机等效转动惯量,Ip为主动齿轮等效转动惯量,Ig为被动齿轮等效转动惯量,Il为负载等效转动惯量,θm为原动机扭转角位移,θp为主动齿轮扭转角位移,θg为被动齿轮扭转角位移,θl为负载扭转角位移,cm为啮合阻尼,cp主动轴扭转阻尼,cg为被动轴扭转阻尼,km为啮合刚度,kp为主动轴扭转刚度,kg为被动轴扭转刚度。

考虑齿轮—转子系统为纯扭转工况,建立如下4自由度扭振分析模型:
(1)
(2)
(3)
(4)
式中:Wd为齿轮啮合刚度;Rp为主动齿轮基圆半径;Rg为被动齿轮基圆半径。
本文着重分析齿轮—转子系统的固有特性,因此建立自由振动方程
(5)
式中:M为质量矩阵;K为刚度矩阵;θ为扭转振动位移向量。
(6)
式中:ρ为材料密度;b为主被动齿轮齿面宽度;m为主被动齿轮模数;zp为主动齿轮齿数;zg为被动齿轮齿数;α为主动齿轮压力角。
(7)
式中:E为弹性模量;R1为主动连接轴半径;l1为主动连接轴长度;v为泊松比;R2为被动连接轴半径;l2为被动连接轴长度。
θ=[θmθpθgθl]Τ。
(8)
1.2 齿轮—转子系统固有频率近似解表征
在实际工程中,由于齿轮—转子系统的ρ,E,v,b,m,α,R1,R2,l1,l2等参数均有不确定性,导致与这些物理参数和几何参数相关的Im,Il,km也成为不确定性变量,因此齿轮—转子系统各阶固有频率也具有不确定性。
1.2.1 质量刚度矩阵不确定性表征
齿轮—转子系统的自由振动方程的特征方程表示为
|K-ω2M|=0。
(9)
式中ω为系统固有频率。
结合矩阵运算特征,将质量矩阵M和刚度矩阵K分解为若干个由确定性矩阵和不确定性参数集合相乘的子矩阵,并以矩阵和的形式进行表征,该分解能有效避免矩阵的不确定性运算,降低运算的复杂程度。
将质量矩阵M分解为
将刚度矩阵K分解为

(11)
1.2.2 齿轮—转子系统固有频率近似表征
引入Rayleigh quotient公式近似表征齿轮—转子系统固有频率,Rayleigh quotient公式[24]为
(12)
式中:ωi为齿轮—转子系统的第i阶固有频率;ui为在物理参数和几何参数均为确定变量下齿轮—转子系统的第i阶固有频率对应的特征向量。
结合式(10)~式(12),近似表征齿轮—转子系统含不确定性变量的固有频率为
(13)
2 区间随机阶矩量化方法
2.1 区间随机变量的定义
根据不确定性因素的产生机理可将不确定性分为随机不确定性和认知不确定性,本文的随机不确定性变量用随机模型表示,认知不确定性变量用区间模型表示(本文不考虑模糊不确定性问题)。随机不确定性是具有某一概率的事件集合中的各个事件所表现出来的偶然性,原因是条件不充分,使得条件和事件之间不能出现决定性的因果关系,导致在事件发生的结果上表现出不确定性;认知不确定指在认识客观事物的过程中,受知识水平、认知手段等因素的制约,现有信息不足以确定事物的真实状态而产生的主观认识上的不确定性。
材料物理参数(泊松比、弹性模量、材料密度等)、几何参数(结构外形参数、装配参数、截面参数等)的不确定性通常用随机不确定性模型表示,为随机变量。材料物理参数主要由于加工过程中存在“不均匀”现象(如有缺陷或裂纹等问题),这种“不均匀”的发展通常近似服从某一特定类型分布的随机过程,导致材料物理参数呈现不确定性;几何参数的不确定性是由于加工装备、制造工艺、装配工艺、测量工具及方法等不同,导致实际制造出的几何尺寸与设计要求的几何尺寸不可避免地存在误差,这些误差也近似服从某一特定类型分布的随机过程,亦可用随机不确定性模型表示。载荷的不确定性、初始条件和边界条件的不确定性等较多地呈现为认知不确定,可以用区间不确定性模型和模糊不确定性模型表示,通常为区间变量和模糊变量(本文不考虑模糊变量)。区间不确定性模型能够借助样本数据、实验数据、知识经验等明确参数变化范围,但不能确定概率密度函数的不确定参数。随机变量和区间变量定义如下:
(1)随机变量 概率空间(Ω,F,p)上的随机变量x是定义于Ω上的实值可测函数,即对任意ω∈Ω,X(ω)为实数,且对任意实数x,使X(ω)≤x的一切ω组成的Ω的子集{ω:X(ω)≤x}是事件,即是F中的元素。
(2)区间变量 区间通常指这样的一类实数集合:如果x和y是该实数集合中的两个数,则任何x和y之间的数也属于该集合。例如,由符合0≤x≤1的实数构成的集合便是一个区间,其包括0,1,以及0和1之间的全体实数。
本文不考虑变量之间的相关性,可将由随机变量Xi和区间变量Xj组成的区间随机向量X表示为
(14)

独立区间随机向量X的均值E(X)和方差var(X)表示为:
E(X)=(E(X1),…,E(Xi),…,E(Xn),E(Xn+1),
…,E(Xj),…,E(XN));
var(X)=(var(X1),…,var(Xi),…,var(Xn),
var(Xn+1),…,var(Xj),…,var(XN))。
(15)
将区间变量向量表示为随机变量向量的分布参数形式:
(16)

将区间变量表示为随机变量的分布参数形式:

(17)

通过式(16)和式(17)将区间变量表示为随机变量的分布参数形式,因此所有随机向量和区间向量构成一个新的随机区间向量
(18)
2.2 区间随机阶矩算法
2.2.1 多维区间随机函数泰勒展开
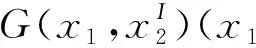

(19)
式中E(·)为随机变量(·)的均值。
式(19)给出了简单独立随机区间函数的一阶泰勒展开方法和具体表达形式,下面将该方法扩展到同时含有多维随变量和多维区间变量的函数中,同样各变量之间相互独立。假设某不确定机构系统响应函数为G(X(x,xI)),该响应函数中同时包括系统随机不确定性变量向量x和区间不确定性变量向量xI,则该系统响应函中的不确定性变量为2.1节中定义的独立区间随机不确定性变量。假设G(X(x,xI))是一个关于独立区间随机不确定性向量X(x,xI)的多维区间随机变量函数,即
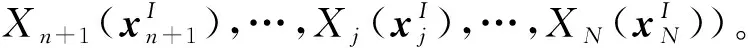
(20)
为了获得区间随机函数G(X(x,xI))的区间均值和标准差,本节基于泰勒展开公式提出区间随机阶矩算法。
根据泰勒展开公式,将区间随机函数G(X(x,xI))在区间随机向量的均值X(x,xI)处展开为
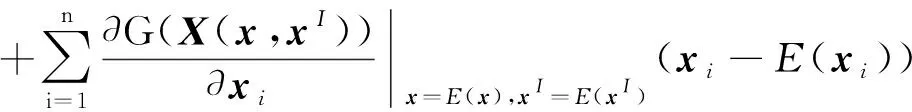
(21)
式中:x为随机不确定性变量向量;xI为区间不确定性变量向量。则区间随机变量向量X(x,xI)的均值E(X(x,xI))为一个区间随机不确定性变量向量。式(21)中的G(E(X(x,xI)))可以利用一阶泰勒级数在区间随机变量向量的均值处展开:

(22)

(23)
类似于G(E(X(x,xI))),式(21)中等号右侧第2项可以表示为
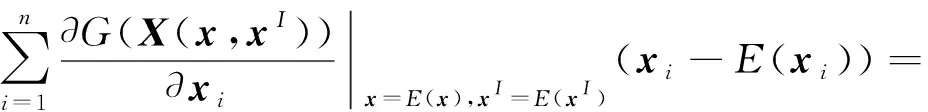
(24)

(25)
将式(23)~式(25)带入式(21),得:
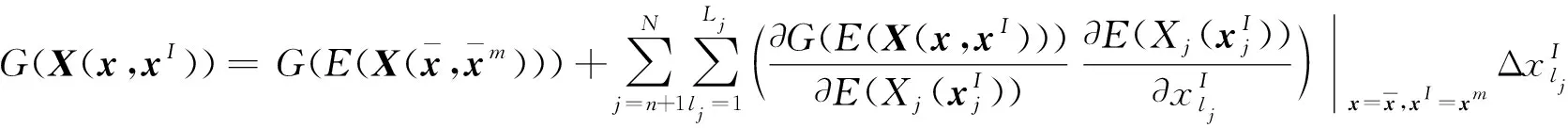
(26)
2.2.2 区间随机阶矩法
(1)随机变量函数阶矩法
对于随机变量,随机函数阶矩方法可以很容易地计算出函数的均值和方差[25-26]。现简单介绍随机函数阶矩法。
假设x=(x1,x2,…,xn)为随机不确定性变量向量,随机不确定性函数可表示为G(x)=G(x1,x2,…,xn),则随机不确定性函数G(x)的均值和方差表示为:
E(G(x))=G(E(x))=
G(E(x1),E(x2),…,E(xn));
(27)

(28)
式中:E(·),Var(·),σ(·)分别为随机变量(·)的均值、方差和标准差;cov(xi,xj)为随机变量xi和xj的协方差。式(28)还可以表示为

(29)
式中ρ(xi,xj)为随机变量xi和xj的相关系数。
因为本节考虑不确定性变量均为相互独立的,所以式(29)可改写为
(30)
(2)区间随机阶矩算法
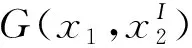
均值和方差如下:
(31)
(32)
由式(26)可得不确定性机构系统响应函数G(X(x,xI))(多维区间随机函数)的一阶泰勒展开形式,结合式(31)和式(32),推导多维区间随机函数的均值和标准差如下:

(33)
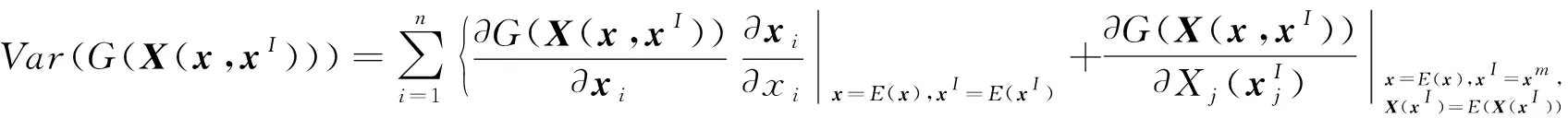
(34)
(3)区间运算法则
例如,对于实数x,y,z,t,区间运算的四则运算法则如下:
[x,y]+[z,t]=[x+z,y+t];
(35)
[x,y]-[z,t]=[x-t,y-z];
(36)
[x,y]×[z,t]=[x×z,y×t];
(37)
[x,y]/[z,t]=[x/t,y/z],z>0;
(38)
min([x,y],[z,t])
=[min(x,z),min(y,t)];
(39)
max([x,y],[z,t])
=[max(x,z),max(y,t)]。
(40)
需要注意的是,式(37)和式(38)所对应的区间乘法和区间除法,要比最原始的区间运算简单。对于在范围为(-∞,+∞)的实数,一般形式下的区间乘法和区间除法比较复杂,为
[x,y]·[z,t]=[min(x·z,x·t,y·z,y·t),
max(x·z,x·t,y·z,y·t)];
(41)
[x,y]/[z,t]=[min(x/z,x/t,y/z,y/t),
max(x/z,x/t,y/z,y/t)],z,t≠0。
(42)
基于实数四则运算法则和区间运算法则以及上述推导的均值和方差计算公式,便可获得响应函数均值和方差波动范围。
3 案例分析
3.1 齿轮—转子系统随机和区间变量
某一装备中的齿轮—转子系统可简化为如图1所示的单对齿轮副纯扭转振动模型,在输入原动机(电机等)、主动齿轮、被动齿轮和输出负载(执行机构等)均等效为圆柱体的基础上,研究齿轮—转子系统的4自由度纯扭转振动问题。相关建模及固有频率的近似解表征过程见第2章。该齿轮—转子系统中的随机不确定性变量取值如表1所示[23],区间不确定性变量取值范围如表2所示[22],主被动齿轮的齿数zp=19,zg=48为确定性变量,研究齿轮—转子机构系统固有频率的波动情况。

表1 随机变量均值及标准差

表2 区间变量取值范围
3.2 计算过程和结果
在随机变量取均值、区间变量取中值的确定性条件下,由式(9)计算齿轮—转子机构系统的四阶固有频率分别为0 Hz,266.8 Hz,524.3 Hz,3 362.2 Hz,可知二阶固有频率与负载激振频率比较接近,产生共振的可能性很大。由于机构系统内含有大量不确定性变量,固有频率可能会产生很大波动,是否产生高阶共振需要进一步量化各阶固有频率的波动范围。通过含不确定性参数的齿轮—转子系统固有频率显式推导方法和式(13)可以获得二阶、三阶和四阶固有频率显式表达。
根据2.2节基于区间随机阶矩技术的混合不确定性量化方法,获得齿轮—转子机构系统二阶、三阶和四阶固有频率均值及方差的上下界,如表3所示。
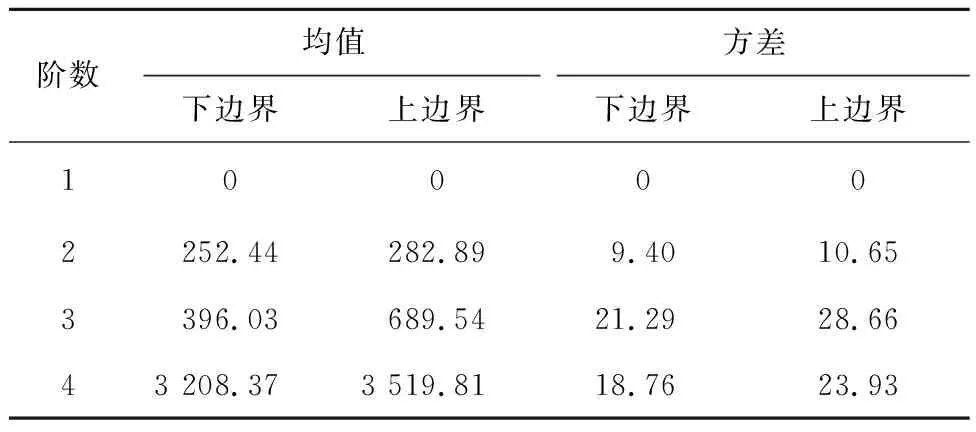
表3 齿轮—转子机构系统固有频率均值和方差上下边界 Hz
由表3可知,二阶固有频率均值的波动范围为[252.44,282.89],对应方差的波动范围为[9.40,10.65],而负载激振频率波动范围为[280,310],激振频率区间范围与二阶固有频率波动范围有交叉,三阶和四阶固有频率波动范围与激振频率区间范围不存在交叉,且差距很大,存在二阶共振的可能,因此对该齿轮—转子机构系统进行共振可靠性分析是必要的,这将是本文的后续研究工作之一。
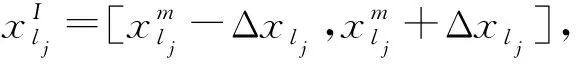

表4 齿轮—转子系统二阶固有频率均值的上下边界及相对不确定量
由表4可知,当原动机转动惯量、负载转动惯量和平均啮合刚度3个区间变量的波动系数ε同时取0.06时,齿轮—转子系统二阶固有频率的下边界相对不确定量为6.301%,上边界相对不确定量7.347%,其相对不确定量已经超出工程可接受的限值6%;当3个区间变量波动系数ε同时取0.1时,齿轮—转子系统二阶固有频率的下边界相对不确定量为13.738%,上边界相对不确定量为14.098%,远远超出工程可接受的限值。为此,本文需做进一步研究,研究二阶固有频率均值上下界随单个区间变量波动范围变化的规律。
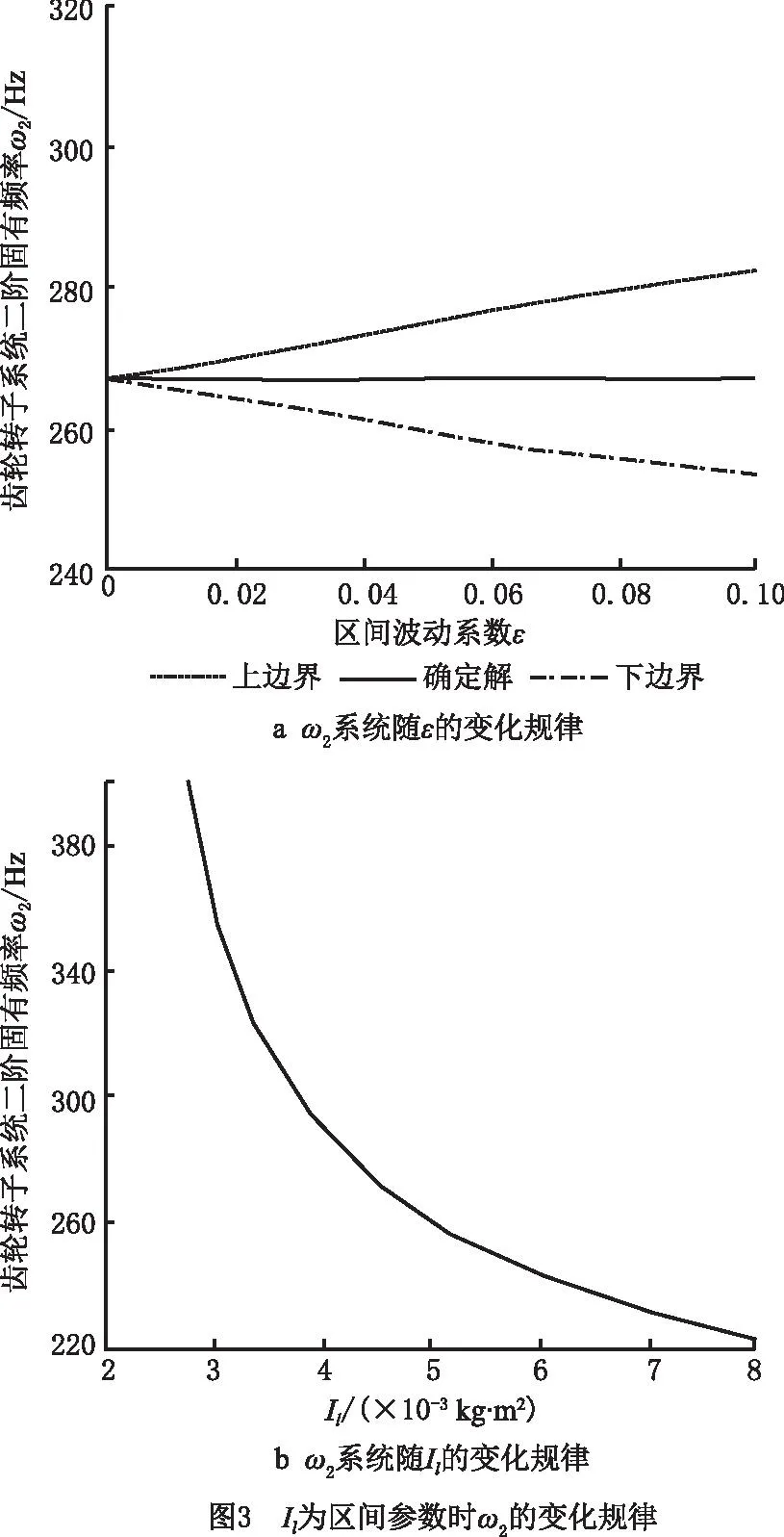
另外,3个区间变量的波动系数同时取[0,0.4]中的任意值时,齿轮—转子系统二阶固有频率不确定量均在工程可接受的限值之内,但无法获得单个区间变量波动对二阶固有频率波动的影响规律。为了研究单个区间变量对二阶固有频率波动的影响,逐一将3个变量中的两个变量取区间中值,另一单个区间变量波动系数ε从0取到0.10,获得原动机转动惯量Im、负载转动惯量Il和平均啮合刚度km分别为区间参数时二阶固有频率随区间变量波动系数ε的变化规律,以及随区间变量取值变化的规律,如图2~图4所示。


3.3 结果分析
由图2~图4可知,齿轮—转子机构系统的二阶固有频率ω2波动范围(波动区间宽度)随原动机转动惯量Im、负载转动惯量Il和平均啮合刚度km区间变量波动系数ε的增大而增大,基本为线性增加的关系;由图2b、图3b和图4b可知,二阶固有频率ω2随Im和km取值的增大非线性减小,随着平均啮合刚度km取值的增大非线性增大。
由图2a、图3a和图4a可知,当区间波动系数ε=0时,表示齿轮—转子机构系统各参数均为确定性变量,其二阶固有频率ω2=266.78 Hz。当Im为区间变量且区间波动系数ε=0.1时,二阶固有频率ω2的波动范围为[265.9,268.3]Hz,有效区间宽度为2.4 Hz,二阶固有频率ω2上下边界的相对不确定量分别为0.569 8%和0.33%,因此,仅当Im为区间变量且区间波动系数ε=0~0.1时,二阶固有频率ω2的波动范围在工程可接受的限值之内。当Il为区间变量且区间波动系数ε=0.1时,ω2的波动范围为[254.3,283.7]Hz,有效区间宽度为29.4 Hz,ω2上下边界的相对不确定量分别为6.342%和4.678%,上边界相对不确定量已超出工程可接受的限值;当km为区间变量且区间波动系数ε=0.1时,ω2波动范围为[258.5,270.2]Hz,有效区间宽度为11.7 Hz,ω2上下边界的相对不确定量分别为1.282%和3.104%,因此仅当km为区间变量且区间波动系数ε=0~0.1时,二阶固有频率ω2的波动范围在工程可接受的限值之内。综上所述,在实际工程中应严格控制负载转动惯量的波动区间。
由图2a和图3a可知,相对于二阶固有频率均值(确定参数下的值266.8 Hz),上边界随波动系数ε的变化较下边界大;由图4a可知,相对于二阶固有频率均值,上边界随波动系数ε的变化较下边界小。这种情况主要由变量的凸凹性导致。对于凸曲线函数,对称区间变量对应的函数值并不对称,而是上边界波动范围小于下边界;对于凹曲线函数,上边界波动范围大于下边界。
4 结束语
本文围绕随机—区间参数共存的齿轮—转子系统固有特性不确定性分析问题,提出一种基于区间随机阶矩技术的不确定性量化方法。该方法显性表征了含随机区间混合变量的齿轮—转子系统固有频率的近似解,推导了含混合参数的齿轮—转子系统固有频率的均值和标准差表达式,分析了区间参数影响系统响应和固有频率的规律。
(1)本文研究表明,考虑随机和区间变量共存时,齿轮—转子机构系统的固有频率为一个波动区间,且变量波动导致的固有频率区间并非关于确定性模型下固有频率中心对称,而是存在上下偏差,主要原因为变量的凹凸性。通过凹凸性、上下边界相对不确定量可以判断系统变量的波动规律,进而推断固有频率区间受变量波动影响的程度。当同时考虑多个变量存在区间波动时,系统固有频率区间的波动范围更大,甚至超过工程能接受的极限,因此设计分析时变量的区间波动性不可忽略。
(2)本文提出一种机构系统固有特性近似解的显式表征方法,避免了数值解方法求解动力学方程时的复杂计算迭代过程,提高了分析效率和计算精度。针对缺乏足够信息构建精确概率模型的齿轮—转子机构系统固有特性量化分析问题,本文提出基于区间随机阶矩技术的不确定性量化方法,该方法采用随机矩技术计算响应上下界的期望和标准差,并以上下界的期望为期望的上下界,以上下界的方差为方差的上下界,实现了对含随机—区间变量的机构系统响应不确定性的量化。通过对含随机和区间变量的机构系统深入地进行动力学研究,可为机械设备的可靠性分析及优化设计奠定基础。

