密度矩阵泛函理论及其计算方法
IRIMIA Marinela,王 坚
(1.湖州师范学院 国际学院,浙江 湖州 313000; 2.湖州师范学院 理学院,浙江 湖州 313000)
0 引 言
客观世界是由原子和分子组成的,它们遵从量子力学的规律.因此,原则上只要求解量子力学方程,就可以知道材料的各种物理化学性能.与实验比较,求解量子力学方程的计算成本轻,因此其已成为材料设计的重要手段.
一般的原子、分子和固体系统,其物理性质可通过求解下面的量子力学方程,即薛定谔方程来求解:
HΨ=EΨ.
采用原子单位,哈密顿算符H由以下几部分组成:
其中,第一项是电子的动能算符,第二项是原子核与电子间的库仑吸引势能,第三项是电子间的库仑排斥势能,第四项是原子核间的库仑排斥势能.假定波恩-奥本海默近似成立,即在考虑电子运动时,原子核可以看作是静止的,其原因是核比电子的质量大得多.对只有一个电子的氢原子,这一方程可以严格求解,且解的结果已被光谱实验完全证实,由此奠定了量子力学的基础.
对由两个电子或更多电子组成的原子、分子和固体系统,这个方程无法严格求解,只能通过近似方法求解.因为电子是费米子,波函数对于任意两个电子交换要具有反对称性.为满足这一性质,波函数Ψ可采用行列式的形式,因为行列式的两行或两列交换后,行列式值就变符号,正好符合反对称性要求.最简单的波函数形式是用一个行列式来表达的,这种方法也称为Hartree-Fock方法.为提高精确度,可采用多个行列式的线性组合来近似波函数,这种方法称为组态相互作用(简称CI).一个行列式对应一个组态,因此这是一种多组态的波函数方法.这在理论上是理想的,但随着电子数目的增加,行列式数目成指数式增加,因此这种方法很难推广到多电子系统.
20世纪50年代,人们认识到计算系统的能量不需要波函数的全部信息,只需要密度矩阵.例如,一阶密度矩阵的定义是[1]:
它是除了第一个电子的坐标外,对其余电子的坐标进行积分后得到的结果.每个电子有3个空间坐标和1个自旋坐标,积分包含空间坐标的积分和自旋坐标的求和.根据定义,它是厄米矩阵,因此可以对角化,本征值为实数,
其中,本征函数χi称为“自然轨道”;本征值λi称为自然轨道χi的占有数,0≤λi≤1.
因为电子是全同粒子,只要知道一个电子的动能,总动能就等于它的N倍.利用一阶密度矩阵,电子的动能可以简化为:

同样,原子核与电子的库仑吸引势能也可简化为单个电子的积分:
这里的γ(1,1)是γ(1′,1)的对角元,称为电子密度.
我们还可以定义二阶密度矩阵(或电子对密度):
它是波函数和它的复共轭中除了第一和第二个电子的坐标外,对其余电子的坐标进行积分后剩下的结果.其中,N(N-1)是电子对的总数目.电子间的库仑势能是两体算符,利用电子的全同性,只要考虑一对电子的库仑势能,然后乘上电子对总数即可,因此可以用Γ(1,2)来表示,即:
综上所述,与电子相关的能量可以用密度矩阵表示为:
因此,只要知道相当于密度矩阵γ(1′,1)和Γ(1,2)的信息,而不需要波函数的全部信息,就可以获得电子系统的能量.
1964年,Kohn和Hohenberg提出了密度泛函理论(简称DFT)[2].他们用反证法证明电子系统基态的能量是电子密度的泛函.然而这一定理只是个存在性证明,这个密度泛函的具体表达形式仍然未知.按照上面的分析,得出表1所示的结果.只有原子核与电子的库仑吸引势能可以用密度表达,电子能量的其余两项都不能用密度严格表达,所以只能寻找近似模型.Kohn和Sham最早通过均匀电子气体模型给出了一个称为“局域密度近似(LDA)”的泛函模型[3].固体中的电子运动近似均匀电子气体,因此这个模型在固体物理领域最先得到应用.但原子或分子中的电子密度一般是不均匀的,因此20世纪90年代,Perdew等对密度不均匀体系提出了“广义梯度近似”模型[4].DFT才开始在原子分子物理和化学领域得到应用.

表1 密度泛函方法与密度矩阵泛函方法的比较
1975年,Gilbert提出了密度矩阵泛函理论[5],这种理论用一阶密度矩阵作为泛函变量.与DFT方法比较,这一方法的优点是电子动能,以及原子核与电子的库仑势能都可以用一阶密度矩阵严格表达,只有电子间的库仑势能需要寻找泛函模型.密度矩阵泛函方法与密度泛函方法的比较见表1.从泛函模拟的角度看,这种理论方法比DFT更有希望.因此不少DFT学者,如M Levy、E K U Gross、E J Baerends等,都成为密度矩阵泛函理论的倡导者.
1 密度矩阵泛函
用CI波函数展开Γ(1,2),电子间的库仑势能可表示为:
其中,〈ij|kl〉为双电子积分.在波函数方法中,Γij,kl与轨道指标ij和kl所在的行列式的波函数展开系数有关.在密度矩阵泛函理论中,自变量是一阶密度矩阵,包括自然轨道χi及其占有数λi,因此原则上Γij,kl是自然轨道和占有数的函数.Γij,kl有4个下标,每个下标有M个轨道选项,因此Γij,kl共有M4项.如果轨道数M=10,那么就有1万个关于Γij,kl的泛函,这么多泛函逐个落实是不现实的.为使计算可行,泛函设计时常作近似处理,一般只保留指标为Γij,ij和Γij,ji的项,而忽略其他指标项,文献[6]中把这种泛函模型称为“JK”型.原本Γij,kl有M4项,实际模拟的只有M2项.
同时,由于双电子积分〈ij|kl〉已包含轨道,所以在设计Γij,kl的泛函模型时往往忽略轨道变量,而是假定Γij,kl只与占有数λi有关,这种简化的泛函模型称为“代数型”[7].
对实际的分子,我们用波函数推导的电子对密度对文献中发表的密度矩阵泛函进行逐项比较.结果发现,“JK”型和“代数型”泛函都不能重复从波函数得到Γij,kl,它们不具有一一对应的关系.这说明这些泛函模型都存在唯一性、对称性和普适性问题[7-8].
为了克服这些问题,经过长期的摸索,我们对以下形式的Γ(1,2)分解专门进行研究:
Γ(1,2)=γ(1,1)γ(2,2)-γ(1,2)γ(2,1)+λ(1,2),
其中,第一项是独立粒子引起的电子对密度,第二项是交换效应.这两项都可用一阶密度矩阵表达.后一项λ(1,2)称为“cumulant”,其对应的电子能量为:
著名DFT学者M Levy把Ecum称为密度矩阵泛函理论的关联能,它是能量泛函中唯一需要用泛函模拟的部分.因为关联能使能量降低,所以Ecum总是取负数.对Ecum进行模拟可避免模拟Γij,kl时符号的不确定性.这个符号的不确定性问题,文献中称为“phase dillema”[9].通过积分,Ecum隐含了所有可能指标ij,kl引起的贡献,避免了“JK”型和“代数型”泛函的近似性,也避免了模拟Γij,kl时有M4项之多的麻烦.
信息论之父Shannon曾提出,“信息熵”函数S=-∑ipilogpi可用来描述统计分布pi.我们将占有数分布λi看作一个统计分布,用S=-∑iλilogλi作为与这个分布相联系的信息熵,发现这个熵函数与关联能Ecum有较好的线性关系[10]:
Ecum=-κS-b,
其中,κ和b是与系统有关的常数,可以通过结合能、键长等理论或实验数据来拟合.按照这一表达式,当熵取最大值时,关联能达到最小值.关联能越低,意味着系统越稳定,这正是我们期望的,也是符合物理要求的.考虑到电子是费米子,应符合狄拉克-费米统计,信息熵的严格表达形式应为:
S=-∑i[λilogλi+(1-λi)log(1-λi)].
2 自洽场方程
Gilbert在提出密度矩阵泛函理论时,发现当占有数λi为分数时,轨道能级都是简并的[5].这一结果与实验或DFT计算的结果不符,他在文章中表示意外.因为能级简并,无法获得DFT那样的Kohn-Sham方程,计算时只能依靠非线性优化方法,计算效率很低.这一问题成为密度矩阵泛函理论的一个历史性问题.
用信息熵表达关联能后,系统的电子能量可表示为:
E=∑iλihii+Y-κS-b,
其中,与单电子有关的能量,hii=〈χi|h|χi〉,包括动能以及原子核对电子的库仑吸引势能,单电子算符h的定义为:
第二项Y包含双电子能量中可以用一阶密度矩阵表达的部分:
其中,
称为双电子积分.
考虑到自然轨道的正交归一性,以及占有数的求和性质∑iλi=N,我们用拉格朗日函数方法构造一个无条件优化的变分函数:
其中,μ和Λij是拉格朗日因子.
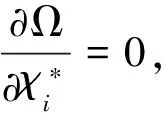
其中,算子Jj和Kj与Hartree-Fock方法中定义的库仑算子和交换算子完全一样,
为简化书写,定义算子:
这个算子与Hartree-Fock方法中的Fock算子比较,只多了系数λj.

(λi-λj)〈j|f|i〉=0.
若使这个方程成立,则f|i>应具有本征方程的形式,即:
fχi(1)=iχi(1).

〈i|f|i〉+κ[logλi-log(1-λi)]=μ.
利用〈i|f|i〉=i,可以解得:
编写量子力学计算软件是一项长期积累的工作.因为本文的本征值方程同Hartree-Fock方程非常接近,所以我们可以把Hartree-Fock程序作为出发点来开展研究.Hartree-Fock程序已研发了90多年,文献资料相当丰富,程序代码也很多,如原子的高斯基函数库、双电子积分、矩阵对角化等方面的内容.利用这些文献资料,可以大大加快新方法计算程序的编写.
Hartree-Fock方法是一个非常有效、稳定的计算方法.由于本征值方程的相似性,本方法也具有相当的稳定性、可靠性和可行性.在自洽场收敛方面,本文的方法比Hartree-Fock方法或DFT的Kohn-Sham方程更有优势,其原因是轨道占有数可连续变化,而在Hartree-Fock方法或Kohn-Sham方法中,占有数是跳跃性的,从1变成0或从0变成1,这容易使自洽场在收敛过程中,在近乎简并的轨道上发生跳跃,从而出现振荡现象而难于收敛.
3 计算举例:氢分子的分解
氢分子的分解问题是密度泛函理论的一个弱点,杨伟涛等曾专门在Science杂志上讨论这个问题[12].在DFT计算中,密度用轨道来展开,轨道上填充电子的方式按能级由低到高的次序来填充,有电子占据的轨道,占有数为1,否则为0.这一填充规则与Hartree-Fock方法一致,相当于用单个行列式表达波函数.在波函数计算领域,人们早就知道,单个行列式不能描述具有静态关联的系统,比如远离平衡态的氢分子.
图1为利用不同方法计算的氢分子能量随原子间距变化的结果.当氢分子分解成两个氢原子后,能量等于两个氢原子的能量之和,每个氢原子的能量是-0.5个原子单位,所以总能量应趋向于-1.由图1可知,Hartree-Fock(HF)方法、DFT的LDA泛函方法都没有收敛到正确的结果(-1),而本文的方法和CI方法都给出了正确的结果.因为在密度矩阵泛函理论中,轨道占有数λi可以为分数,这与CI波函数方法一样,所以它们的结果一致.这一结果说明,占有数可以为分数,密度矩阵泛函理论是一个比DFT方法更灵活、更完美、更精确的理论方法.对于四个氢原子组成的正方形结构和50个氢原子组成的一维分子链,我们也获得了类似的结果[13].
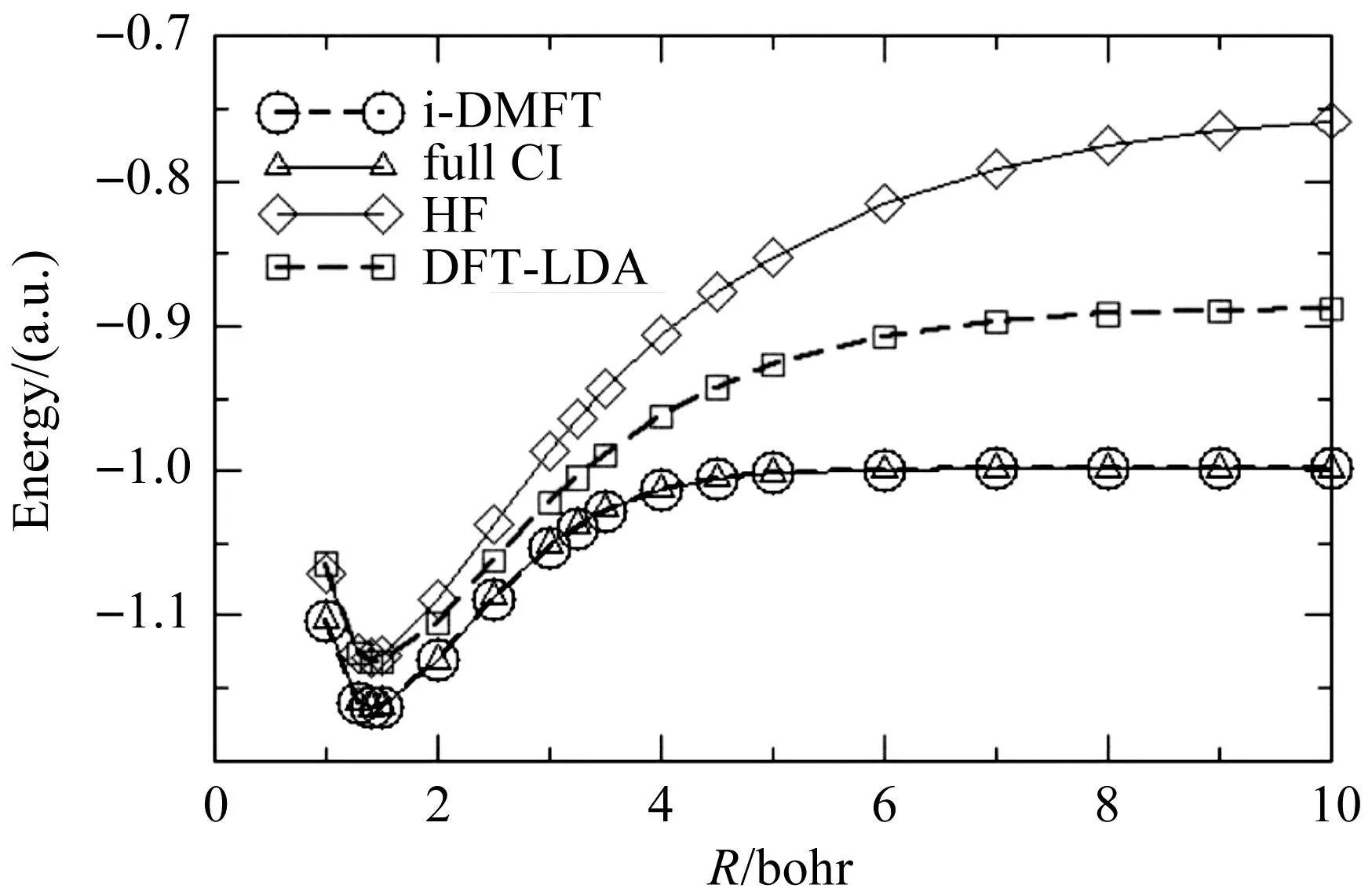
图1 氢分子分解过程的能量曲线
4 结 语
电子结构计算的核心问题是电子关联.在波函数计算方法中,电子关联是通过增加行列式数目来计算的,这种方法收敛很慢.而在密度矩阵泛函理论方法中,电子关联是通过轨道占有数来引入的.波函数方法目前只能处理10个左右电子的关联.在没有发现本征值方程前,密度矩阵泛函理论的计算采用非线性优化方法,计算量远比DFT的Kohn-Sham方法复杂.本文的本征值方程方法,使密度矩阵泛函理论的计算工作量相当于单个行列式的Hartree-Fock方法;在同样的计算机条件下,关联的电子数目可成千上万倍地增加.这为复杂分子的研究创造了条件,是一个历史性突破.
——《势能》

