Effects of drive imbalance on the particle emission from a Bose–Einstein condensate in a one-dimensional lattice
Long-Quan Lai(赖龙泉) and Zhao Li(李照)
1School of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China
2School of Electronic Engineering,Chengdu Technological University,Chengdu 611730,China
Keywords: Bose-Einstein condensate,particle emission,periodic drive
1.Introduction
Ultracold atomic experiments have become a versatile platform to extensively investigate quantum many-body systems during the past decades.Numerous advances enable the explorations on a wide range of interdisciplinary topics, such as novel quantum states,[1-3]nonequilibrium dynamics,[4,5]and quantum simulations.[6-8]In the out-of-equilibrium manybody physics,time-periodic driving is an exciting tool for coherently manipulating the interparticle interactions,[9]which provides new insights into topological states,[10,11]synthetic gauge fields[12]and modulated lattices,[13-16]and leads to some striking phenomena,e.g.,the stimulated particle jets resembling fireworks.[17]
In that visually appealing experiment, researchers periodically modulated the magnetic field near the Feshbach resonance,[18]and hence made the scattering length of the atoms in the condensate oscillate sinusoidally.Pair of excited atoms shared half of the drive energy,and escaped from the trap in antipodal directions, resulting in significant particle jets.Such amplification offers stimulating applications in quantum metrology and simulation of highly nonequilibrium systems.Subsequently, a number of experimental and theoretical groups have performed a series of follow-up investigations and revealed various new aspects,[19-26]e.g., the jet substructure in nonuniform and rotating condensates[20]and correlated jets from a driven matter-wave soliton.[22]In particular, semi-infinite and infinite lattice models were introduced to mimic the behaviors of the trapped particles in a transparent way,[27,28]where the time evolution of the atoms in the horizontal plane was simulated by the hopping of particles from the condensate to the “leads” and between neighboring sites,and the spatial expansion was simply limited in one dimension.
Simultaneous manipulations were often employed to the condensates in generic studies, while it might be interesting to separately vary the drives.In some other contexts, timeperiodic drivings with tone-varying frequencies were applied,such as pattern formation in a driven condensate,[21]topological Floquet engineering and pumping in optical lattices.[29-31]In a previous work, we analyzed a minimal one-dimensional lattice model where the trap contains two sites, and periodically modulated the interparticle interactions to study the parametric resonance of particle emission from a Bose-Einstein condensate.[28]We now turn to a similar system, however,with periodic drives that are separate in modulation amplitudes and relative phases, and follow the perturbative framework developed in Ref.[28]to explore the collective emission of particles.We discuss various cases with different modulation amplitudes and relative phases,where imbalanced drives may result in the distinct enhancement of the emission and the redistribution of energy bands.For clarity, we also give intuitive illustrations of the influences.
The paper is organized as follows.In Section 2, we introduce the two-site lattice model and discuss the formalism of dealing with such a system.In Section 3, we present the numerics and discussions based on perturbative analysis, and compare different cases of drives by varying the modulation amplitudes and relative phases,respectively.Finally,we summarize our results in Section 4.
2.Theoretical model
We consider the situation of a one-dimensional infinite lattice, where a local trapping potential of depthVis applied to confined the Bose-Einstein condensate,as shown in Fig.1.Two central sites,labeledaandb,are coupled with amplitudeJab, which allows the transfer of atoms from one site to the other.When the perturbations are turned on,excited particles with sufficient energy can escape from the trap and travel to infinity, by hopping onto one of the two leads with coupling strengthJcand moving between nearest-neighbor sites with amplitudeJl.The Hamiltonian is thus written as
where ˆaj≥1and ˆbj≥1are the annihilation operators for the left or rightj-th site, and ˆa0and ˆb0correspond to the locally trapped central sites.A constant termUcharacterizes the time-independent on-site particle interactions, whilega(t)=gasin(ωt)θ(t)andgb(t)=gbsin(ωt-φ)θ(t)are the periodic drives exerted to each site,withga,brepresenting the drive strengths,ωthe drive frequency,φthe relative phase,andθ(t)the step function.
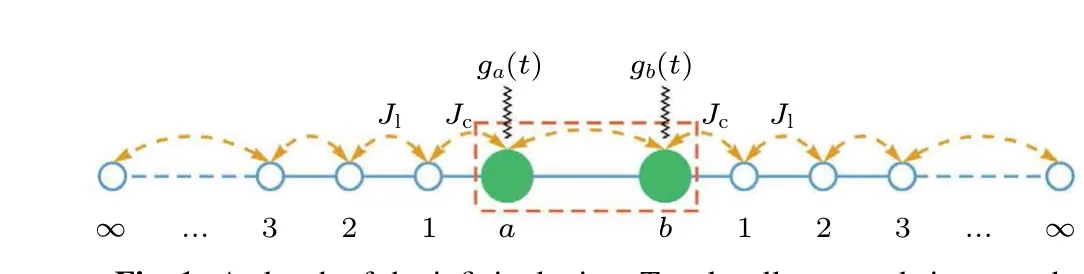
Fig.1.A sketch of the infinite lattice.Two locally trapped sites a and b are coupled, which enables atoms to tunnel back and forth, and the pairwise interaction of atoms on these two sites has strength U.The red dashed box indicates the local trap, and the sites on each lead are labeled by 1,2,3,...,∞.
Such an inhomogeneous lattice model with spatially localized interactions can be implemented in an experiment by the literal combinations of optical lattices and microtraps,[32]where one could routinely engineer an array of Bose-Einstein condensates in the lattices with a trap and barriers confining the central sites, and modulate the time- and spacedependent interactions through magnetic field driven Feshbach resonances.[17,18]Our work, however, is not a proposal for a particular experiment.Nevertheless,we provide a simple model whose exploration gives insight into the observations made in a more complicated study.
The formalism of such a system can be developed along the same lines as in previous works.[27,28]We introduce, in the context of mean-field approach, the expectation values ofaj≥0=〈ˆaj≥0〉 andbj≥0=〈ˆbj≥0〉, where their squares represent the number of particles on sitej.In the fireworks experiments,[17,19-22]the average dc scattering lengths were generally kept small, and in a previous work we have demonstrated that a finiteUdid not qualitatively change the results,[27]thus we take the limit ofU=0 for simplicity.We begin from the equilibrium atg=0,which leads to the Heisenberg equations of motion foraj≥0(taking units where ¯h=1)
Analogous equations are straightforward forbj≥0.To largely simplify the analysis,we deal with the above equations at the perturbative level,where the drive strengthgand the coupling strengthJcare both small.The substitution of the ansatz ofa0=αe-iνtandaj>0=αe-iνte-κ1 e-κ(j-1)into the equations results in coshκ=ν/(-2Jl) andκ1=-ln[-Jc/(ν+Jle-κ)],and we obtain two discrete modes of the system corresponding to the energies ofν-=V-Jabandν+=V+Jab,respectively.
To observe significant particle emission, there are some restrictive conditions.The infinite lattice acts as a bath,whose spectrum is a continuum corresponding to-2Jl<ν <2Jl.The periodic drive provides the required energy for pumping particles to the excited state, such that they can escape from the trap into the continuum.We need to be in the regime where the modeν-=V-Jabis stable while the modeν+=V+Jabis damped,which requires|V-Jab|>2Jland|V+Jab|<2Jl.Specializing to the case ofV=-|V|<0, we reach the constraints for the trapping potential as-Jab <|V|-2Jl<Jab.
We subsequently eliminate the leads by writinga1(b1)as a function ofa0(b0).As a result, one can focus on the time evolution of the trapped particles, and a set of nonlinear integro-differential equations for the central sites are available,
whereGj1(t) = ij-2jJj(2Jlt)θ(t)/Jltis the time-domain Green’s function withJn(z) being the Bessel function of the first kind.[27]To describe the nonlinear dynamics of the system, one can directly solve Eq.(2)through Eq.(4), while we obtain the following results mainly by perturbatively solving Eqs.(5) and (6), which is applicable for small parameters of the drive strengthgand the coupling strengthJc.
3.Results and discussion
We assume that the parametric drive is exerted at timet= 0.Without any loss of generality, we induce an initially slight difference ofa0andb0, i.e.,a0(t= 0) = 1.01 andb0(t=0)=1, to seed the system at the lowest mode ofν-=V-Jab, and explore the nonlinear dynamics when the drives are varied.We also take the unitsJab=1 in most of our numerical calculations, while reintroducing the scaleJabin discussions as appropriate.There is a typical threshold for the drive strength,[28]thus only those amplitudes above the threshold are taken into account.To keep simplicity, we restrict ourselves to the short-time behavior of the trapped particles,which is sufficient for the current study,and present certain situations with typical relative phases.
3.1.Relative phase φ =0
3.1.1.Same drive strengthga=gb
We first consider the general case with equal drive strengthga=gb=gand relative phaseφ=0.As shown in Fig.2, the drive strengthg=0.05 is still too small to induce significant emission within this short time.When the amplitude is increased, for generic frequencies the system keeps very stable with few trapped particles ejected.Once the frequency is tuned toω=4Jab,the pulses are visible at intermediate times,and we term it as the“resonant frequency”.Fromg=0.1 we immediately recall the two-site model,[28]while intermittent emission emerges when the drive strength is further increased tog=0.2 andg=0.3,which was discussed in detail in Ref.[33].
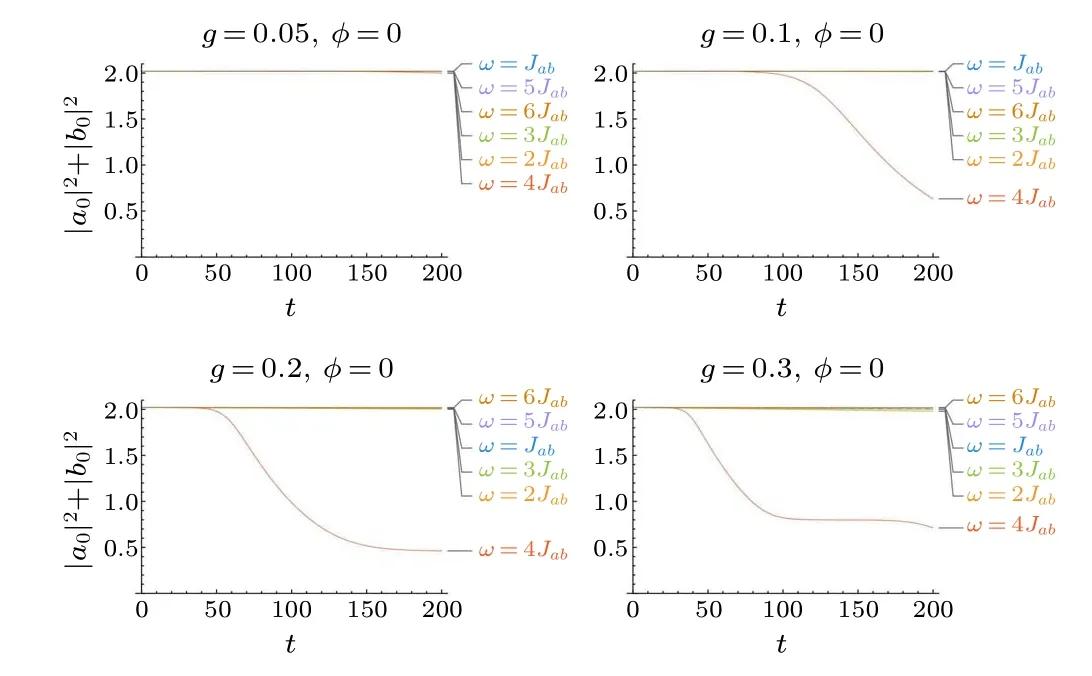
Fig.2.Time dependence of the number of particles in the central sites|a0|2+|b0|2 for equal drives g=ga=gb,under various frequencies ω.Here, the trapping potential is V =-2, and the coupling strengths are Jc =0.1 and Jl =1.Energies are in units of Jab and times are in units of ¯h/Jab.
3.1.2.Eliminating one of the drives
Next, we eliminate one of the drives by taking strengthgb=0 and vary the other onega,which means that the manipulation is simply applied to sitea,and we use Δg=ga-gb=gato denote the imbalance of modulation amplitude.Figure 3 plainly demonstrates the distinct enhancement of particle emission that even a small imbalance of Δg=0.05 is available for a remarkable jet,and the principal frequency becomesω=2Jabinstead ofω=4Jabunder different imbalances.For Δg=0.05 and Δg=0.1,only the resonant frequencyω=2Jabgives rise to prominent emission, and the jet emerges much earlier than that of the cases in Fig.2.At intermediate times 50<t <150, the number of trapped particles|a0|2+|b0|2rapidly decays, leading to a large pulse until very few particles are left.For larger amplitude imbalances of Δg=0.2 and Δg= 0.3, the frequencyω= 4Jabcomes into effect, whileω=2Jabresults in intermittency.Note that there would be another frequency ofω=Jabwhich can induce a slight decay within this short period of time.
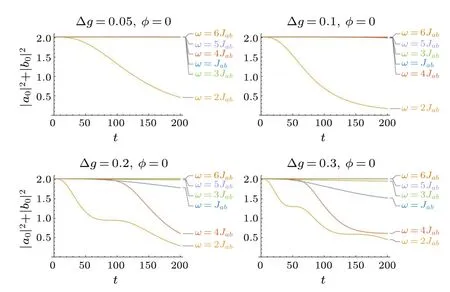
Fig.3.Time dependence of the number of trapped particles for imbalanced drives Δg=ga under various frequencies ω with fixed gb =0.Here,we have taken V =-2,Jc=0.1,and Jl=1.Energies are in units of Jab and times are in units of ¯h/Jab.
Since we present, for simplicity, particular integer frequencies in the above analysis to show the main properties of the particle emission,here we takeg=Δg=0.3 as examples to sweep the frequency.Figure 4(a)shows that for equal drive strengthsg=0.3 and relative phaseφ=0,a distinct peak appears atω=4Jab,which leads to the most significant particle emission.There is actually a narrow resonance,where the excited atomsNecorresponding to the frequencies in between are definitely nonzero.As a comparison in Fig.4(b), for the case with Δg=0.3 andφ=0,the adjacent area is somewhat narrower, while a new peak with typical “bandwidth” shows up atω=2Jab, and a fairly sharp but small peak emerges atω=Jab.
Under the circumstance ofga=gb=g,particles in sitesaandbare simultaneously driven and they can be treated as a whole, in which the modes and energy levels are spectrally separated,as briefly depicted in Fig.5(a).For generic drives,particles in the central sites are not directly ejected, but that promoted from the ground state ofν-=V-Jabto a higher energy level ofν+=V+Jab, namely a build-up stage at the beginning.[33]Pairs of atoms are excited at a time, and they share half of the drive energy before escaping from the trap and moving off along the leads.To this end, we need the appropriate principal frequency that satisfies the energy gap ofω=2(ν+-ν-)=4Jab, which corresponds to the peak in the spectrum,and there is a typical“bandwidth”that takes the levelν+=V+Jabas the center line.
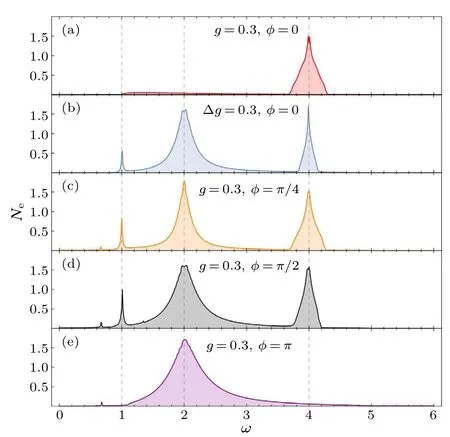
Fig.4.Number of the excited atoms Ne versus drive frequency ω.Here, Ne is calculated from (|a0(t = 0)|2+|b0(t = 0)|2)-(|a0(t =te)|2+|b0(t =te)|2) up to time te =200, and gb is set to be 0 with Δg=ga-gb =0.3.We have taken V =-2, Jc =0.1 and Jl =1, and the frequency step is Δω =0.01.Energies are in units of Jab and times are in units of ¯h/Jab.
As for the case of Δg=ga, due to the elimination of the drive on siteb, only particles in siteaare subsequently stimulated when the perturbation is turned on.Sitebplays the role of a“source”via the coupling, and the amplitude imbalance motivates energy shift and redistributes the energy bands,as outlined in Fig.5(b).To be specific, under a suitable frequency aroundω=2Jab,half-pairs of atoms are excited from the ground state ofV-Jabto the higher energy level ofV,which takes a much shorter time in the build-up stage and emits more particles than the former case.Since the drive can provide energy in multiples, we still have another main frequencyω=4Jabthat corresponds to the level ofV+Jab,but the“bandwidth”becomes narrower.The system emits a small portion of particles from the ground state to the energy level ofV-Jabunder an approximate frequency ofω=Jab, by pumping single atom at a time.
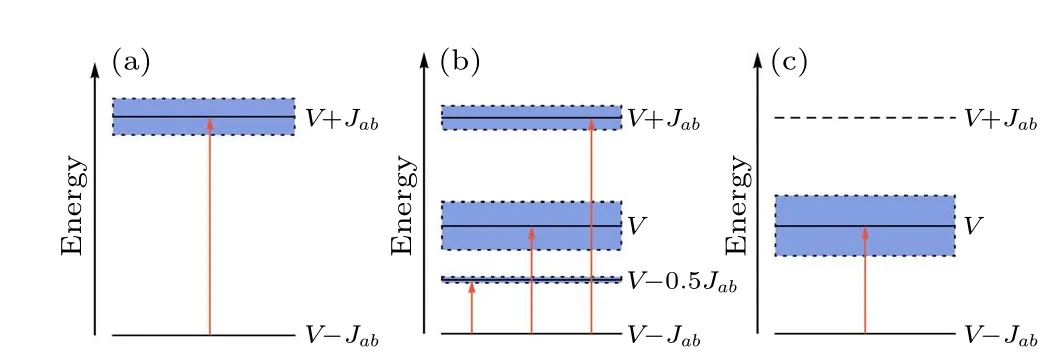
Fig.5.Sketch of the “band structure” for cases: (a) ga =gb =g and φ =0, (b) Δg=ga and φ =0, (c) ga =gb =g and φ =π.The blue regions indicate the dominant“bands”.
From a more insightful point of view, basically the initial state with (a0,b0)≃(1,1) is symmetric.When the same driving fieldsga(t)=gb(t)are applied to the central sites,the whole Hamiltonian holds a reflection symmetry that the state should maintain during the time evolution.As a consequence,the state (1,1) can only evolve towards (0,0), and the particle emission are typically in pairs.If one breaks the reflection symmetry, i.e., either the modulation amplitudes or the relative phases of the driving fields applied to the two central sites are imbalanced,the emission of a single particle becomes possible.
3.1.3.Fixing drive strengthgb=const.
We further fix one of the drive strengthsgb ̸= 0 while varying the other onega.In particular,we keepgb=0.3 and present some positive Δg′=ga-gbin comparison,where sitebis driven persistently but the rate of particle promotion from each site varies.In this situation,the system shares similar decay properties with the former case,as shown in Fig.6.However,when the amplitude imbalance is as small as Δg′=0.05,there are two main frequenciesω=4Jabandω=2Jabthat give rise to significant jets.They take almost same times to result in particle jets, but frequencyω=4Jabcan cause intermittency, which is somewhat different from Fig.3.When the imbalance is Δg′=0.1, the principal frequency gradually turns intoω=2Jaband under frequencyω=Jabthe system can also emit a fraction of particles.In addition, if the imbalance is further increased to Δg′=0.2 and Δg′=0.3, the frequencyω=Jabwould induce intermittency as well.
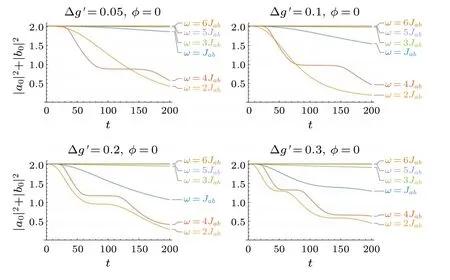
Fig.6.Typical examples of the time evolution of the trapped particles for different Δg′=ga-gb under different frequencies ω with fixed gb =0.3.Here,V =-2,Jc =0.1,and Jl =1.Energies are in units of Jab and times are in units of ¯h/Jab.
3.2.Relative phase φ ̸=0
Phase difference often plays an important role in nonequilibrium quantum dynamics.In the above considerations, we neglect its influence by simply taking the relative phase asφ=0.Here, we reintroduce that the driving applied to sitebholds a relative phase discrepancy when the perturbation of siteais turned on, while keeping the drive strengths asga=gb=g=0.3.We scan the frequency and calculate the number of excited atoms on each site,and present the comparisons among some typical relative phases ofφ=π/4,π/2 andπ,as shown in Figs.4(c)-4(e).
Compared to Fig.4(a) one can plainly see that the nonzero relative phaseφ ̸=0 makes the “bandwidth” at frequencyω=4Jabbecome thinner,while it opens another band at frequencyω=2Jab, which turns to be wider as the phase difference increases fromπ/4 toπ/2.When the relative phase isφ=π, the peak at frequencyω=4Jabvanishes, and there is only a distinctly wide band around frequencyω=2Jab, as depicted in Fig.5(c).It is interesting to note that these two cases with relative phasesφ=π/4 andφ=π/2 share similar properties to that of the situation with amplitude imbalance Δg=0.3 and relative phaseφ=0, which means that in experiments one can probably, based upon demand, manage to induce analogous effects by generating either amplitude imbalance or phase difference.drive frequencyω=2Jab,by plotting the number of particles on each site in the left or right lead.
4.Conclusions
We have introduced a one-dimensional infinite lattice,in which the trap confines two central sites, and studied the influences of drive imbalance on the collective particle emission from a Bose-Einstein condensate.We follow the formalism developed in previous works to parametrically modulate the particle interactions,while separately varying the periodic drives in modulation amplitudes and relative phases.
Within perturbative analysis and numerical calculations,we find that the modulation amplitude imbalance may result in the enhancement of particle emission and redistribute the band structures,where even a small drive gives rise to significant particle jets,energy shift and band broadening.Moreover,relative phases can lead to similar band gaps,where the effect induced by nonzero phase difference is basically analogous to that of the modulation amplitude imbalance.One can thus,for certain purpose,employ either method in precise quantum manipulations in experiments.
There have been a number of recent explorations with respect to two-frequency phase modulations[21,29-31]both in one and two dimensions.The geometry of the system and the boundary condition typically play a role in the excitations.If one explicitly follows the methodology, the dynamics of the lattice systems would be particularly interesting.Such influence of parametric drives with varied frequencies on distinct configurations is worth investigating, and we leave it for future research.
To be more explicit, for relative phaseφ=0 sitesaandbare driven simultaneously by same drives,such that one returns to the general case ofga=gb.As for nonzero phases,e.g.,φ=π/4,there has been a difference between the two separate drives.They deviate fromga(t=0)=0 andgb(t=0)=and then Δg(t)φ=π/4=sin(ωt)-sin(ωt-π/4),which is in fact the situation of the former case with Δg=ga-gbin Fig.3.Therefore,under these two cases the system shares similar characteristics,and the amplitude imbalance Δggrows with the increase ofφ ≤π/2.Once the relative phase is tuned toφ=π, the resulting amplitude imbalance Δg=ga-gb=2sin(ωt) is twice of the generic case, leading to the shift of the main frequency fromω=4Jabtoω=2Jab,as well as the broadening of the bandwidth.As a specifically visible example, we present in Fig.7 the intermittent antipodal jets under
Acknowledgments
Project supported by the China Scholarship Council(Grant No.201906130092), the Natural Science Research Start-up Foundation of Recruiting Talents of Nanjing University of Posts and Telecommunications(Grant No.NY223065),and the Natural Science Foundation of Sichuan Province(Grant No.2023NSFSC1330).
——龙泉宝剑锻制技艺
- Chinese Physics B的其它文章
- Does the Hartman effect exist in triangular barriers
- Quantum geometric tensor and the topological characterization of the extended Su–Schrieffer–Heeger model
- A lightweight symmetric image encryption cryptosystem in wavelet domain based on an improved sine map
- A new quantum key distribution resource allocation and routing optimization scheme
- Coexistence behavior of asymmetric attractors in hyperbolic-type memristive Hopfield neural network and its application in image encryption
- Effects of connected automated vehicle on stability and energy consumption of heterogeneous traffic flow system

