基于深度算子神经网络的翼型失速颤振预测1)
席梓严 戴玉婷 , 黄广靖 ,2) 杨 超
* (北京航空航天大学航空科学与工程学院,北京 100191)
† (天目山实验室,杭州 310023)
引言
动气动弹性问题是指非定常气动力和柔性结构之间相互耦合作用导致的稳定性/动响应问题,具有重要的研究价值:一方面气动弹性动响应可以用于振动俘能,张野等[1]利用翅片超表面将涡激振动转变为驰振,显著提升了俘能性能;另一方面动气动弹性会带来结构的大幅振动,导致飞行器结构破坏,比如失速颤振现象[2].失速颤振是弹性结构在初始大迎角下产生的一种单自由度自激振荡现象.失速颤振主要出现在直升机旋翼与涡轮叶片中,大迎角飞行、强阵风等情况下亦有可能诱发机翼失速颤振.与经典弯扭耦合颤振不同的是,失速颤振过程伴随着大尺度的流动分离与再附[3],气动力非线性程度高,因此对于失速颤振失稳速度和振荡幅值的高精度高效分析十分重要.Dimitriadis 等[4]开展了二自由度翼型风洞试验研究,测量了失速颤振的分岔速度.Bhat 等[5]采用能量理论对失速颤振边界进行了辨识.Poirel 等[6]在转捩雷诺数下进行了失速颤振风洞试验,研究了雷诺数对失速颤振特性的影响.
随着计算流体力学(computational fluid dynamics,CFD)仿真技术的发展,CFD 被逐渐运用于动态失速与失速颤振研究中.Spentzos 等[7]基于CFD 方法对三维机翼动态失速特性进行了仿真研究;Yabili 等[8]基于OpenFOAM 开发了一流固耦合求解器,仿真求解二维翼型失速颤振问题.目前针对二维翼型在不同雷诺数下的失速颤振速度和极限环幅值多采用CFD 仿真进行研究[9-11].然而,对于失速颤振等流固耦合研究而言,CFD 方法存在计算时间长、迭代繁琐等问题.为克服这些缺点,提出了非定常气动力降阶模型[12-15],旨在尽量保证精度的前提下提高计算效率.
降阶模型可分为线性模型与非线性模型两种.线性模型包括自回归滑动平均模型[16-17]、Volterra级数模型[18]等,对于线性或弱非线性气动力建模有着良好的效果.然而对于动态失速这类强非线性数据,则需要采用以神经网络为代表的非线性数据驱动降阶模型[19-21]进行建模.Wang 等[22]建立了基于多保真度数据的机器学习框架,对动态失速气动力进行机器学习建模,展现了较好的泛化能力.对于时域非定常气动力而言,为时序数据所设计的循环神经网络(recurrent neural network,RNN)也具有良好的效果.Mohamed 等[23]开展了二维翼型动态失速试验,并采用双向长短时记忆(long short-term memory,LSTM)神经网络对实验数据进行学习与预测,结果证明双向LSTM 能够捕捉极端迎角下翼型非定常气动力的物理特性.Dai 等[24]使用门限循环单元(gated recurrent unit,GRU)的循环神经网络对翼型动态失速气动力进行学习,并基于所建立的降阶模型进行了失速颤振幅值与分岔速度预测,获得良好效果.Li 等[25]采用LSTM 神经网络对二维翼型非定常气动力进行学习,并进行气动弹性响应预测.Dou 等[26]同样基于LSTM 建立了二维翼型非定常气动力降阶模型,与结构动力学方程进行耦合,预测跨音速抖振现象.
Lu 等[27]基于算子学习的理念,提出了深度算子神经网络.深度算子神经网络基于数据对线性或非线性算子进行学习,具有收敛速度快、泛化能力强的优势,被用于求解微分方程[28]、边界层不稳定波[29]和裂纹扩展[30]等问题.同时,深度算子神经网络具有极强的可扩展性,其包含的两个子网络可根据需要选择合适的类型.Lu 等[31]就提出了深度算子神经网络的多种扩展形式,在Burgers 方程、对流问题、可压缩Euler 方程和小幅俯仰振荡翼型表面涡强度等算例上对这些扩展形式进行验证,表明采用适当扩展形式的深度算子神经网络能够在多种问题中表现出良好的精度.Garg 等[32]将动态系统的输入变量与时间变量分别输入深度算子神经网络的两个子网络,对动态系统的时序响应进行学习与预测.
基于以上背景,本文基于研究[24]数据,将GRU 和LSTM 两种单元与深度算子神经网络相结合,进行动态失速非定常气动力建模与失速颤振预测.本文对研究[24]中神经网络的结构进行更改,以获得更高的预测精度,并对其中的机理进行了初步的分析.
1 基于深度算子神经网络的非定常气动力数据驱动模型理论
传统神经网络学习的是数据I到数据O之间的函数关系K
与之不同的是,深度算子神经网络学习的是从函数u(x) 到函数v(y) 的映射关系 G[27]
式中 G 即为算子.深度算子神经网络中包含了branch net 与trunk net 两个子网络,分别以u与y作为输入.若u为连续函数,则需要将其在定义域中取点集[x1,x2,···,xn],采样为离散值 [u(x1),u(x2),···,u(xn)] 作为branch net 的输入向量.采样点的分布可根据需要进行选择,但需在所有的输入函数上保持一致.两个子网络的输出向量分别定义为D=[d1,d2,···,dl]T与F=[f1,f2,···,fl]T,D与F做内积,并加上一偏置量b0,便得到深度算子神经网络的输出
为便于理解,在此以积分算子为例,对深度算子神经网络的输入输出结构进行说明.定义一积分算子 G,采用深度算子神经网络对其进行学习.满足
其中u(x) 为输入函数(被积函数),y为原函数的自变量.在此取u(x)=2x,则原函数为G(u(x))(y)=y2.设u(x) 定义域为 [ 0,1],在定义域上以平均间隔取20 个点 [ 0.05,0.1,···,1] 对u(x) 进行采样,得到采样集[0.1,0.2,···,2] .原函数的定义域同样为 [ 0,1],在该域上随机取100 个点 [y1,y2,···,y100],计算原函数的值,与采样集一同构成训练集,见下式
其中branch net 的输入维度为20,与采样集相匹配;trunk net 的输入维度为1,与原函数的自变量维度相匹配.在训练集上对深度算子神经网络进行训练,便可得到如图1 所示的结果.

图1 积分算子的神经网络训练结果Fig.1 Training result of integral operator
深度算子神经网络的branch net 与trunk net 多为多层感知器(multilayer perceptron,MLP)神经网络.而在本研究中,考虑到非定常气动力的长时滞与强非线性特性,选择GRU 与LSTM 两种神经网络单元的RNN 作为branch net,而trunk net 则为MLP神经网络,形成了GRU-DeepONet (后称为G-Deep-ONet)与LSTM-DeepONet (后称为L-DeepONet).
本研究中,深度算子神经网络的输入为长度l的迎角序列 α=[ αn-l+1,αn-l+2,···,αn] 与相对时刻指示标量t,输出为在给定迎角运动下相对时刻t处的俯仰力矩系数Cm
其中,α 直接与时滞效应相联系,因而作为branch net 的输入.t则作为trunk net 的输入,取值范围为[0,1],是时间步的归一化表示.由于t的存在,深度算子神经网络所学习和预测的时间步范围 [t1,t2] 构成一组超参数,本研究中该范围设定为后1/2 时间步,即t1=n/2,t2=n,l=50 .
branch net 中的RNN 网络均为两个隐含层,每层神经元个数为100.trunk net 均为3 个隐含层,每层神经元数量为100,激活函数 σ 为tanh.所构建的深度算子神经网络结构如图2 所示.同时,加入了只有GRU 与LSTM 的两组传统RNN 作为对照,以 α为输入,最后一个时间步的Cm为输出,网络结构与branch net 保持一致.
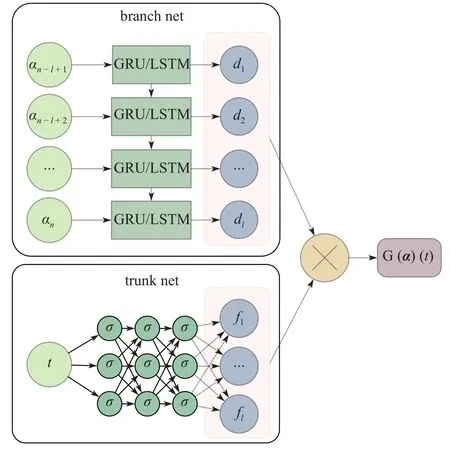
图2 深度算子神经网络结构Fig.2 Structure of DeepONet
2 基于深度算子神经网络的翼型俯仰振荡气动力预测结果与分析
研究对象为NACA0012 翼型,在训练信号驱动下进行俯仰运动,进行CFD 计算得到相对应的气动力系数,来流速度固定为8 m/s.使用的训练数据与文献[24]相同,训练输入信号为一正弦叠加形式的信号
其中,Ai为随机选择的大幅值,且最大值大于失速颤振极限环振荡幅值,T为绝对时间.通过CFD 计算得到在如式(7)俯仰运动下NACA0012 翼型的俯仰力矩系数Cm,如图3 所示.

图3 训练数据集Fig.3 Training dataset
同时,所有的数据均进行了z-score 标准化处理[33]以提高训练速度,见下式
其中y为原始数据,与s分别为y的均值与标准差.y∗ 为标准化处理后的数据,其均值为0,标准差为1.
采用Adam 算法对几种神经网络进行训练,初始学习率设置为0.001,并使用余弦退火方法[34]进行动态调节,以进一步提高模型的收敛性与泛化能力.损失函数为均方误差MSE (mean squared loss).为更直观地监控训练过程,采用误差e作为判定收敛的标准,其定义见下式
其中Cm,NN为神经网络预测值,Cm,CFD为CFD 计算值,二者均为多个不同时间点的Cm值所拼接的矢量;式中范数为F范数.采用RTX3090 GPU 进行训练,过程中的误差曲线见图4,待误差小于10%并稳定后完成训练.在相同误差水平上,深度算子神经网络训练所需迭代次数为200 次左右,小于普通循环神经网络的400 次.但在训练总时长方面,深度算子神经网络进行一次训练所需时长为 2580 s,高于RNN的 721 s .

图4 训练过程Fig.4 Training process
对训练后的几种气动力数据驱动模型进行泛化测试.选取了不同幅值与不同减缩频率的正弦俯仰信号进行CFD 仿真计算,作为泛化测试的测试数据,测试结果见表1、图5 和图6.表1 中减缩频率k的定义为k=ωc/(2U),式中 ω 为正弦信号圆频率,c为弦长,U为来流速度.图5 是对表1 所列相对误差的统计,可见对于同一类型的RNN,trunk net 的加入使得泛化误差平均值与中位数均降低了3%左右.同时,虽然最小误差有所提高,但误差的分散性大幅降低.可以认为深度算子神经网络具有更好的泛化能力.而结构更复杂的LSTM 则比GRU 更好地捕捉到了气动力中的非线性特征,体现在LSTM 与LDeepONet 平均泛化误差均低于GRU 与G-Deep-ONet.深度算子神经网络与RNN 最大的区别在于对时间进行编码的trunk net,因而取训练完成后的GDeepONet,进一步对trunk net 的作用进行研究.
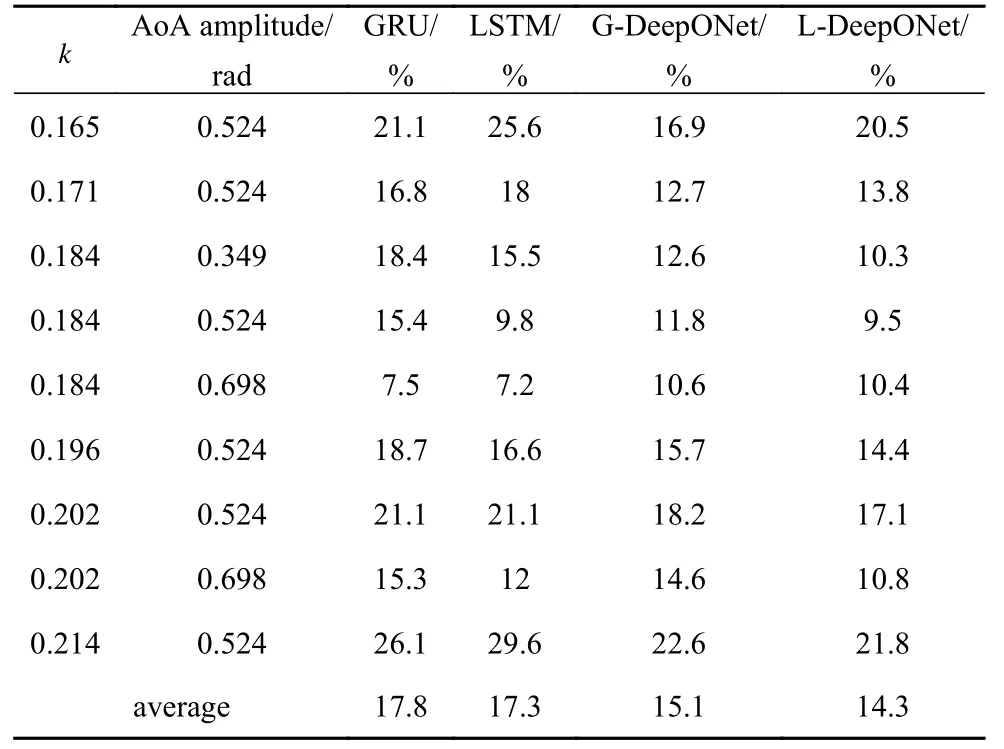
表1 泛化误差Table 1 Generalization error

图6 部分工况泛化测试结果Fig.6 Generalization test results
根据式(3),trunk net 的输出向量F与branch net的输出向量D进行了内积,这一过程可以认为是对D的各分量进行了加权求和,fi为di的权重.图7 展示了fi的绝对值随t的变化情况,fi绝对值越大,则权重越高.由第1 节所述,当t=0 时,深度算子神经网络的输出值为绝对时间第n/2 步时的气动力系数,对应i=25 ;当t=1 时,则对应i=50 .能够发现,上述两点之间存在一条明显的高权重带,说明与t所对应的fi值具有最高的权重;此外,图中也存在其他规律性的结构,说明深度算子神经网络所输出的气动力以t所对应的di值为主,并采用其他时间处的di值进行微调,在深度算子神经网络中体现了气动力的时滞特性,因此比普通RNN 提升了精度.

图7 | fi| 随 t 与 i 的变化Fig.7 | fi| heatmap
进一步对branch net 的输出向量D进行拼接,并与CFD 计算的气动力系数Cm进行对比,二者均进行了z-score 标准化处理,结果见图8,能够发现D与CFD 结果具有一定的相似性.可以认为,D与Cm具有相似的物理含义,而D通过与F内积进行权重调整后得到了高精度结果.

图8 D 与CFD 计算值的对比Fig.8 Comparison between D and CFD results
3 基于气动力数据驱动模型的失速颤振极限环预测与结果分析
单自由度二元翼型气动弹性模型如图9 所示.其气动弹性方程如下
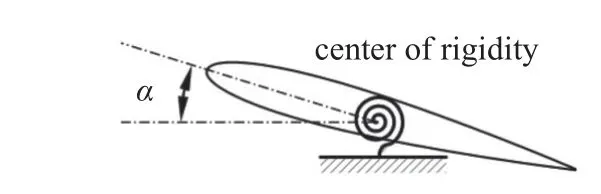
图9 单自由度二元翼型气动弹性模型Fig.9 Aeroelastic model of single-degree-of-freedom airfoil
其中,Iα为转动惯量,Cα,ζ 与Kα分别为阻尼系数、阻尼比与刚度系数,M为俯仰力矩.c与b分别为翼型的弦长与展长,U为来流速度,这些参数取值与文献[24]保持一致.将式(10)写为状态空间的形式,即下式,即可通过龙格-库塔方法进行求解
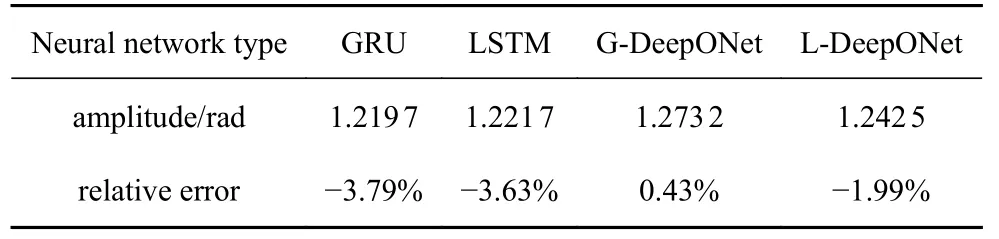
表2 失速颤振预测极限环振荡幅值Table 2 Predicted amplitude of stall flutter

图10 8 m/s 极限环振荡预测结果Fig.10 Stall flutter prediction result at 8 m/s
4 基于气动力数据驱动模型的失速颤振分岔速度预测与结果分析
来流速度是影响失速颤振特性的重要因素之一,翼型动态失速气动力特性随来流速度变化显著,因而需要对不同来流速度下的气动力系数进行学习,从而准确预测失速颤振分岔速度.在此对第2 节所建立的气动力数据驱动模型进行扩展,将来流速度U扩展为迎角序列矢量 α 的第2 分量,如下式所示,分别输入RNN 与branch net,trunk net 则与上一节中相同
同样地,采用文献[24]中包含不同来流速度的训练信号进行训练.其中的来流速度为U=(6,7,8,9)m/s,呈阶梯状递增.除输入向量维度外,神经网络的其他结构保持不变.训练过程如图11 所示,待误差稳定并小于10%后完成训练.

图11 有速度输入的训练过程Fig.11 Training process with velocity input
同样地,采用正弦信号对训练后的神经网络进行泛化测试.测试信号幅值为0.698 rad,减缩频率为0.202,在不同来流速度下进行泛化测试,其中包括了9.5 m/s 的外插工况,结果见表3 与图12.G-DeepONet与L-DeepONet 平均泛化误差均低于GRU 与LSTM.在 9 .5 m/s 的外插工况下,预测误差均显著上升,但深度算子神经网络组的预测误差仍低于RNN 组,体现出了更好的泛化能力.

表3 不同速度输入下的极限环振荡幅值泛化误差Table 3 Generalization error with different flow velocities

图12 失速颤振幅值随来流速度的变化Fig.12 Stall flutter amplitude versus velocity
选取L-DeepONet 进行失速颤振分岔速度预测,并与流固耦合结果进行对比,结果见图13.有速度输入时,所建立的数据驱动模型能够较好地预测失速颤振分岔现象,分岔速度为7.5 m/s,而流固耦合分岔速度在7~7.5 m/s 之间,取中值7.25 m/s,相对误差为3.45%.而无速度输入组则没有明显的分岔现象.

图13 不同速度输入下的泛化测试结果Fig.13 Generalization test results with different velocities
最后对流固耦合方法与数据驱动建模方法的预测时间进行对比.基于CFD 的流固耦合方法对图13中7 个来流速度进行计算的总耗时为8404 s,而两种L-DeepONet 预测时长均为7.5 s,具有更高的预测效率.
5 结论
本文提出了一种基于深度算子神经网络的翼型非定常气动力数据驱动建模方法,实现了基于深度算子神经网络气动力数据驱动模型的二维翼型失速颤振分析.
(1)在气动力预测方面,深度算子神经网络数据驱动模型与传统RNN 相比引入了主干网络,通过主干网络对RNN 的输出进行了不同时间步气动力的权重优化,更能体现非定常气动力的时滞特性,也具有更低的泛化误差,同时误差分散性大幅降低.
(2)在失速颤振极限环振荡幅值预测方面,在相同网络结构参数下,基于深度算子神经网络模型的幅值预测误差在2%以内,优于基于RNN 模型的预测结果.
(3)在失速颤振分岔速度预测方面,考虑速度输入的数据驱动模型预测精度显著高于没有速度输入的数据驱动模型.

