同阶元型为2 的幂的群
邹 玄,沈如林
(湖北民族学院 数学系,湖北 恩施445000)
在有限群里,同阶元集合的长度是很重要的,它的值等于同阶元共轭类长度的和.文献[1]It介绍了共轭型的概念,设G是一个有限群,{n1,n2,…,nr}为正整数集合,并且ni为G中的元的中心化子在G中的指数,这里不妨假设n1>n2>…>nr=1,则向量(n1,n2,…,nr)被称作为群的共轭型,显然只有Abel 群的共轭型为(1),文献[1-2]It证明了有限群中共轭型为(n1,1)和(n1,n2,1)的群是幂零群和可解群,后来文献[3]研究了有限单群中共轭型为(n1,n2,n3,1)的类型. 类似,在上面It给出共轭类型的概念里,还将共轭类长度替换同阶元长度,并且能得到一个类似的定义,即同阶元型.
定义1 设G是一个有限群,定义g~h,如果g,h∈G且有相同的阶,有这种关系的等价类的集合长度称作G的同阶元型.
文献[4]研究了同阶元型{1,15,20,24}的群,证明了此时这样的群只能是交错单群A5.文献[5]分类了同阶元型(n1,1)和(n1,n2,1)的群.最近文献[6]研究了某些单群用同阶元型刻画的问题. 记Zn为n阶循环群,并记;记为的素因子集合,并记π'为π 在素数集合中的补,G的子群H称为π-Hall 子群,若π(H)⊆π 且π(|G|/|H|)∩π =φ.在本文中将研究同阶元型为{1,2,22,…,2m}的群,证明下面的定理.
定理1 设G是群(不必有限),若G的同阶元型为{1,2,22,…,2m},其中m为有限数,则G同构于群Z2m+1×Zr1×Zr2×…×Zrt的某个子群,其中ri=2ei+1 为费马素数(ei≤m,1≤i≤t).
注意因为费马素数紧紧发现F0=3,F1=5,F2=17,F3=257,F4=65537,有人猜想不再存在其它的费马素数了.
1 一些引理
引理1[7](Frobenius)设G是有限群,n为的正整数因子,则n|f(n).
引理2 φ(n)|sn(其中sn表示G中n阶元的个数,φ(n)表示Euler 函数).
引理3 若G的Sylow 2-子群循环,则G存在正规2-补,即存在2'-Hall 正规子群.
证明 设P2为G的Sylow 2 子群且循环,则由N/C定理知:NG(P2)/CG(P2)<~Aut(P2)而循环群P2的自同构的阶为φ(|P2|),它仍为2 的幂,由Lagrange 定理知:|NG(P2)/CG(P2)|是φ(|P2|)的因子,且|NG(P2)/CG(P2)|为奇数,故NG(P2)=CG(P2),由Burnsidep-幂零准则知:存在2'-Hall 正规子群,即存在2'-Hall 正规子群.
引理4[4]设G是一个群,且G中的元素个数大于2,如果G中同阶元的最大阶为s,s为有限数,则G有限,并且|G|≤s(s2-1).
引理5 设G是有限群,若G的同阶元型为{1,2,22,…,2m},则的素因子为2 或费马素数.
证明 设p∈π(G),则p|1 +sp,而sp=2i(i=1,2,…,m).故p=2 或者为费马素数.
引理6 设G是有限群,同阶元型为{1,2,22,…,2m},若G为偶阶群,则Sylow 2-子群循环且正规.
证明 用数学归纳法证明s2i=2i-1,其中i≥0.显然2∈π(G),当i=1 时,成立. 若i时成立,考虑i+1的情形,因为s2i=2i-1,由Frobenius 定理知:
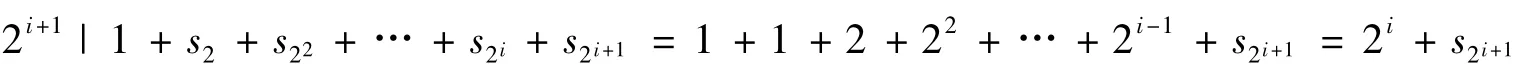
为了完成定理的证明,还需要一些关于素数的结论.把rm(a)叫做am-1 的本原素因子,如果rm(a)|am-1,但rm(a)不整除ai-1(i<m).显然,对本原素因子p=rm(a),则m|p-1 总是成立的. 设Φn(x)为第n个本原多项式,则xn-1 可以分解成若干本原多项式的乘积,其中本原多项式的个数为n的某个素因子,即xn-1 =∏d|nΦd(x).下面的引理说明了本原素因子的存在性,以及本原素因子与本原多项式的密切联系.
引理7 设qn-1 至少有一个本原素因子且n≥3,则Φn(q)=(P(n),Φn(q))·Φn(q)这里P(n)是n的最大素因子,Zn(q)是qn-1 包含所有本原素因子的最大素因子.
证明 由文献[9]中的207 页及文献[7]中的引理2.1 有:Zn(q)|Φn(q)以及Φn(q)|Zn(q)·P(n),从而Φn(q)=(P(n),Φn(q))·Zn(q).
引理8[9]设p是qk-1 的本原奇素因子,则p|Φf(q)当且仅当f=kpj,j≥0.
引理9[10](Schru-Zassenhaus) 设G为有限群,N为G的正规Hall 子群,则N在G中存在补子群,且任何两个补子群共轭.
2 定理1 的证明
根据引理4,不妨设G为有限群,而由引理3、引理5 和引理9 知:G≅Z2m1×K,其中m1≤m+1,设p∈π(K),由引理5 知:p为费马素数,设p=2e+1,(e≤m).由引理2 知:Sylowp-子群方次数为p,由引理1 有:p|1 +sp,即(1 +2e)l|1 +2i,(e≤i≤m),因为i≥e,由引理7 和引理8 有:l=1 且sp=2pt·x=2i,(t≥1),故G中的Sylowp-子群的个数为2pt·x-e.又因为G中的Sylow 子群的个数为K中的Sylow 子群的个数,故Sylowp-子群的个数为素数,即2pt·x-e=1,从而i=e,这样G中的Sylowp-子群P正规且|P| =p,故G同构于Z2m+1×Zr1×Zr2×…×Zrt的一个子群,这里ri为费马素数且ri-1≤2m,i=1,2,…,t.即证.
推论1 设G为群,G的同阶元型为某些2 的幂的集合,则G为幂零群.
本结果证明了当一个群G的同阶元型与循环2-群的同阶元型一致,G必为幂零群;当然可以类似的证明如果同阶元型里面的元为2 的幂,可能不是连续的幂,也可以得到同样的结果,比如同阶元型为{1,4},这样的群必然为Z5,Z10,但是否当G的同阶元型与循环群的同阶元型一致时,G仍为幂零群?
[4] Shen R,Shao C,Jiang Q,et al.A new characterization A5[J].Monatshefte Fur Mathematik,2010,160:337-341.
[5] Rulin Shen.On groups with given same-order types[J].Communicationin Algebra,2012,40:2140-2150.
[6] Shitian Liu.A characterization of Projectine Special Unitary groupU3(5)by use[J].Arab Jonrnal of Wathematical Sciences,2014,20(1):133-140.
[7] Feit W.On large Zsigmondy primes[J].Proc Amer Math Soc,1988,120:29-36.
[8] Malle G,Moreto A,Navarro G.Element orders and Sylow structure[J].Mathematische Zeitschrift,2006,252:223-230.
[9] Ribenboin P. The Book of Prime Number Records,Second Edition[M].New York:Springer-Verlag,1989.
[10] 徐明耀.有限群导引(上册)[M].北京:科学出版社,2006.

