加权p,q对称熵损失下Lomax分布形状参数的Bayes估计与性质

徐 宝,赵仲达,华志强

(1.吉林师范大学 数学与计算机学院,吉林 四平 136000;2.内蒙古民族大学 数学科学学院,内蒙古 通辽 028043)

0 引言

Lomax分布作为指数伽玛分布的混合分布由K.S.Lomax[1]而提出,也称为第二型Pareto分布,该分布的概率密度函数以及分布函数分别为:

(1)

其中λ为尺度参数,θ为形状参数.易知Lomax的期望为

方差为

1954年,K.S.Lomax[1]首次引进Lomax分布,由于Lomax分布在生物科学、分析医学和工程科学等实际生产生活中有着广泛的应用,因此该分布的统计推断理论被许多统计学者密切关注.损失函数形式的选取在研究统计决策问题的过程中起着非常重要的作用,在很大程度上决定了统计决策以及参数估计的优劣性.姚惠[2]研究了在Linex损失下Lomax分布形状参数的Bayes估计;周明元[3]研究了在对称熵损失函数下两参数 Lomax分布形状参数的Bayes估计;葛露娟等[4]研究了在Mlinex损失函数下Lomax分布的几种Bayes估计.

本文所考虑的加权p,q对称熵损失函数[5]为

(2)

其中δ为待估参数θ的估计量,可以看出交换二者以及p,q的位置,不影响此损失函数的形式.当p=q时损失函数(2)具有与绝对损失和平方损失一样的对称性[6].

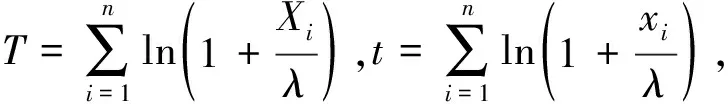
下面将基于此损失函数来研究Lomax分布形状参数的Bayes估计及其性质.

1 加权p,q对称熵损失函数下Lomax分布形状参数θ的Bayes估计

在Bayes框架下,基于损失函数(2)来研究Lomax分布形状参数θ的Bayes估计的形式及其性质.首先推导出任意先验分布下参数θ的Bayes估计.

定理1设X=(X1,X2,…,Xn)是来自Lomax总体(1)的一个简单随机样本,假设尺度参数λ已知的,在加权p,q对称熵损失函数(2)下,对任意先验分布,形状参数θ的Bayes估计为

证明设π(θ|x)为后验密度,则决策函数δ的后验风险为

由于后验风险最小的决策函数是贝叶斯风险,用微积分求极小值点的方法,对后验风险R(δ|x)关于δ求导得

解方程得

由于

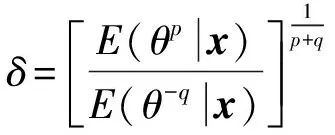
下面选取参数θ的无信息先验分布即广义先验分布π(θ)=1来讨论参数θ的Bayes估计的精确形式.

定理2设X=(X1,X2,…,Xn)是来自Lomax总体(1)的一个简单随机样本,设尺度参数λ已知,形状参数θ的先验分布为广义先验分布π(θ)=1,则在加权p,q对称熵损失函数(2)下,参数θ的Bayes估计为

证明此时参数θ的后验密度函数为

由定理1可知在损失函数(2)下,形状参数θ基于任意先验分布的Bayes估计为

而

同理可以得到

则

下面考虑当先验分布为Gamma分布时参数θ的Bayes估计的精确形式.

定理3设X=(X1,X2,…,Xn)是来自Lomax总体(1)的一个简单随机样本,设尺度参数λ是已知的,形状参数θ的先验分布为Gamma分布Γ(a,b),a>0,b>0,则在加权p,q对称熵损失函数(2)下,参数θ唯一的Bayes估计为

证明参数θ的先验密度为π(θ)=Γ-1(a)baθa-1e-bθ,样本X=(X1,X2,…,Xn)的概率函数为f(x|θ)=λ-nθne-t(θ+1),后验密度为

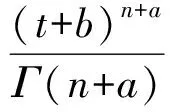
则

同理可得

故在加权p,q对称熵损失函数(2)下,参数θ有唯一的Bayes估计为

下面讨论参数θ的Bayes估计的性质.行文需要,列出如下引理.

引理1[7]设统计判决问题的损失函数为L(θ,δ),参数θ的先验分布为π(θ),G为非随机化决策函数X～f(x;θ),θ∈Θ,若损失函数L(θ,δ)为G上的严格凸函数,则该统计判决问题的贝叶斯解几乎处处唯一.

引理2[8]在给定的贝叶斯决策问题中,若在给定先验分布π(θ)下,参数的贝叶斯估计是唯一的,则它是可容许的.

定理4在加权p,q对称熵损失函数(2)下,Lomax分布形状参数θ的Bayes估计是可容许的.

证明在定理1中已经证明了对于δ求二阶偏导结果大于零,即Lomax分布参数的Bayes估计是关于δ的严格凸函数,根据引理1推得该贝叶斯估计具有唯一性.最后由引理2得到Lomax分布参数θ在加权p,q对称熵损失函数(2)下基于Γ(a,b)先验分布的Bayes估计是容许性的.

2 加权p,q对称熵损失下Lomax分布形状参数θ的多层Bayes估计

在Bayes统计推断中,经常会遇到含有超参数的先验分布,当不能确定先验分布中的超参数时,可以对超参数再给出一个先验,第二个先验称为超先验,由先验和超先验决定的一个新先验称为多层先验.

上一节所选取的形状参数θ的共轭先验分布Γ(a,b)中含有超参数a和b,本节对参数a和b再给一个先验分布,进而讨论参数在多层先验分布下的Bayes估计即多层Bayes估计.根据文献[9]考虑Bayes估计的稳健性最终确定00,c是常数).取超参数a和b的先验分布分别为均匀分布U(0,1)和U(0,c)上,其密度函数分别为

(3)

定理5若Lomax分布形状参数的先验分布为Γ(a,b),超参数的a和b先验分布为(3),则在加权p,q对称熵损失函数(2)下,参数的多层Bayes估计为

证明前面给出了超参数a和b的先验分布分别为π(a)和π(b),假设a和b独立,参数θ的多层先验密度为

进而得到参数θ的后验密度为

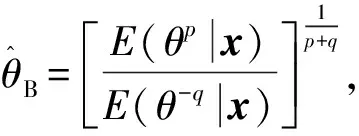
同理得到E(θ-q|x)的精确表达式为

最终得到参数θ的多层Bayes估计的精确表达式为

3 加权p,q对称熵损失下Lomax分布形状参数θ的E-Bayes估计

从上一节的讨论中可以看出多层Bayes估计的应用较为复杂,其结果需要通过大量的积分计算才能得到.E-Bayes估计的出现解决了此问题,下面将结合定义来研究Lomax分布形状参数θ的E-Bayes估计.

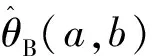
从定义中可以看出参数θ的E-Bayes估计

是θ的Bayes估计对超参数a和b的数学期望.

定理6若Lomax分布形状参数θ的先验分布为Γ(a,b),则在加权p,q对称熵损失函数下参数θ的E-Bayes估计为

其中超参数a,b的先验分布为π(a)=U(0,1),π(b)=U(0,c).

证明由定理1知,参数θ在损失函数(2)下的Bayes估计为

则

从定理5和定理6中可以明显看出参数θ的E-Bayes估计的表达式比多层Bayes估计简单,解决了估计方法的易算性,是对多层Bayes估计的修正.

5 数值模拟

为验证本文所研究内容的准确性,下面运用MATLAB进行随机模拟计算,通过比较在不同情况下所模拟计算出估计的均值、均方误差以及偏差绝对值的变化情况,从而验证估计的准确性与所使用的方法的合理性.

设定Gamma分布中参数a=1,b=1;加权p,q对称熵损失函数(2)中的p=1,q=1;令尺度参数λ=1;形状参数θ=1,5,10;分别计算当样本容量n为5,25,50,75,100时参数θ在加权p,q对称熵损失函数(2)下的Bayes估计;重复模拟1 000次,并计算出参数θ的Bayes估计的均值、均方误差以及估计的偏差绝对值,分别用GB、MSE、Abs表示.随机模拟结果见表1—3.

表1 加权p,q对称熵损失函数下参数的Bayes估计的模拟结果(θ=1)

表2 加权p,q对称熵损失函数下参数的Bayes估计的模拟结果(θ=5)

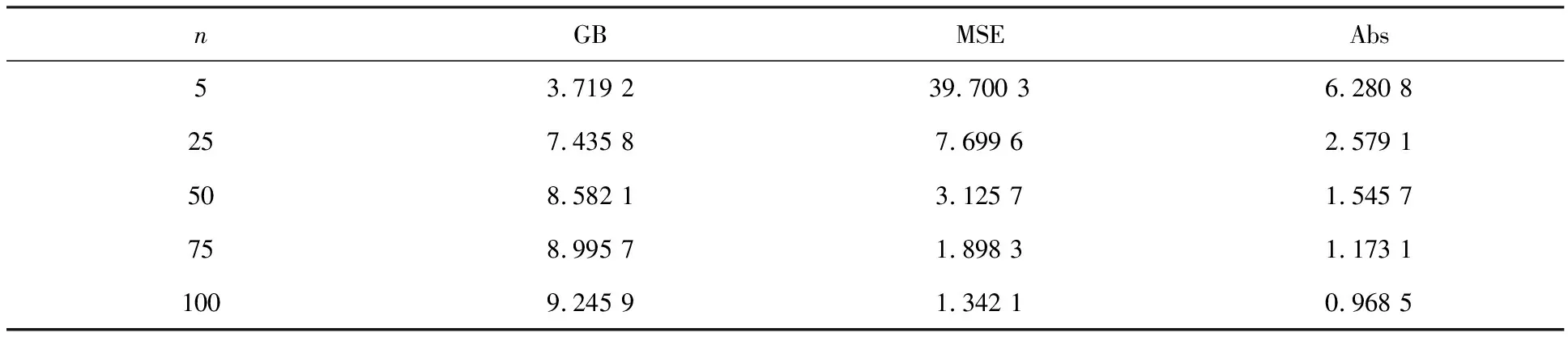
表3 加权p,q对称熵损失函数下参数的Bayes估计的模拟结果(θ=10)

由表1—3的模拟结果可以看出:无论参数θ取何值时,随着样本容量的增大,在加权p,q对称熵损失函数(2)下,参数的Bayes估计的均方误差和偏差绝对值都在减小,估计值逐渐递增地接近真值.从表中还可以看出当参数θ取值较大时,选取较小容量的样本空间所产生的估计结果误差较大,因此,当参数值较大时,选取较大的样本容量才能使估计的效果最好.

下面对参数θ的E-Bayes估计进行随机模拟.设定Gamma分布中超参数a,b的先验分布为π(a)=U(0,1),π(b)=U(0,c);令c=1,加权p,q对称熵损失函数(2)中的p=1,q=1;令尺度参数λ=1;形状参数θ=1,5;分别计算当样本容量n为5,25,50,75,100时参数θ在加权p,q对称熵损失函数(2)下的E-Bayes估计;重复模拟1 000次,并计算出参数θ的E-Bayes估计的均值、均方误差以及估计的偏差绝对值,分别用EB、MSE、Abs表示.随机模拟结果见表4—5.

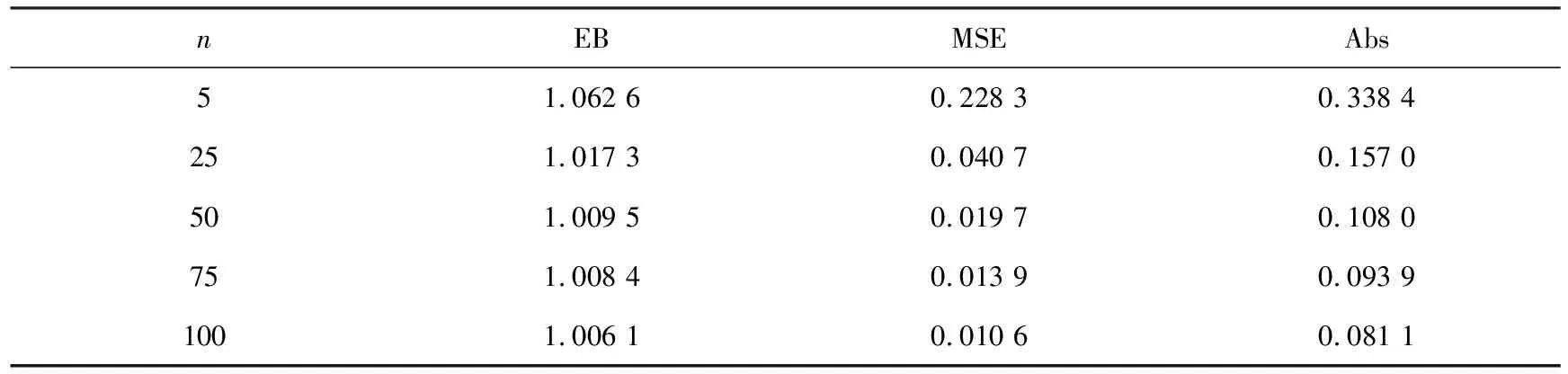
表4 加权p,q对称熵损失函数(2)下参数的E-Bayes估计的模拟结果(θ=1)

从表4—5的模拟结果可以看出:选取较大的样本容量能使估计效果更好,无论参数取1或5,随着样本容量的增大,其E-Bayes估计值都逐渐递增地接近估计的真值,其均方误差和偏差绝对值也逐渐减小.因此,在下面模拟实验中令样本容量n=100固定不变,研究c值的变化对随机模拟结果所产生的影响,为考虑估计结果的稳健性,令c=0.1,0.3,0.5,0.7,0.9.模拟结果见表6—7.

从表6—7的模拟结果可以看出:当固定样本容量n=100不变,改变c时,形状参数θ的E-Bayes估计的均方误差和偏差绝对值相比表4和表5的模拟结果都比较小,并且精度较高,因此,在对Lomax分布下形状参数θ的深入研究与探索中可选用此方法.

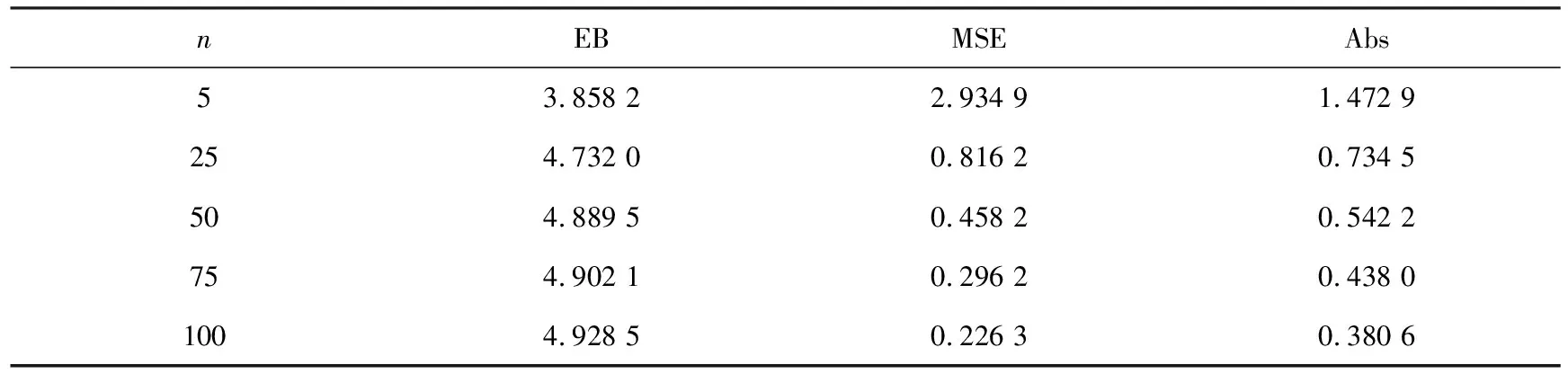
表5 加权p,q对称熵损失函数(2)下参数的E-Bayes估计的模拟结果(θ=5)

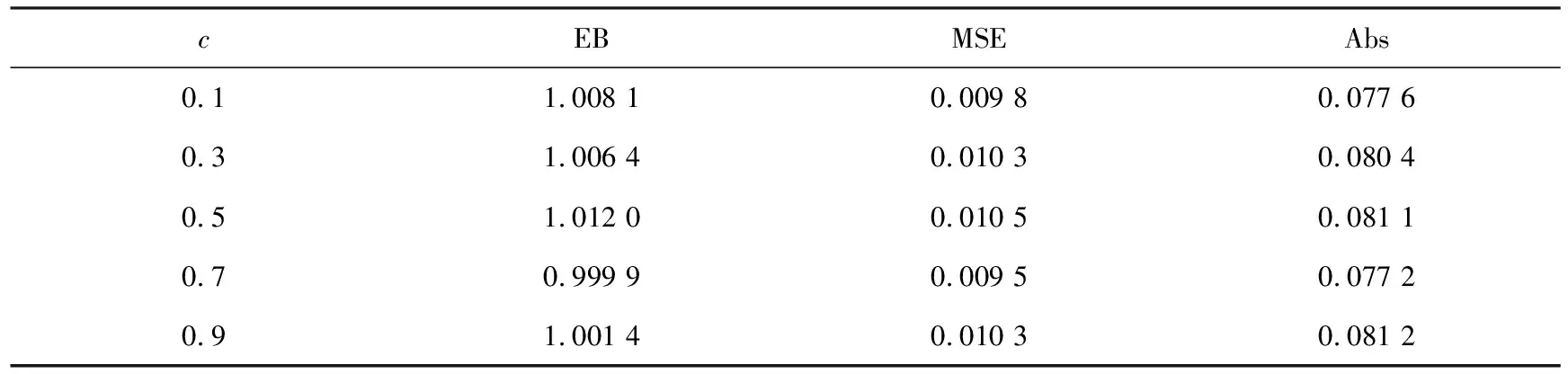
表6 加权p,q对称熵损失函数(2)下参数的E-Bayes估计的模拟结果(θ=1)

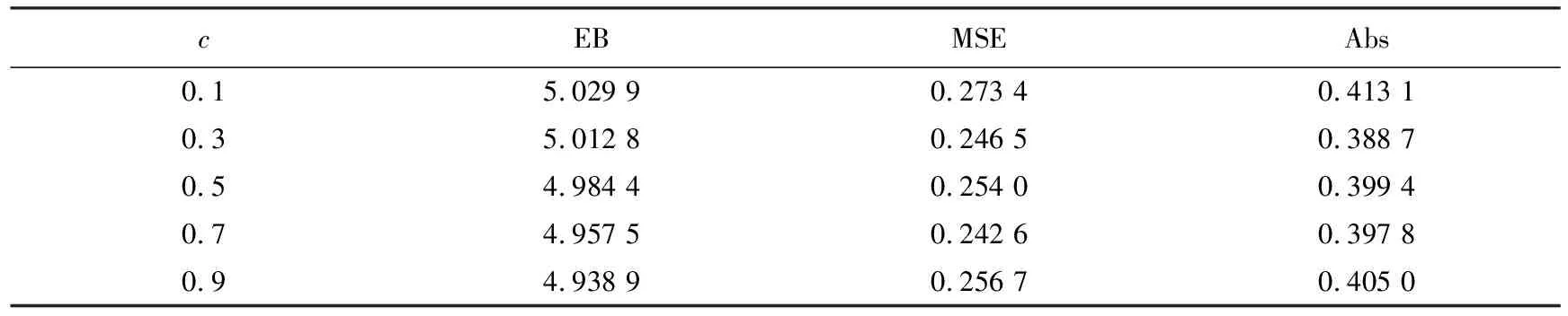
表7 加权p,q对称熵损失函数(2)下参数的E-Bayes估计的模拟结果(θ=5)

6 结语

本文基于加权p,q对称熵损失函数,当尺度参数λ已知时,讨论了两参数Lomax分布的形状参数θ在不同先验分布下的Bayes估计.同时讨论了在加权p,q对称熵损失函数下Lomax分布形状参数θ的多层Bayes估计以及E-Bayes估计.最后,对所得到的结论运用MATLAB进行随机模拟研究,验证了本文所使用方法以及结论的合理性.