一类带有奇异项和对数非局部源的抛物方程解的性质
吴秀兰,杨晓新
(长春理工大学 数学与统计学院,吉林 长春 130000)
0 引言
本文主要研究如下带有奇异项的一类非局部抛物方程:
(1)
其中:0 近年来,具有非局部源的抛物方程在不同的领域中被广泛地应用,取得了丰富的研究成果[1-6].2018年,冯敏和周军[7]研究了一类非局部源的抛物方程: (2) 给出了方程解的全局存在性及解在有限时刻爆破的性质.当k(t)=1时,文献[8-11]利用修正的位势井方法研究了一类具有奇异项的抛物方程问题: (3) 给出了弱解的全局存在性及爆破性.问题(3)中当k(t)≠1时,韩玉柱[12]给出了方程弱解在有限时间内爆破的性质.此外给出了爆破时间的上界和下界估计. 当问题(1)中的s=0时,L.J.Yan等[13]研究了非局部源抛物型方程 (4) 利用对Sobolev不等式和能量估计,在适当的条件下给出了解的爆破结果. 对于具有奇异项和对数非局部源的抛物型方程解的性质的研究较少.本文受问题(4)启发,研究了问题(1)解的性质,值得提出的是具有奇异项的对数非局部源抛物型方程弱解的性质研究目前还没有任何结果,这是本文的主要研究内容,由于奇异项的存在,具有对数非局部源的抛物型方程的经典方法不再适用,例如上下解,比较原理等.受文献[14-23]启发,利用截断函数,位势井法、函数逼近思想和对数Sobolev不等式等,证明了弱解的局部存在性,弱解的全局存在性和衰退估计,此外还给出了爆破结果. (5) (6) (7) 接下来给出几个引理. 引理1设μ是一个正数,则有下列不等式成立: splns≤(eμ)-1sp+μ,s≥1, |splns|≤(ep)-1,0 引理2[15]假设Ω是N中的有界光滑区域,则对任意和任意a>0,有 其中HN=H(N,Ω). 引理5[25]设f:+→+是一个非增函数,σ是一个非负常数,使得下述不等式成立: 则 (ⅰ) 当σ=0时,对于任意t≥0,有f(t)≤f(0)e1-ωt; (ⅲ) 在λ∈(0,λ*)上J(λu)递增,在λ∈(λ*,+∞)上J(λu)递减,且λ=λ*处J(λu)取得最大值; (ⅳ) 在λ∈(0,λ*)上I(λu)>0,在λ∈(λ*,+∞)上I(λu)<0且I(λ*u)=0. 下面给出问题(1)的弱解定义. (8) 证明证明分为三个步骤: 步骤1弱解的存在性 由引理7知un∈L∞(0,T;H),且满足 (9) 在式(9)中取φ=un,有 (10) 对式(10)右端进行估计,设Ω1={x∈Ω:|un|>1},Ω2={x∈Ω:|un|≤1},结合引理1、引理4、Young不等式和Sobolev不等式有 (11) 另一方面经过计算有 (12) 其中|x|≤L.结合式(10)—(12)可得 (13) 其中C1=(eμ)-1CGC(ε)(min{Ls,L-s,n-1})α. (14) 在问题(1)两端同时乘unt,在Ω×(0,t)上积分并结合式(5)有 (15) J(un0)≤C,∀n∈+. (16) 另一方面结合式(1)和式(11)可知 (17) 由式(15)—(17)可得 (18) 其中C(T,ε)是只依赖于T,ε的正常数. 由式(18)可得估计 (19) (20) 类似式(12)可得 (21) (22) (23) 结合估计式(19)、式(21)和Aubin-lions紧致性定理可知,存在函数u,使得当n→∞时有 un→u,在C(0,T;L2(Ω)) 中强收敛. (24) 所以根据式(24),当n→∞时有un(x,0)→u(x,0),a.e.于Ω.由注意1及极限的唯一性得u(x,0)=u0.式(24)蕴含了unln|un|→uln|u|,a.e.(x,t)∈Ω×(0,T).另一方面经直接计算并结合引理1及式(18)得 (25) unln|un|→uln|u|在L∞(0,T;L2(Ω)) 中弱*收敛. (26) 结合Hölder不等式有估计 这意味着 借助式(22)、式(23)、式(26),在式(9)中令n→+∞,有 则易知u是问题(1)在Ω×[0,T) 上的一个弱解. 步骤2能量等式 在问题(1)两端同时乘ut,在Ω×(0,t)上积分并结合式(5)有 (27) 步骤3唯一性 (28) 下面取 作为检验函数,结合式(28)有 其中M(u)=uln|u|在+→+上Lipschitz连续,结合Gronwall’s不等式得到解的唯一性. 证明证明分为两种情形: (29) J(u(t0))=d, (30) 或者 I(u(t0))=0. (31) 借助上述不等式,将式(5)和式(29)结合有 注意到上述不等式的右端常数不依赖于T,故对任意T>0,可取Tmax=T=+∞.借助上述不等式可知问题(1)在Ω×(0,∞)上有一个整体弱解u(x,t). (32) 结合问题(1)的第一个等式、式(5)和引理3有 (33) 结合式(32)—(33),可得 令上述不等式中的T→∞,利用引理5,得到衰减估计 (34) J(u(t1))=d, (35) 或者 I(u(t1))=0. (36) 由引理6(ⅳ)和I(u(t))<0,存在一个λ*<1使得I(λ*u)=0.那么有 (37) (38) (39) (40) 接下来结合引理1与式(6)得到 (41) 另一方面结合式(38)可以发现存在t1∈(0,t),使得 (42) 其中|x| 对上述不等式运用Gronwall’s不等式可以得出 ln(L(t)) 即 (43) 本文研究了一类具有奇异项和对数非局部源的抛物方程的初边值问题.利用截断函数和极限逼近思想得到问题弱解的局部存在性;利用修正位势井及对数Sobolev不等式和Hardy-Sobolev不等式给出了问题弱解的整体存在性及衰退估计,并在适当的条件下得到了问题弱解在无穷远处爆破.1 准备工作
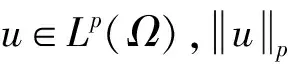
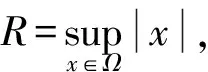
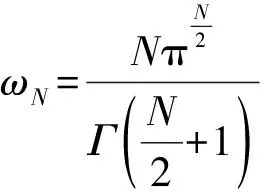
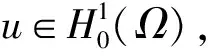
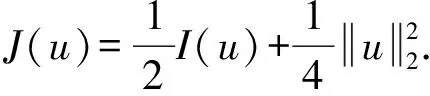
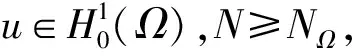
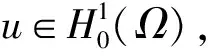
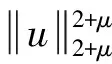
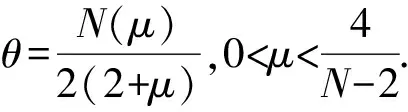
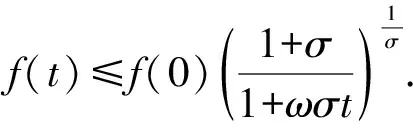
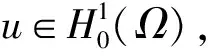
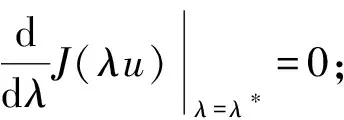
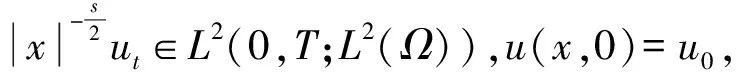
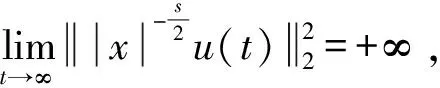
2 局部存在性
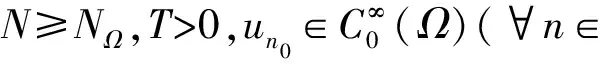
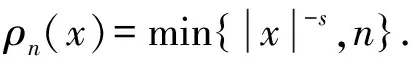
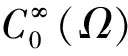
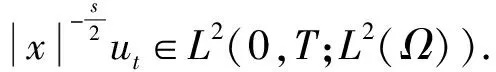
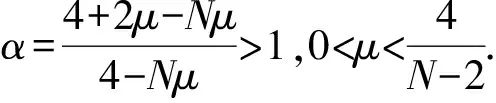
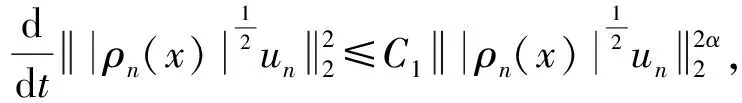
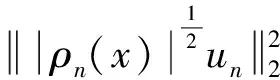
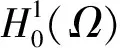
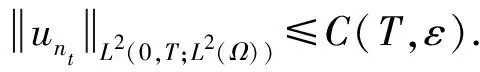
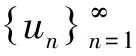
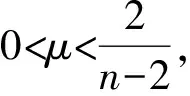
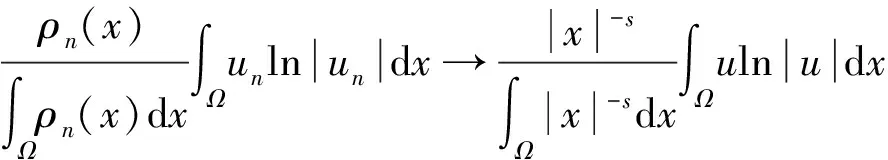

3 整体存在性和衰减估计
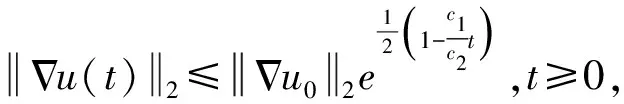
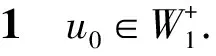
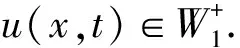
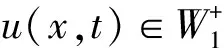
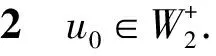
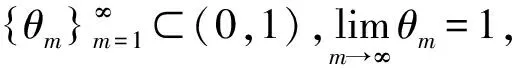
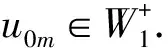
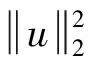
4 无穷远处爆破结果
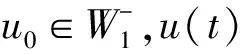
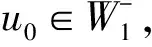

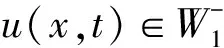

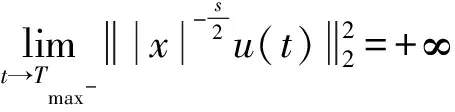
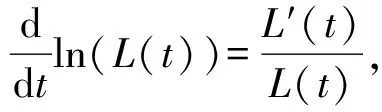
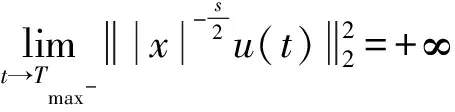
5 结语

