基于改进的距离函数法的多响应稳健参数设计

何 桢，王 晶,2 ， 李湧 范

(1. 天津大学管理学院，天津 300072；2. 南开大学泰达学院，天津 300457；3. 中国质量认证中心，北京 100070)

响应曲面方法(response surface methodology，RSM)最早由Box和Wilson提出，由于其设计思想先于田口稳健性设计方法，所以大多数 RSM 都没有考虑稳健参数设计问题．Vining和 Myers[1]提出了一种将响应曲面方法与稳健性思想结合起来的双响应方法，通过对一个质量特性的均值和方差进行拟合，根据拟合的响应曲面模型来优化均值并减少方差，从而得到稳健的过程参数．然而，该方法主要解决的是单响应稳健参数设计问题．在现实生产过程中，经常会遇到多响应参数设计问题，如手机、半导体、锂电池生产、冶金、化工等产品设计和过程设计中，往往存在多个质量特性值．多响应问题通常不存在一组特定的输入变量，可使所有响应变量同时达到最优．解决多响应问题的一个简单有效的方法就是重叠等值线图法，该方法在一个图形中为多个响应绘制等值线图，然后通过观察找出最优解．但这种方法通常只适于输入变量和响应变量很少的情况．另一类解决多响应问题的思路是运用数学的方法将多个响应转化为单个响应，然后再进行优化，如满意度函数法、多元损失函数法和广义距离函数法等．Derringer与Suich[2]提出的满意度函数法由于未考虑响应之间的相关性，该方法难以应对在诸如化工、电子等行业中经常遇到的多响应相关的情况．Pignatiello[3]、Vining[4]和Ko等[5]提出的质量损失函数法虽然考虑了过程的经济性，但是其成本矩阵的确定过多依赖于定性分析．广义距离函数法是由Khuri和Conlon等[6]提出的，使用的是能够消除方差和交互作用负面影响的马氏距离，因此也称为马氏距离函数法．该方法使用响应间的方差-协方差矩阵，考虑了响应间的相关性，是一种应用广泛的多响应优化方法，但仍未考虑产品或过程的稳健性问题．近年来，虽有很多学者对该问题进行研究[7-8]，但是，有关如何充分利用 RSM 的响应曲面信息，对多响应稳健性参数设计进行的研究还非常有限[9]．

如何解决多响应问题中的稳健参数设计问题，是当今国内外质量工程领域研究的热点问题．多响应稳健参数设计方法发展至今，大多忽略了可控因子的波动对响应的影响．然而在实际生产过程中，可控因子也存在一定变异，当可控因子发生微小变动时，若响应输出值的变动较大，则认为该产品或过程不稳健．笔者针对目前研究中存在的不足，考虑响应对可控因子波动的稳健性，对广义距离函数进行了改进，考虑了多响应问题的最优性及稳健性，提出了稳健优化总体广义距离函数方法，并用该方法对文献[10]中的实例进行了应用验证．

1 最优点及稳健点的确定

试验区域中各个响应的最优值通常利用Derringer与Suich[2]的满意度函数法通过对各个响应单独优化求得．令 Ti表示目标值，Li表示规格下限，Ui表示规格上限，则对于望大特性的响应变量 yi，其满意度函数为

对于望小特性的响应变量yi，其满意度函数为

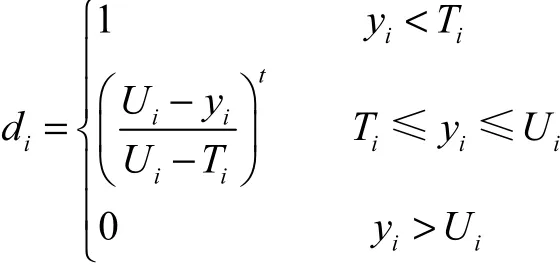
对于望目特性的响应变量yi，其满意度函数为

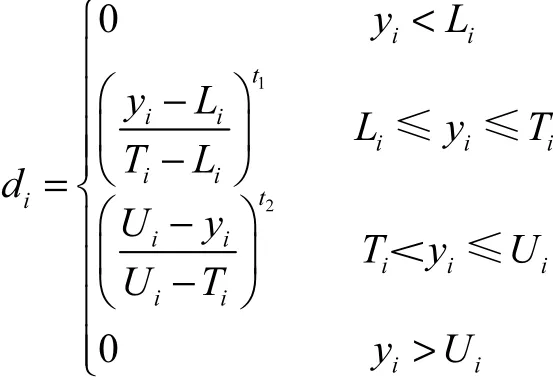
通过最大化各个响应的满意度函数，可以分别得到各响应的最优点和最优值．

在多响应稳健参数设计中，结果的最优性和稳健性同等重要．本文利用稳健满意度函数法[11]寻找试验区域中的稳健点．对于试验区域中的任意一点，以该点为中心定义一个半径为 r的圆形区域，用以描述该点处可控因子的波动范围．在此区域中可分别计算各响应的极差

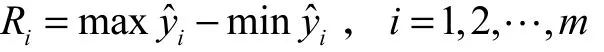
则对于响应变量yi，其稳健满意度函数为

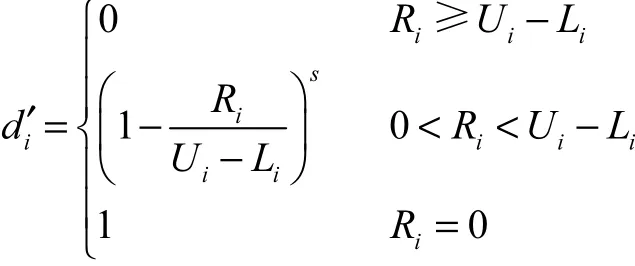
对于各个响应变量，使其稳健满意度函数最大的点可认为是试验区域中该响应变量的稳健点．在各响应的稳健点处，响应受可控因子波动的影响最小．

2 改进的稳健优化总体广义距离函数方法

传统的广义距离函数法使用广义距离来衡量各响应与其最优值之间的偏差，用响应的方差-协方差结构来估计各响应距其最优值距离的权重，将多响应优化问题转化为使广义距离最小化问题，来确定最佳的操作条件．但是，该方法仅考虑了响应的最优性问题．考虑到可控因子的波动对响应稳健性的影响，利用稳健满意度函数法计算出各响应的稳健解，定义一个稳健广义距离函数来衡量各个响应与其稳健值之间的偏差，然后使其最小化，从而使得多个响应同时达到或接近其稳健值，考虑了响应的稳健性要求．然而从统计分析及质量管理的角度出发，响应的最优性以及稳健性同等重要．稳健优化总体广义距离函数法通过对优化广义距离和稳健广义距离进行权衡，求二者的几何均值，然后使其最小化，得到稳健最优的操作条件，使优化的响应对可控因子的波动具有稳健性．

假设某一生产过程中所有m个响应都依赖于同一组 k个输入变量{x1，x2，…，xk}，共计 n次试验，且均可以用同阶次的多项式回归模型表示．则第i个响应的二阶模型可以用向量形式表示为

式中：yi为一个n×1响应矩阵，表示第i个响应的n个观测值；X为n×p设计矩阵，p =(k + 1)(k +2)/2；βi为表示回归系数的p×1列向量；εi为一个n×1列向量，表示第 i个响应的随机误差，服从均值为 0、方差为σii的正态分布．进一步假设第i个响应的随机误差与第 j个响应的随机误差的协方差cov(εi,εj)=σijIn，i ≠ j = 1,2,… ,m，其中In为n×n单位矩阵．βi的最小二乘估计值可推导为=(X ′X )−1，则第 i个响应的二阶拟合模型为

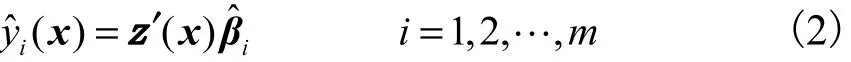
var[yˆ(x ) ] = z ′(x ) (X ′X )−1z ( x)σ i = 1,2,…,m

i ii yˆi(x)和yˆj(x)的协方差为

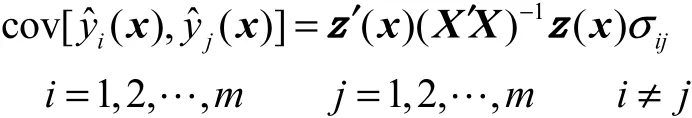
其中ijσ为方差-协方差矩阵Σ的第(i，j)个元素．Σ的无偏估计可表示为

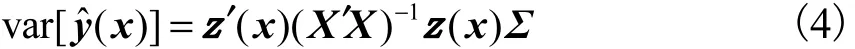
用ˆΣ替代式(4)中的Σ可以得到ˆ var[()]yx 的无偏估计值

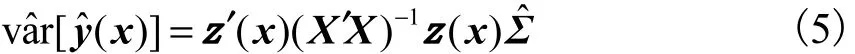
用 θi表示响应yi在试验区域内单独优化时得到的最优值，θ ＝ [θ1,θ2,… ,θm]′ 表示由这些最优值构造的m×1向量，则衡量各个响应与其最优值之间偏差的优化广义距离函数为

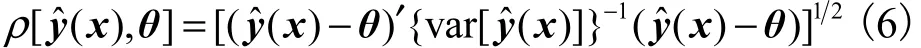
因为式(6)中 v ar[yˆ(x ) ]是正定矩阵，故而 { var[yˆ(x)]}−1也是正定矩阵，因此当yˆ(x)≠ θ 时，距离ρ[yˆ(x),θ]严格为正．将响应的方差-协方差矩阵的估计形式(5)代入式(6)中，可得

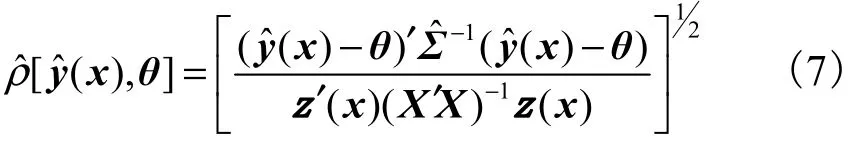
通过最小化广义距离 ρˆ[yˆ(x),θ]可确定最佳的操作条件，使各响应同时达到或接近最优值．

用φi表示响应yi在试验区域内得到的各自稳健点的响应值，φ ＝ [φ1,φ2,… ,φm]′ 表示由这些稳健值构造的 m×1向量，则衡量各个响应与其稳健值之间偏差的稳健广义距离函数为

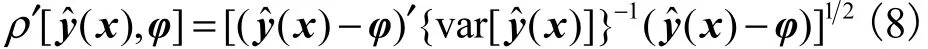
将式(5)代入上式，可得其估计值为

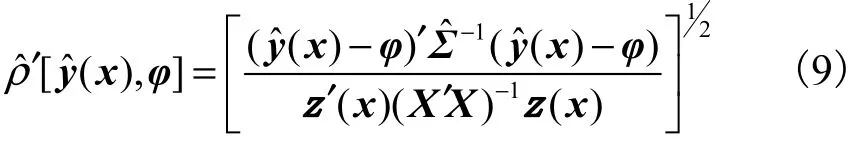
通过最小化 ρˆ′[yˆ(x),φ]可确定最稳健的操作条件．

考虑多响应的最优性和稳健性的权衡问题，稳健优化总体广义距离表达式为

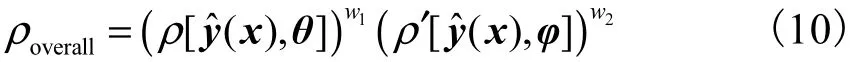
式中 w1和 w2分别为优化广义距离和稳健广义距离的权重，均为正实数且满足 w1+ w2= 1．使稳健优化总体广义距离最小的解可认为是过程的稳健优化解．根据多响应问题的最优性及稳健性的重要程度，权重w1和w2可选择不同的取值．当w1＝1、w2=0时，ρoverall=ρ[yˆ(x),θ]，只考虑多响应的最优性问题；当w1＝0、w2=1 时，ρoverall= ρ ′[yˆ(x),φ]，只考虑多响应的稳健性问题；当响应的最优性及稳健性具有相同的权重，即 w1＝w2=0.5时，ρoverall= ( ρ [ yˆ (x ) ,θ ] )12(ρ′[yˆ(x ),φ] )12，在实际生产中这种情况应用最为广泛．

3 实例分析

本文以 Myers与 Montgomery[10]介绍过的一个经典的多响应试验设计问题为例，利用本文提出的改进的稳健优化总体广义距离函数方法对其进行计算，并与传统方法进行比较分析．该试验通过调整一个化学过程的反应时间(x1)和反应温度(x2)，从而使其产量(y1)最大化，黏性(y2)达到目标值 65，同时使相对分子质量(y3)最小化，假定各响应变量可接受的范围分别是 y1≥78.5，62≤y2≤68，y3≤3,300．该试验是一个含有 5个中心点的中心复合设计，试验数据见表 1．

首先分别拟合出各响应的二阶响应曲面模型为

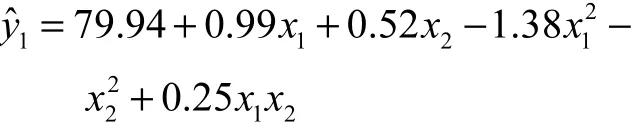
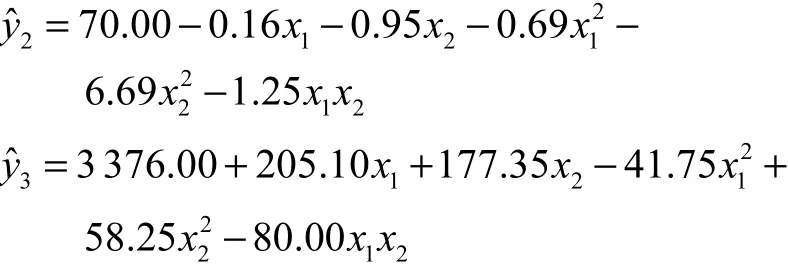
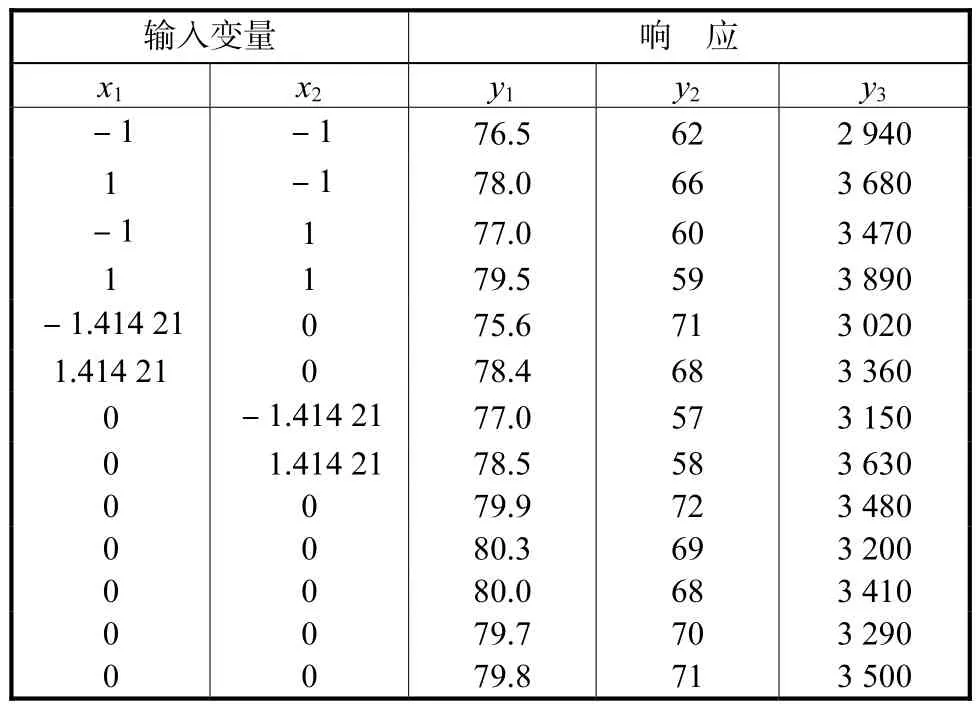
表1 试验数据Tab.1 Test data

方差-协方差矩阵的无偏估计值可通过式(3)计算得到，即

因为该试验设计是一个球形中心复合设计，因此试验区域是一个以原点为圆心、半径为 2的圆，根据拟合得到的二阶响应曲面模型，对各响应单独优化得到的最优值θi以及取得最优值的可控因子的参数组合如表 2所示．各响应在试验区域内得到的稳健值iφ及其对应的稳健点坐标见表3．

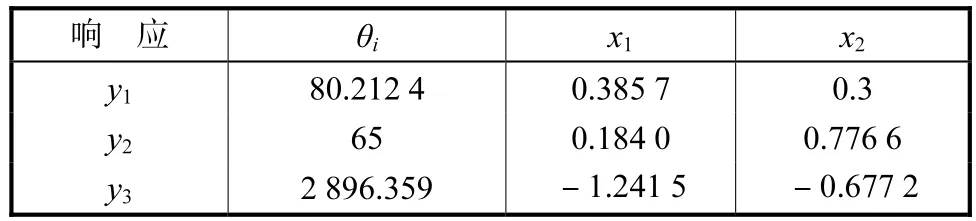
表2 各响应的最优值θi与其对应点坐标Tab.2 Optimal value θi and its corresponding location for each response

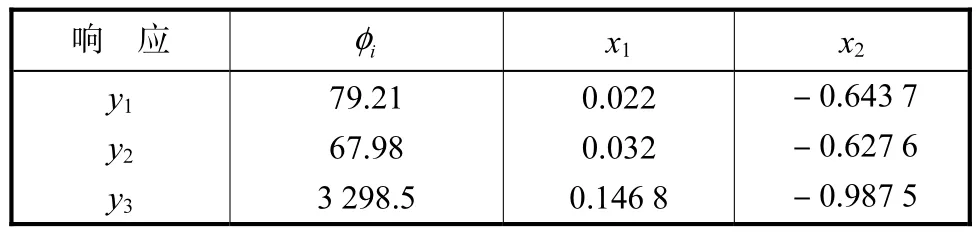
表3 各响应的稳健值iφ及其对应点坐标Tab.3 Robust value iφ and its corresponding location for each response

首先利用Minitab软件中多响应优化的满意度函数方法解决该问题．选择T1＝80作为响应产量y1的目标值，L1=78.5作为规格下限，为望大特性．令 T2＝65作为响应黏性 y2的目标值，L2=62作为规格下限，U2＝68作为规格上限，为望目特性．选择响应相对分子质量y3的目标值T3=3.100，规格上限为U3＝3.300，为望小特性．各响应单独满意度函数中所有权重均取 1．若考虑对3个响应同时优化，Minitab给出一组可控变量的最佳参数组合：x1=-0.157.1，x2=-0.785,7．在该水平下，产量的预测值为78.76，黏性的预测值为 66.47，相对分子质量的预测值为3.229.5．但是满意度函数法没有考虑最优点处是否稳健．在求得的最优点(－0.157.1，－0.785.7)处，定义可控因子的变动幅度为 0.01，则在此范围内各响应的极差分别为：R1＝0.065.1，R2＝0.215.2，R3＝7.526.2．

然后利用广义距离函数法对该问题进行分析．前面已经求得方差-协方差矩阵的无偏估计值和各响应单独优化时得到的最优值θi．利用广义距离函数法求得一组可控因子的最优参数组合：x1＝0.048,2，x2=-0.626,2．在该水平下，产量的预测值为79.26，黏性的预测值为 68，相对分子质量的预测值为3,300．同样，若考虑响应的稳健性，在求得的最优点(0.048,2，-0.626,2)处，定义可控因子的变动幅度为0.01，在该区域内各个响应的极差分别为：R1＝0.049,7，R2＝0.158,5，R3＝7.034,3．与满意度函数法相比，利用广义距离函数法计算得到的最优点处各响应的极差均较小，因此可以认为各响应在(0.048,2，-0.626,2)处，较之在(-0.157,1，-0.785,7)处更稳健．

在实际生产过程中，找到既稳健又可使响应达到最优的参数组合十分重要．下面利用本文提出的稳健优化总体广义距离函数法求解．当 w1=1、w2＝0时，得到的结果与利用传统广义距离函数法的结果相同．当 w1＝0、w2＝1时，求得的可控因子的稳健参数组合为 x1＝0.058,3，x2＝-0.641,6．在该水平下，产量的预测值为 79.24，黏性的预测值为 67.89，相对分子质量的预测值为 3,301，各响应的极差值为 R1＝0.048,9，R2＝0.161,0，R3＝6.886,3．虽然在该参数组合下响应的极差值最小，但是由于相对分子质量的预测值超出其规格上限，因此是不可接受的．通常情况下，需要同时考虑响应的最优性和稳健性问题，因此赋予二者相同的权重 w1＝w2＝0.5，利用该方法求得一组可控因子的稳健最优参数组合：x1＝0.051,2，x2＝-0.649．在该水平下，产量的预测值为79.22，黏性的预测值为 67.83，相对分子质量的预测值为3,298.5．当可控因子的变动幅度为0.01时，各响应的极差值为 R1＝0.049,5，R2＝0.163,5，R3＝6.904,0．比较利用3种方法计算得到的结果，如表4所示．

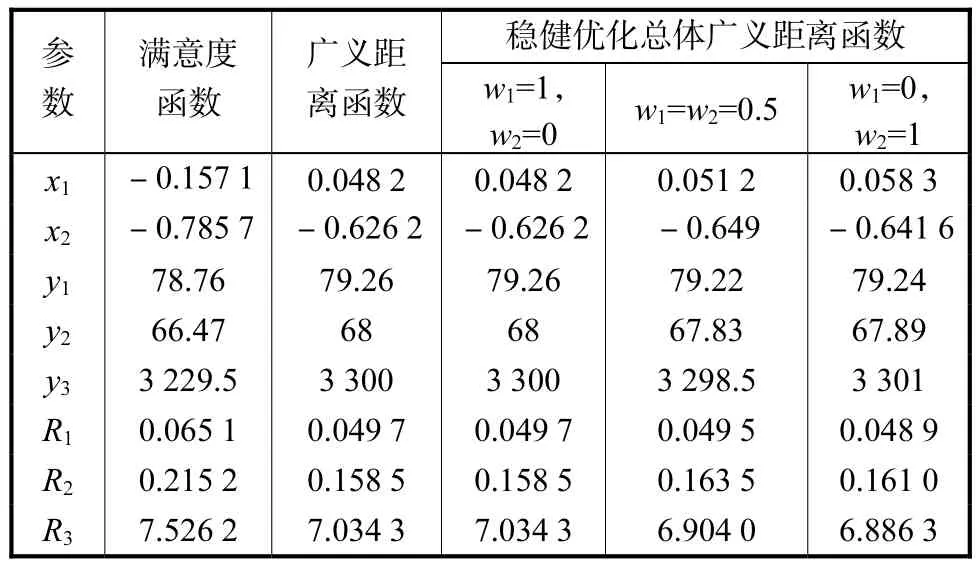
表4 改进的广义距离函数方法与传统方法的结果对比Tab.4 Comparison of results between improved generalized distance function method and traditional methods

若仅比较预测的响应值，3种方法中利用满意度函数法可以得到最好的结果，但是预测的响应极差较大，说明最优点处的稳健性较差．虽然另 2种方法得到的响应的预测值稍差，但是响应的稳健性都要好于满意度函数法计算的结果．另一方面，利用广义距离函数法预测的响应 y2和 y3都在响应的规格限上，可控因子的微小波动就可能会导致响应变量超出规格限，造成大量废品的产生．利用稳健优化广义距离函数进行分析：当 w1=1、w2=0时，可简化为传统广义距离函数法；当w1=w2=0.5时，预测的响应y1和y3的极差都要小于传统方法，表明点(0.051.2，－0.649)处的响应y1和y3更稳健．虽然响应y2的极差R2相对广义距离函数法更大，但是预测的响应值 67.83与广义距离函数法相比更接近目标值，不再是响应的规格限，可大大减少废品的产生．这说明利用改进的距离函数法对多响应问题进行优化时，权衡了响应的稳健性和最优性．随着稳健性的权重w2变大，预测的响应值的极差相应变小，但是同时响应值也逐渐远离目标值，当 w1=0、w2=1时，响应 y3的预测值 3,301已超出其规格限 3,300，不能满足顾客要求．因此在实际生产中通常选取 w1=w2=0.5，即式(10)取几何均值作为稳健优化广义距离函数．该方法与传统方法相比，考虑了响应的方差-协方差结构和可控因子的波动，使优化的响应对可控因子的波动具有稳健性．

4 结 语

多响应稳健参数设计是改进产品或过程质量的一个重要方法．本文基于广义距离函数法对多响应稳健参数设计进行了研究，考虑到响应的方差-协方差结构和可控因子的波动，提出了改进的稳健优化总体广义距离函数法，通过对优化广义距离和稳健广义距离进行权衡，将多响应稳健优化问题转化为使稳健优化总体广义距离最小化问题，从而得到稳健最优的操作条件，使优化的响应对可控因子的波动具有稳健性．

［1］ Vining G G，Myers R H. Combining Taguchi and response surface philosophies：A dual response approach[J]. Journal of Quality Technology，1990，22(1)：38-45.

［2］ Derringer G C，Suich R. Simultaneous optimization of several response variables[J]. Journal of Quality Technology，1980，12(4)：214-219.

［3］ Pignatiello J J. Strategies for robust multiresponse quality engineering [J]. IIE Transactions，1993，25(3)：5-15.

［4］ Vining G G. A compromise approach to multiresponse optimization[J]. Journal of Quality Technology，1998，30(4)：309-313.

［5］ Ko Y H，Kim K J，Jun C H. A new loss function-based method for multiresponse optimization[J]. Journal of Quality Technology，2005，37(1)：50-59.

［6］ Khuri A I，Conlon M. Simultaneous optimization of multiple responses represented by polynomial regression functions[J]. Technometrics，1981，23(4)：363-375.

［7］ Park K S，Kim K J. Optimizing multi-response surface problems：How to use multi-objective optimization techniques[J]. IIE Transactions，2005，37(6)：523-532.

［8］ Onur Köksoy. A nonlinear programming solution to robust multi-response quality problem[J]. Applied Mathematics and Computation，2008，196(2)：603-612.

［9］ Beyer H G，Sendhoff B. Robust optimization—A comprehensive survey[J]. Computer Methods in Applied Mechanics and Engineering，2007，196(33/34)：3190-3218.［10］ Myers R H，Montgomery D C. Response Surface Methodology[M]. 2nd ed. New York：John Wiley & Sons，2002.

［11］ Wang Jing，He Zhen，Oh J H，et al. Multi-response robust optimization using desirability function[C] // IEEE Symposium on Advanced Management of Information for Globalized Enterprises. Tianjin，China，2008：313-315.