广义非线性互补问题的非光滑牛顿算法＊

李梅霞，田治平

（潍坊学院，山东 潍坊 261061；山东科技职业学院，山东 潍坊 261053）

广义非线性互补问题的非光滑牛顿算法＊

李梅霞，田治平

（潍坊学院，山东 潍坊 261061；山东科技职业学院，山东 潍坊 261053）

研究了一类在多项式锥上的广义非线性互补问题。借助罚FB互补函数建立了该类问题的非光滑方程，提出了求解该方程的非光滑牛顿算法，证明了与互补函数有关的稳定点即为广义非线性互补问题的解。在较弱的条件下给出了牛顿算法的全局和超线性收敛性。

广义非线性互补问题；罚FB互补函数；稳定点；超线性收敛

1 引言

考虑广义非线性互补问题（简记为GNCP（F，G，κ））：寻求向量x＊∈Rn使得

其中F，G：Rn→Rm，κ⊆Rm为非空闭凸锥，κ0为κ的极锥。

广义非线性互补问题在工程和经济中具有广泛的应用。近几年来，其理论和算法都得到了较快发展〔1〕。特别地，当κ＝且G（x）＝x时，广义非线性互补问题即为传统的非线性互补问题［2］。

在本文中，我们将考虑一类特殊的广义非线性互补问题，即m＝n，F和G均为Rn上的连续可微函数，κ为Rn上的多项式锥，即存在A∈Rs×n使得

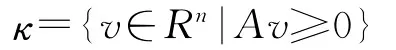
易证κ的极锥为

对于A＝I的情况，文献［3］中应用一类互补函数研究了该类问题的解与无约束极小化问题的最优解之间的关系。而对于κ＝｛v∈Rn｜Av≥0，Bv＝0｝的情况，文献［4］中应用FB互补函数进行了研究，证明了与互补函数有关的稳定点即为广义互补问题的解。同时给出了求解对应非光滑方程的非光滑L－M方法，证明了算法的全局收敛性和超线性收敛速度。在本文中，我们将应用罚FB函数［5］研究GNCP（F，G，κ）。众所周知，罚FB函数具有许多优良性质，借助该类函数我们建立了GNCP（F，G，κ）的非光滑方程，给出了求解该类方程的非光滑牛顿算法，在算法中我们应用了非单调线搜索，这些都使得算法具有较好的收敛性和较快的收敛速度。理论结果显示，（a）与互补函数有关的稳定点即为GNCP（F，G，κ）的解；（b）非光滑牛顿算法具有全局和超线性收敛性。

2 预备知识

本部分将给出一些基本概念及其性质。首先引入罚FB函数。对任意的a，b∈R，φ：R2→R称为罚FB函数，其形式为：

其中，x＋＝max｛0，x｝。

对任意的a，b∈Rn，定义

显然有下式成立

定义向量值函数Ψρ：Rn＋s→Rn＋s和实值函数Hρ：Rn＋s→R如下：

Ψρ（x，λ）具有以下性质：

定理1 x＊为GNCP（F，G，κ）的解当且仅当存在λ＊∈Rs，使得Ψρ（x，λ）＝0。

下面的定义和定理在后面的证明中将会用到。

定义1 若n×n矩阵M的每一个主子式都是非负的，则称矩阵M为P0－矩阵。若n×n矩阵M的每一个主子式都是正的，则称矩阵M为P-矩阵。

关于P（P0）-矩阵的性质及应用请参见文献［6］。

对任意的a∈Rn，定义Da＝diag（ai）为第i个对角元素为ai的对角矩阵。根据文献［7］中相关定理的证明可得下面的引理。

引理1 （a）设M为P0－矩阵，Da，Db⊆Rn×n为正定对角矩阵，则矩阵Da＋DbM为非奇异的。

（b）设M为P-矩阵，Da，Db⊆Rn×n为半正定对角矩阵并且Da＋Db是正定的，则矩阵Da＋DbM为非奇异的。

下面引入半光滑函数的有关定义和性质。

设Θ：Rn→Rm为一个局部Lipschitz连续函数，定义∂Θ（x）为Θ（x）在x∈Rn的Clarke广义雅克比，∂Θ（x）可以表示为

定义2［8］设Θ（x）：Rn→Rm是一个局部Lipschitz连续函数，若

存在，则称Θ（x）在x∈Rn是半光滑的。

定义3［8］设Θ（x）：Rn→Rm在x∈Rn是半光滑的并且对任意的V∈∂Θ（x＋h）和h→0，有

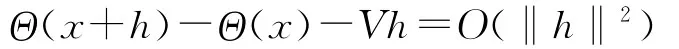
则称Θ（x）在x∈Rn是强半光滑的。

引理2［8］设Θ（x）：Rn→Rm是一个局部Lipschitz连续的半光滑函数，则

（a）对任意的V∈∂Θ（x＋h），h→0，有

（b）对任意的h→0，有

引理3［5］对任意的x∈Rn和λ∈Rs，有

其中，Da（x）＝diag｛ai（x）｝，Db（x）＝diag｛bi（x）｝，ai（x），bi（x）如下所示：

若［λ］2i＋［AF（x）］2i＞0，则

引理4［5］对式（2）和式（3）中定义的向量值函数Ψρ和实值函数Hρ，下面的结论成立。

（a）若F和G都是连续可微的，则Ψρ是半光滑的；若又有F′和G′都是局部Lipschitz的，则Ψρ是强半光滑的。

（b）若F和G都是连续可微的，则Hp是连续可微的，并且

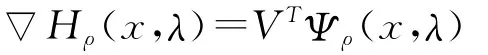
其中，V∈∂Ψρ（x，λ）。

定义4 设函数Θ（x）：Rn→Rn，若对任意的x∈Rn，V∈∂Θ（x）是非奇异的，则称Θ（x）是BD正则的。

3 稳定点与非奇异性条件

由定理1知，x＊为式（1）的解当且仅当z＊＝（x＊，λ＊）为无约束优化问题的全局最优值点且最优值为0。

定理2 设Z＊＝（X＊，λ＊）为式（4）的稳定点，F′（x＊）是非奇异的，并且G′（x＊）［F′（x＊）］－1是正定的，则x＊是GNCP（F，G，κ）的解。

证明：令U＊＝Φρ（AF（x＊），λ＊），V＊＝G（x＊）－ATλ＊，M＊＝G′（x＊）［F′（x＊）］－1

因为z＊＝（x＊，λ＊）是式（4）的稳定点，则▽Hρ（z＊）＝0。

由引理3和引理4知

计算可得

已知F′（x＊）非奇异，由式（5）和式（6）得

式（7）的两端同时左乘V＊T可得

将式（8）代人式（9）得

由引理3知DaDb是半正定的并且已知M＊是正定的，故由式（10）得

将式（11）代入式（7）和式（8）得

由式（11）和式（14）知x＊是GNC（F，G，κ）的解。

定理3 设z＝（x，λ）∈Rn×Rs，若G′（x）是非奇异的，AF′（x）［G′（x）］－1AT是P-阵，则对任意的V∈∂Ψρ（z），V是非奇异的并且z是GNCP（F，G，κ）的解。

证明：由于

已知AF′（x）［G′（x）］－1AT是P-阵，根据引理1知Db＋A［F′（x）G′（x）－1］TATDa是非奇异的，又因为G′（x）是非奇异的，所以VT是非奇异的，即V是非奇异的。

进一步，由引理3知0＝▽Hρ（x，λ）＝VTΨρ（x，λ），故Ψρ（z）＝0，所以z为GNCP（F，G，κ）的解。

4 算法及收敛性分析

在本部分中，我们将给出求解GNCP（F，G，κ）的带非单调步长的非光滑牛顿算法，并证明它的收敛性和收敛速度。

算法1

Step0 初始化：取z0∈Rn＋s，σ，β，ρ∈（0，1），ε≥0，a＝10，M≥1为正整数，k：＝0。

Step1 若‖▽Hρ（zk）‖≤ε，停；否则，转Step2。

Step2 选取Vk∈∂Ψρ（zk）。求dk∈Rn＋s满足下述线性系统，

其中，μk＝‖Ψρ（zk）‖，令α＝a。

下面给出求V∈∂Ψρ（z）的算法。

算法2

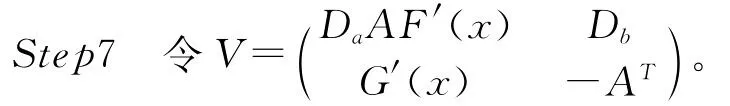
根据文献［4］和文献［9］中相关定理的证明可得到如下定理。

定理4 设｛zk｝是由算法1产生的序列，则｛zk｝的任何聚点均为式（4）的稳定点。

定理5 设｛zk｝是由算法2产生的序列，z＊是｛zk｝的一个聚点并且是Ψρ（z）＝0的BD正则解，则

（a）｛zk｝超线性收敛到z＊。

（b）若F′和G′又是Lipschitz连续的，则｛zk｝Q－二次收敛到z＊。

［1］Jiang H Y，Fukushima M，Qi L Q，et al.A trust region method for solving generalized complementarity problems［J］.SIAM J Optim，1998，8（1）：140－157.

［2］Facchinei F，Pang J S.Finite－dimensional variational inequalities and complementarity problems［M］.New York：Springer，2003.

［3］Kanzow C，Fukushima M.Equivalence of the generalized complementarity problem to differentiable unconstrained minimization［J］.J Optim Theory Appl，1996，90（3）：581－603.

［4］Wang Y J，Ma F M，Zhang J Z.A nonsmooth L－M method for solving the generalized nonlinear complementarity problem［J］.Appl Math Optim，2005，52（1）：73－92.

［5］Chen B T，Chen X J，Kanzow C.A penalized fischer－burmeister NCP－function［J］.Math Prog，2000，88（1）：211－216.

［6］Cottle R W，Pang J S，Stone R E.The linear complementarity problem［M］.New York：Academic Press，1992.

［7］Kanzow C，Kleinmichel H.A new class of semismooth Newton－type methods for nonlinear omplementarity problems［J］.Comput Optim Appl，1998，11（3）：227－251.

［8］Qi L Q，Sun J.A nonsmooth version of Newton’s method［J］.Math Programming，1993，58（3）：353－367.

［9］Li M X，Wang C Y.Convergence property of gradient－type methods with non－monotone line search in the presence of perturbation［J］.Appl Math Optim，2006，174（2）：854－868.

（责任编辑：肖恩忠）

A Nonsmooth Newton Method for Solving the Generalized Nonlinear Complementarity Problem

LI Mei－xia，TIAN Zhi－ping
（Weifang University，Weifang 261061，China；Shandong Vocational College of Science ＆Technology，Weifang 261053，China）

In this paper，the generalized nonlinear complementarity problem（abbr.GNCP）defined on a polyhedral cone is studied.Based on a penalized FB NCP－function a system of nonsmooth equations is built and the nonsmooth Newton algorithm is presented for solving this system.We prove that the stationary points of the penalized FB merit function are the solution of the GNCP.Under mild assumptions，we show that the Newton algorithm is both globally and superlinearly convergent.

GNCP，penalized FB NCP－function，stationary point，superlinear convergence

2011－04－26

国家自然科学基金资助项目（10901096）；山东省自然科学基金资助项目（ZR2009AL019）

李梅霞（1970－），女，山东高密人，潍坊学院数学与信息科学学院副教授，博士。研究方向：最优化方法及其应用。

O221.2 文献标识码：A 文章编号：1671－4288（2011）06－0006－05