非自治退化抛物方程柯西问题熵解的存在性＊

郝兴文

（潍坊学院，山东 潍坊 261061）

非自治退化抛物方程柯西问题熵解的存在性＊

郝兴文

（潍坊学院，山东 潍坊 261061）

非自治的二阶退化抛物型方程是物理、金融中常见的数学模型。本文将利用粘性消去法，证明这类方程的柯西问题熵解的存在性。

退化抛物方程；熵解；柯西问题

1 问题与主要结果

考虑如下非自治退化抛物方程的柯西问题：

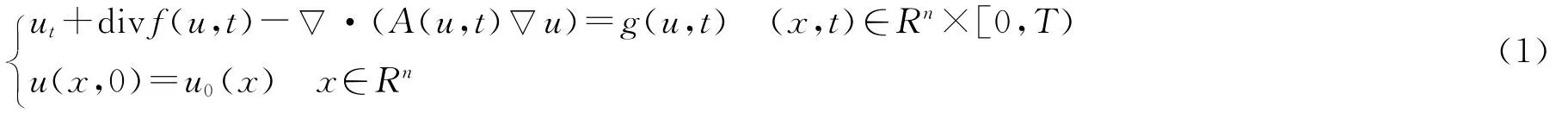
式中，u为未知函数；T为R＋上任意时刻。f（u，t）＝（f1（u，t），f2（u，t），…，fn（u，t））是流函数，A（u，t）是对称、非负定矩阵，其元素可以写成aij＝∑kk＝1σikσkj。在本文中，假定fi，aij，g具备所需的光滑性，且g（0）＝0。这个模型可以用来描述许多现象，如多孔介质中的热传输［1］、沉降－凝固过程［2］、金融决策［3］等。方程（1）是下列一般形式的退化抛物－双曲方程的一个特殊形式，

由于这个方程的解有间断，大家在不同的解空间寻找弱解，例如文献［8］中给出了方程（2）的BV解的存在性，文献［4］中得到了在方程（2）中不显含x，t形式的方程动力学解的存在唯一性，其它形式的解可以见文献［5－7，9－10］。本文将利用粘性消去法，证明方程（1）的L1熵解的存在性。在给出主要结果之前，首先给出一些必要地符号和方程（1）的熵解的定义。

对任意的凸函数S，记

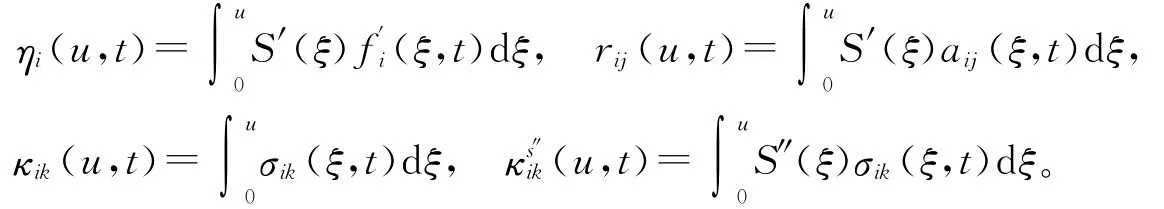
定义1 一个可测函数u∈L∞（［0，T）×Rn）∩L∞（［0，T），L1（Rn））是方程（1）的熵解，如果u满足：

（2）对任意的κ＝1，2，…，K以及φ∈C（R），下面的链式法则成立

（3）对任意的φ∈C（R），φ≥0，下列关系式成立

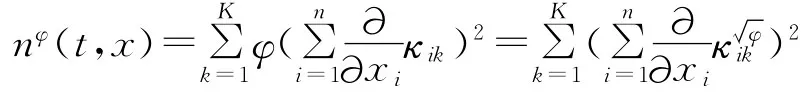
（4）对任意的凸函数S（u），熵不等式在D′（［0，T）×Rn）中成立

并且满足S（u）｜t＝0＝S（u0）。

定理1 如果初值u0（x）∈W2，1（Rn）∩H1（Rn）∩L∞（Rn），则方程（1）存在熵解u∈L∞（［0，T）×Rn）∩L∞（［0，T），L1（Rn））。

注：借助于熵解的收缩性，可以证明初值u0∈L1（Rn）∩L∞（Rn）时，熵解的存在性以及唯一性。

2 定理的证明

在证明定理之前，首先给出粘性方程光滑解的先验估计。考虑如下方程

其中，I是单位矩阵。其柯西问题的解具有下列估计。

引理 设uε是方程（3）的柯西问题的C2光滑解，那么存在常数M1，M2，使得下列不等式成立

证明 （1）式可以由Volpert—Hudjaev定理直接得到。下面证明（2）式成立。

在方程（3）两边同乘以wλ（x）sgn u，然后在［0，T）×Rn上积分，得到

这里，σij是Christoffel记号。经过计算，可以得到

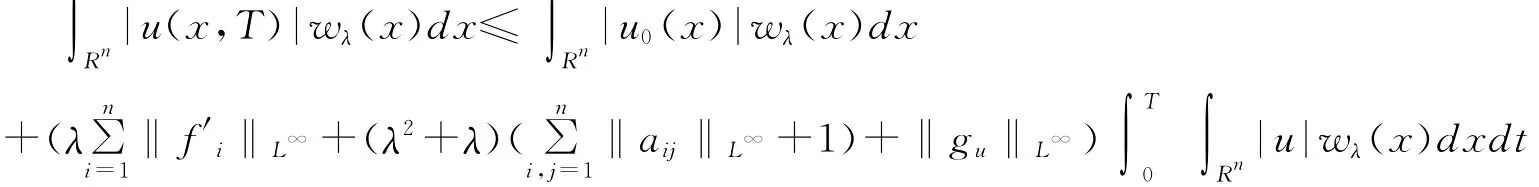
利用Gronwall不等式，得

在上式中令λ→0，利用法图引理和勒贝格控制收敛定理，得

证毕。（2）和（3）的证明与（1）类似，我们略去其过程。

由紧嵌入定理可知，存在uε的子列（仍记为uε）及函数u，使得

下面证明u是（1）的熵解。由于初值u0∈L1（Rn）∩L2（Rn）∩L∞（Rn），可知

事实上，对于任意凸函数S（u），在D′（［0，T）×Rn）中，uε满足下式

［1］Juan L V.The Porous Medium Equation：Mathematical Theory［M］.London：Oxford University Press，2006.

［2］Bustos M C，Concha F，Bürger R，et.al.Sedimentation and Thicking：Phenomenological Foundation and Mathematical Theory［M］.Dordrecht：Kluwer Academic Publishers，1999.

［3］Antonelli F，Barucci E，Mancino M E.A comparison result for FBSDE with applications to decisions theory［J］.Math Meth Oper Res，2001，54（3）：407－423.

［4］Chen G Q，Perthame B.Well－posedness for non－isotropic degenerate parabolic－hyperbolic equation［J］.Analyse nonlineaire，2003，20（4）：645－668.

［5］Carrillo J.Entropy solutions for nonlinear degenerate problems［J］.Arch Rational Mech Anal，1999，147（4）：269－361.

［6］Bendahmane M，Karlsen K H.Renormalized entropy solutions for quasilinear anisotropic degenerate parabolic equations［J］.SIAM J Math Anal，2004，36（2）：405－422.

［7］Perthame B，Souganidis P E.Dissipative and entropy solutions to non－isotropic degenerate parabolic balance laws［J］.Arch Rational Mech Anal，2003，170（4）：359－370.

［8］Volpert A I，Hugjaev S I.Cauchy’s problem for degenerate second order quasilinear parabolic equation［J］.Transl Math USSR Sb，1969，7（3）：365－387.

［9］Wu Z，Zhao J，Yin J，et al.Nonlinear Diffusion Equation［M］.Chennai：World Scientific Publishing，2001.

［10］Chen G Q，Karlsen K.Quasilinear anisotropic degenerate parabolic equations with time－space dependent diffusion coefficients［J］.Commun Pure Appl Anal，2005，4（2）：241－266.

（责任编辑：肖恩忠）

Existence of the Entropy Solutions to Cauchy Problem for Autonomous Degenerate Parabolic Equation

HAO Xing－wen
（Weifang University，Weifang 261061，China）

Second order degenerate parabolic equation models many phenomenons arising in physics and financial decision etc.In this paper，existence of entropy solution to cauchy problem is obtained by the a prior estimates of the smooth solutions to the viscous equation.

degenerate parabolic equation，entropy solutions，cauchy problem

2010－08－10

国家自然科学基金资助项目（10571120）；潍坊学院博士基金项目（2011BS11）

郝兴文（1973－），男，山东潍坊人，潍坊学院数学与信息科学学院讲师，博士。研究方向：非线性偏微分方程。

O175.27 文献标识码：A 文章编号：1671－4288（2011）06－0020－03