一类磁滞动力学方程的辐角稳定性判别法

杜　红,　于存光

(黑龙江科技学院 理学院, 哈尔滨 150027)



一类磁滞动力学方程的辐角稳定性判别法

杜红,于存光

(黑龙江科技学院 理学院, 哈尔滨 150027)

笔者利用分布切削力的特性建立的一种磁滞动力学微分-积分方程为例，提出了一种新的稳定性判别法，给出动力学方程渐近稳定条件及稳定性判别理论，通过计算特征方程的辐角变化量来判别方法的稳定性。该方法计算简单，可以成为切削加工的稳定性理论研究的一种新判别方法。

微分-积分方程; 幅角原理; 稳定性

0　引　言

力-热耦合模型是基于在切削过程中加工材料本构关系、温度等物理特性对系统稳定性的影响提出的一种颤振形式。切削过程是切削工具和工件之间动力交换的结果。因此,在数学描述中要考虑到切屑的几何形状、工件的力学及热力学性质等。在切削过程中,存在Coulomb摩擦或材料的弹塑性产生磁滞现象,2001年,G.Stépan[1]考虑了切削力的分布特征,得到了切削力变化和切削厚度变化之间的黏弹性关系,建立了一个线性时滞微分-积分方程。2002年,Kalmar-Nagy在车削加工中系统阐述了由于Coulomb摩擦或加工材料本身的弹塑性也会引发振动,基于磁滞回复力谐振子模型,建立了一阶磁滞微分方程[2]。Poddar、Pratap和Moon等提出了磁滞切削力[3-5],给出了分片线性磁滞力模型。Caughey[6]和Iwan[7]考虑了带有磁滞无阻尼摆的切削力的振动,给出了周期与准周期运动的磁滞环。

稳定Lobe图能很好的体现偏微分方程平衡点的稳定性。构造稳定性图的方法主要有Stépn提出的D曲线法[8]、时间有限元法[9]、半离散法(Semi-discret ization method)[10]和全离散法[11]。笔者将利用分布切削力的特性建立的反映磁滞现象的动力学方程为例,探究动力学系统稳定性分析的幅角判别方法,通过计算特征方程的幅角变化量来判别方程的稳定性。

1　方程的建立

(1)

式中,ωn是无阻尼振动的角频率,ζ是阻尼系数,x(t)为位移,xτ表示x(t)的延迟量,切削力系数k1是在标准切厚切削力变化率。

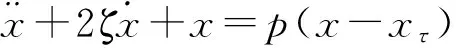
其中

该方程也被称为典型的线性模型。

如图1所示,考虑作用在刀具前刀面的切削力的分布,建立磁滞动力学微分-积分方程[2]。

图1　刀具上切削力分布Fig. 1　Distribution of cutting force on tools

图1中s是局部坐标,表示从s=0到切片卷曲离开刀具s=l的可测距离。W(s)是切屑形状函数,是标准形状函数,因此

(2)

(3)

Stépn将切削力表示成

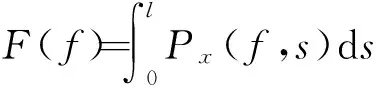
(4)

稳定切削过程中,对于标准切削厚度f0,切削力则为

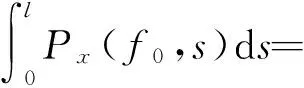
(5)

设切屑流动速度为

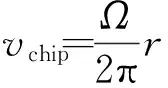
(6)

r为工件半径,Ω为主轴旋转角速度,那么,切屑流到刀具所需的时间

(7)

记再生延迟时间为

(8)

故τ和h的比率是常数

(9)

当这个比率很小时,h被称为短延迟。

因为切片厚度为f=f0+Δf,切片厚度是时间的函数,因此,为考虑切片运动,引入局部时间θ

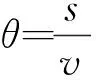
(10)

应力分布函数w表示为:

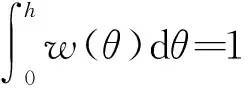
(11)

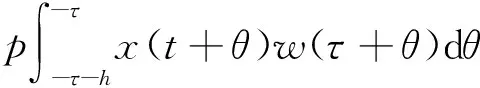
(12)

利用变量代换,式(12)的右端变换为

这里仍沿用原式积分变量,故式(12)为

(13)

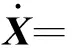
即

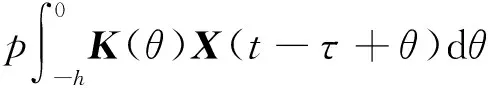
(14)

其中,x(θ)=φ(θ),-h<θ≤0,X(t)∈Rn,R(θ),K(θ)∈Rn×n,φ(θ)∈C1(-h,0]。矩阵R(θ)=(rij),K(θ)=(kij)满足

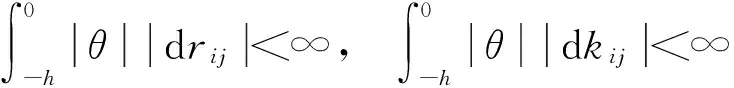
i,j=1,2,…,n,

(15)

令

(16)

对式(16)进行Laplace变换,得到特征方程:

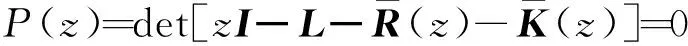
(17)

2　主要结果

引理2(Brown辐角原理[13])设曲线C是一条闭曲线,函数f(z)满足

(1)f(z)在C的内部除了极点外是解析的;

(2)f(z)在C上解析且不为零;

(3)Z是C的内部零点的个数,Y是C的内部极点的个数;

则

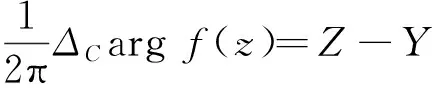
其中ΔCargf(z)=argf(c2)-argf(c1),c1,c2分别为曲线的起点和终点。

证明z是方程(14)在右半平面Rz≥0的特征根,有

定理结论成立。

记la为两点d1=(r,π/2),d2=(r,-π/2)在虚轴上的直线段,

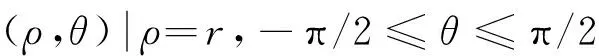
图2　D和Q区域Fig. 2　D and Q area

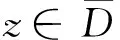
定理2在引理1的条件下,系统(14)是渐进稳定的充要条件是

P(z)≠0,z∈l,

(18)

和

ΔlargP(z)=0,其中ΔlargP(z)为P(z)沿曲线l一周辐角的变化量。

证明先证必要性。假设系统(14)是渐进稳定的。即特征方程P(z)的所有零点都在左半平面,故当z∈l时,P(z)≠0,P(z)沿曲线l一周辐角的变化量为零。

定理2′在引理1的条件下,系统(14)是渐进稳定的充要条件是

P(z)≠0,z∈d1O,

(19)

和

Δl′argP(z)=0,

其中O=(0,0)。

定理3在引理1的条件下,如果

P(z)≠0,z∈d1O,

(20)

和

(21)

系统(14)是不稳定的。其中Z是系统不稳定特征根的个数。

3　数值实验

以下给出系统(12)的稳定性判定实验,对应不同的参数计算系统的特征函数P(z)沿曲线l′一周相平面图。

对于式(12),取形状函数为

θ∈(-∞,0],

(22)

其中l0表示有效接触长度,q0为短延迟比率。将式(12)两边对t求导,并利用分部积分得到

(1+p)x(t)-px(t-τ)=0,

(23)

得到式(23)的特征方程为

D(λ)=q0τλ3+(1+2ζq0τ)λ2+(2ζ+q0τ)λ+

(1+p)-pe-λτ=0。

(24)

当m=50kg,ζ=0.05,ωn=775rad/s,q0=0.01时,按照文中给出的判别方法,取k1=3.36×107,Ω=300和Ω=1 000时,式(15)的相平面图见图3,稳定图见图4。

图3中P(z)的相曲线与虚轴有交点或包含原点O=(0,0),则系统不稳定,并且不稳定根的个数为相曲线包含原点的周数,也为P(z)沿曲线l′一周辐角变化量2π的倍数。如果P(z)的相平面在右半平面变化,则系统是稳定的。利用文中给出的判别法,最终可给出系统(12)的稳定性图。

图3　相曲线P(z)图Fig. 3　Phase graph of P(z)

图4　特征方程(24)的稳定图Fig. 4　Stability figure of characteristic equations (24)

[1]STÉPAN G. Modelling nonlinear regenerative effects in metal cutting[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2001, 359(1781): 739-757.

[3]PODDAR B, MOON F C, MUKHERJEE S. Chaotic motion of an elastic-plastic beam[J]. Journal of Applied Mechanics, Transactions ASME, 1988, 55(1): 185-189.

[4]PRATAP R, MUKHERJEE S, MOON F C. Dynamic behavior of a bilinear hysteretic elasto-plastic oscillator, part II: oscillations under periodic impulse forcing[J]. Journal of Sound and Vibration, 1994, 172(3): 339-358.

[5]MOON F C, KALMR-NAGY T. nonlinear models for complex dynamics in cutting materials[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2001, 359(1781): 695-711.

[6]CAUGHEY T K. Sinusoidal excitation of a system with bilinear hysteresis[J]. Journal of Applied Mechanics, 1960, 27(4): 640-643.

[7]IWAN W D. The steady-state response of a two-degree-of-freedom bilinear hysteretic system[J]. Journal of Applied Mechanics, Transactions ASME, 1965, 32(1): 151-156.

[9]BAYLY P V, HALLEY J E, MANN B P. Stability of interrupted cutting by temporal finite element analysis[J]. Journal of Manufacturing Science and Engineering, 2003, 125(2): 220-225.

[10]MANN B P, YOUNG K A. An empirical approach for delayed oscillator stability and parametric identification[J]. Proceedings of the Royal Society A,Mathematical, Physical and Engineering Sciences, 2006, 462(2071): 2145-2160.

[11]DING YE, ZHU LIMIN, ZHANG XIAOJIAN, et al. A full-discretization method for prediction of milling stability[J]. International Journal of Machine Tools and Manufacture, 2010, 50(5): 502-509.

[12]KOLMANOVSKII V B, MYSHKIS A. Applied theory of functional differential equations[M]. Dordrecht: Kluwer Academic Publishers, 1992.

[13]BROWN J W, CHURCHILL R V. Complex variables and applications[M]. 7th ed.Beijing: McGraw-Hill Companies, Inc. and China Machine Press, 2004.

(编辑徐岩)

Argument stability criterion method of a hysteresis dynamic equation

DUHong,YUCunguang

(College of Sciences, Heilongjiang Institute of Science & Technology, Harbin 150027, China)

This paper proposes a new stability criterion method, based on a hysteresis dynamic differential-integral equation derived from using properties of distributed cutting force. The paper offers asymptotically stable conditions for Kinetic equation and stability criterion theories and identifies stability of systems by calculating change in argument of characteristic equation. The method features an easy operation and promises as a new criterion method for theoretical study of stability of cutting process.

differential-integral equation; argument principle; stability

1671-0118(2012)03-0325-05

2012-04-30

国家自然科学基金项目(51105135)；黑龙江省自然科学基金项目(A201015)

杜红(1972-),女，黑龙江省密山人，教授，博士后，研究方向：再生核、小波分析在图像处理中的应用，E-mail:du_hong163@163.com。

O175.6;O175.13

A