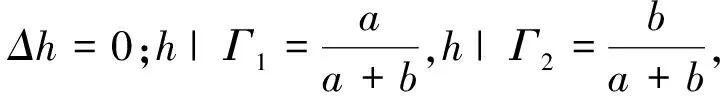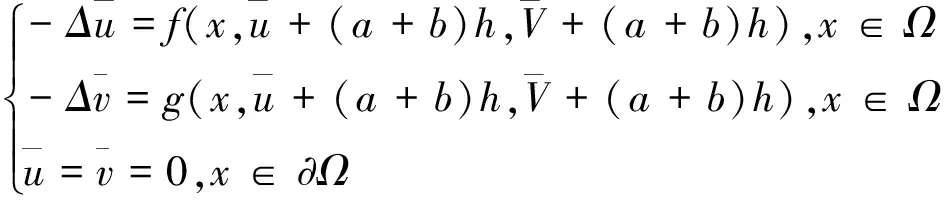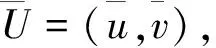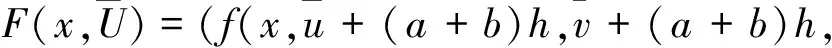一类半线性椭圆方程组正解的存在性与唯一性
赵建清
(连云港师范高等专科学校 数学与信息工程学院,江苏 连云港 222000)
源于文献[1,2]的启发,本文主要采用不动点定理及Leray-schauder度性质考察如下方程组在一定条件下正解的存在性,不存在性和唯一性等性质.同时对[3]的结果进行了修改和完善.
-Δu=g(x,v),-Δv=f(x,u),x∈Ω;
u=v=0,x∈Γ1,u=v=b,x∈Γ2
(1)
-Δu=f(x,u,v),-Δv=g(x,u,v),x∈Ω;
u=v=a,x∈Γ1,u=v=b,x∈Γ2
(2)
-Δu=g(x,v),-Δv=f(x,u),x∈Ω;
u=v=b,x∈Γ2,u=v=a,x∈Γ1
(3)
其中Ω⊂Rn是有界洞型区域,内边界为Γ2,外边界为Γ1,且∂Ω=Γ1∪Γ2光滑,a,b>0是常数.
1 两个引理
假设如下条件成立:
(H1)f,g:R→R当n=1时连续,且当n≥2时具有指数β∈(0,1]的局部Holder连续性;


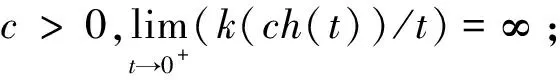
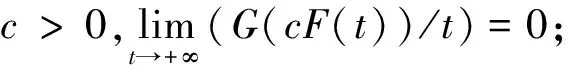
(H5)t∈(-∞,0]→f(x,t)单调非增,t∈(-∞,0]→g(x,t)单调非增;

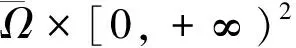
(H8)0≤f(x,s,t),g(x,s,t)≤c,c为正常数;
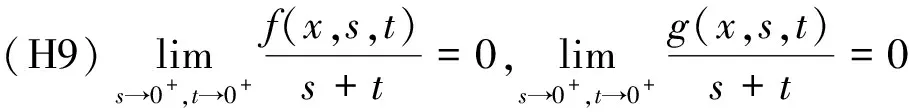
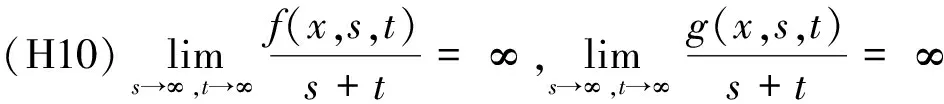
(H11)f(x,s,t),g(x,s,t)分别关于s,t单调增;

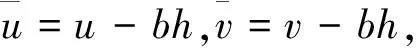
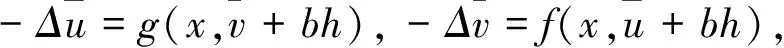
(4)
显然,若问题(4)有非负解,则问题(1)有正解.这里Ω∈C2,α,α∈(0,1].
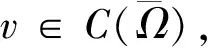
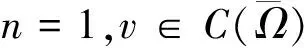
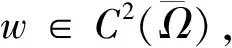

证明 (1)这是一个典型结果.有-Δw=v,x∈Ω;w=0,x∈∂Ω.
(2)的结果可从最大值原理和边界点引理得到.

-Δψ=1,x∈Ω,ψ=0,x∈∂Ω.
引理2f,g满足(H1),(H2),(H5)和(H6),则存在常数M>0有max(‖u‖∞,‖v‖∞)≤M,对所有问题-Δu=tg(x,v+bh),x∈Ω,-Δv=tf(x,u+bh),x∈Ω,u=v=0,x∈∂Ω,t∈[0,1](1.1t)的解成立.


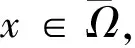
假设若‖u‖∞>A,‖v‖∞>A,使用相同的条件我们得到
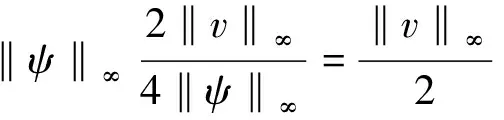
从而得到‖v‖∞≤0这与‖v‖∞>A相矛盾.
2 主要结果
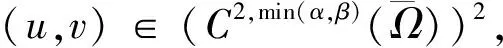

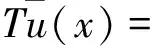
另一方面,我们有
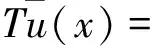
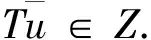
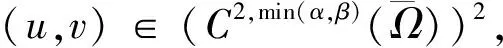


定义映射为Lt:Y→Y.

易知对于t∈[0,1],Lt是紧的.令M是引理2中的常数.
考虑球BM⊂Y:BM={(u,v)∈Y;‖(u,v)‖ (5) 显然,问题(5)有非负解,则问题(2)有正解. 于是(5)化为向量形式: 设问题(2)中函数满足(H7)-(H12)的条件. 推论1 若条件(H7),(H8)成立,则问题(5)存在一个有界非负解.即方程组(2)存在一个正解. 推论2 若条件(H7),(H9),(H10),(H11)成立,则存在正数K,使当a+b 推论3 若条件(H12)成立,则问题(2)最多只有一个解. 以上推论的证明可采用文献[2]中作者的证明方法,只需将b用a+b替换即可. 由此方法的启发我们可研究方程组(3)的正解的存在性. 参考文献: [1]Robert Dalmasso.Existence and uniqueness of positive solutions of semilinear elliptic systems [J].Nonlinear Analysis,2000,39:559-568. [2]钟金标,陈祖墀.有界洞型区域内半线性椭圆方程组的正解[J].中国科学技术大学学报,2002,32(1):30-36. [3]伍明珠,赵建清.有界洞型区域内一类半线性椭圆方程组的正解[J].乐山师范学院学报,2006,21(12):12-13.