邻近点CKQ法的强收敛性
李 强,冯世强,周 瑞
(西华师范大学数学与信息学院,四川南充 637009)
邻近点CKQ法的强收敛性
李 强,冯世强,周 瑞
(西华师范大学数学与信息学院,四川南充 637009)
引入了与邻近点算法(PPA)有关的新迭代序列,并利用CKQ法证明了这种迭代序列在一定的假设条件下强收敛.所得结论推广了有关文献中的相关结果.
邻近点算法;强收敛;CKQ法;非扩张映射;极大单调算子
设H是实Hilbert空间,多值算子A:H→2H的图像G(A)定义为G(A)={[u,v]:u ∈D(A),w∈A(u)},称A 为单调算子,如果G(A)是X×X*中的单调集,即〈u1-u2,w1-w2〉≥0,∀[ui,wi]∈G(A),i=1,2;单调算子A 称为极大单调算子,若G(A)不真包含于X×X*的任何单调集中.
对于极大单调算子A,r >0,令Jr=(I+rA)-1,则Jr称为A的预解算子,F(Jr)是Jr的不动点集.定义算子A的零点:S=A-1(0)={x ∈D(A):0∈Ax}.众所周知,如果A是极大单调的,那么其预解算子Jr是单值非扩张的,且对于所有的r>0,有F(Jr)=S.在本文中总假定A是极大单调的且零点集非空.
实Hilbert空间中,关于PPA问题,Rockafellar[1]首先定义序列⊂C 如下:

如果infn≥0cn>0,那么有xn→PSx0(弱).
随后,在文献[2-4]的启发下,Solodov等[5]证明了修正的迭代序列的强收敛性.给定x0∈C,定义序列⊂C 如下:
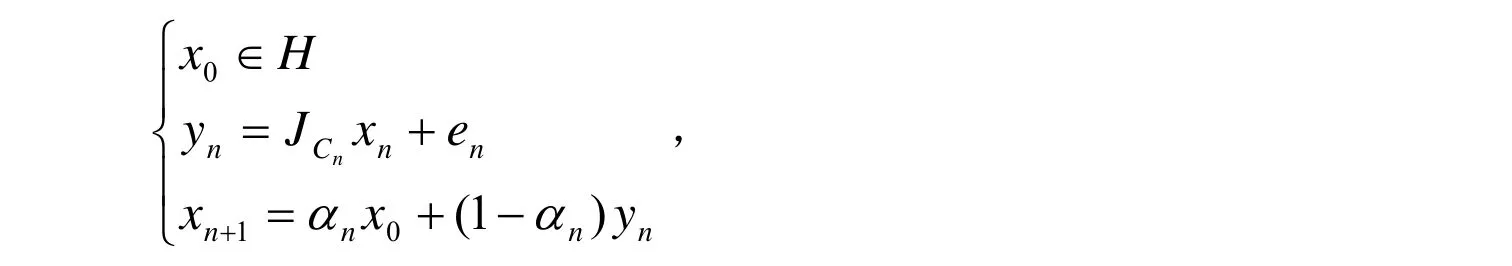
Xu[6]证明了极大单调算子Mann迭代的强收敛性.给定x0∈C,定义序列⊂C 为:xn+1=αnxn+(1-αn)Jcn(xn+en),如果(a)αn≤1-δ,δ∈(0,1),(b)cn→∞,(c)<∞,那么有x→Px(弱).其中e为误差序列.nS0n
笔者受文献[2,7-8]的启发,在实Hilbert空间中,为研究邻近点迭代序列的收敛性,把Mann迭代和近似迭代算法揉合在一起,修正了迭代序列,引入了CQ方法;另外,弱化了以上(a)–(d)的限制,并得到了强收敛.本文的迭代序列与文献[3]的有所不同,所得结论推广和改进了文献[3]的相关结果.
1 预备知识
引理1[8]设H是实Hilbert空间,对任意的u,v∈H,有
引理2[8]设H是实Hilbert空间,C是H的非空闭凸子集,点x,y,z属于H,a是实数,那么集合D=是闭凸集.
下面的引理是众所周知的.
引理3 设H是实Hilbert空间,C是H的非空闭凸子集,PC表示从H到C上的投影,即对任意的x∈H,给定x∈H和z∈C,那么z=PCx的充要条件是<x-z ,y-z>≤0对任意的y∈C都成立.
引理4[9]设H是实Hilbert空间,C是H的非空有界闭凸子集,T:C →C是一渐近非扩张映像,如果序列⊂C ,且满足x→z (弱)和x-Tx→0,那么z∈F(T).nnn
2 主要结果
定理1 设H是实Hilbert空间,C是H的非空闭凸子集,Jr:C→C是一非扩张映像且F(J)=S,给定x∈C,定义序列⊂C 如下:r0

证明:首先证明S⊂Cn.由引理2知,Cn与Kn都是凸集.对任意的p∈S,有:
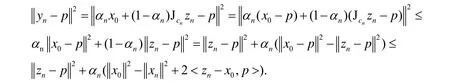
接下来证明S⊂Kn.对任意的p∈S,有:
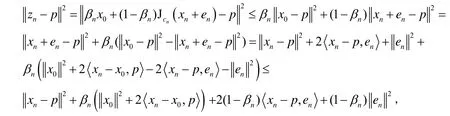
于是p∈Kn,从而S⊂Kn.
然后证明S⊂Qn.对n用数学归纳法:
1)当n=0时,S⊂Q0=C,显然成立;
2)假设S⊂Qn,需要证明S⊂Qn+1.由序列的定义xn+1=PCn∩Qn(x0)以及引理3,有<xn+1-z,x0-xn+1>≥0对任意的z∈Cn∩Kn∩Qn成立.根据以上结果知S⊂Cn∩Kn∩Qn,从而对所有的z∈S,<xn+1-z,x0-xn+1> ≥0也成立.又由(1)中Qn的定义可知,z∈Qn+1,从而有S⊂Qn+1.这表明S⊂Qn.
这样一来,就得到S⊂Cn∩Kn∩Qn.又注意到Qn={v∈C:<xn-v,xn-x0>≤0},即说明xn=PQnx0.再由前面已证的S⊂Qn,所以对任意的t ∈S,特别地,对t=PSx0,有:

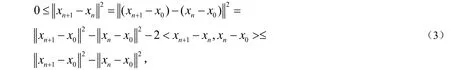


令c =infn≥0cn>0,由文献[6]的引理3.3可知,→0.假设对任意的且xnj→(弱),由引理4知,∈F(T).

定理2 设H是实Hilbert空间,C是H的非空闭凸子集,Jr:C→C是一非扩张映像且F(J)=S.给定x∈C,定义序列⊂C 如下:r0


由于xn+1∈Cn,从而由(6)式可知:
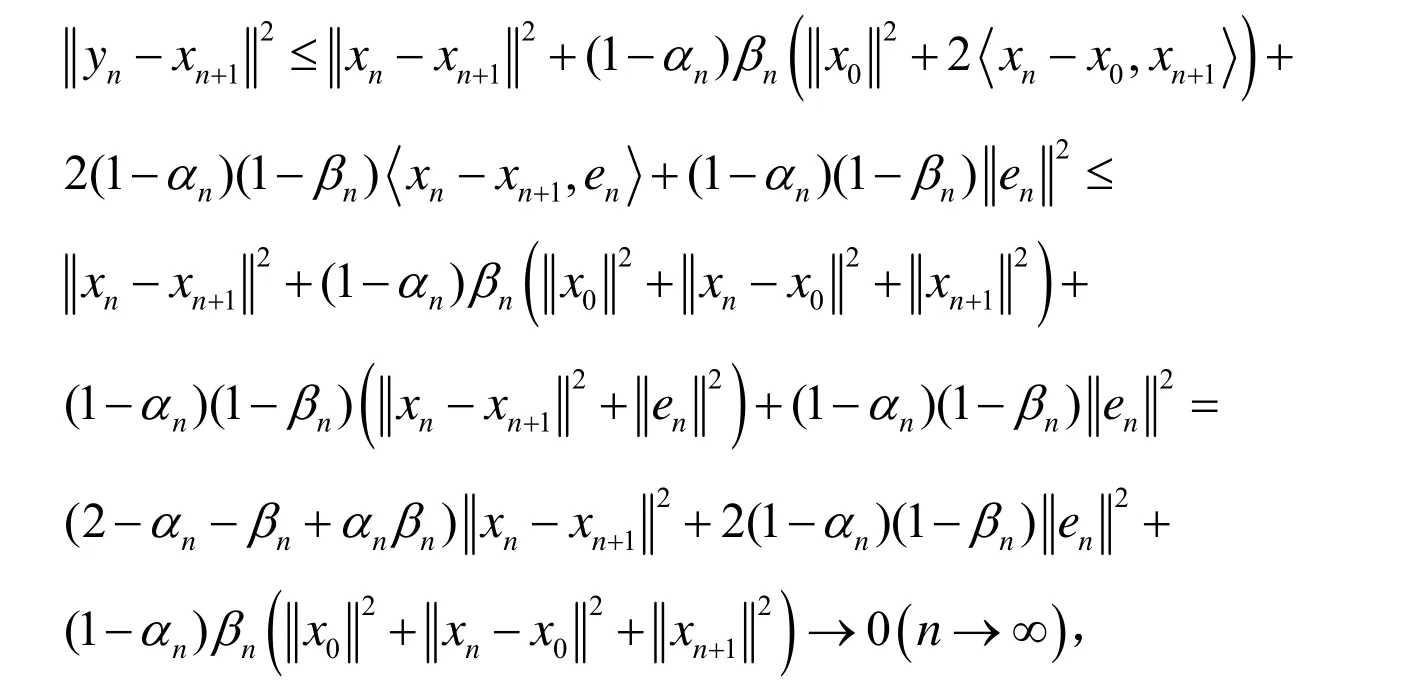

剩余的证明同定理1的类似,限于篇幅,这里从略.
[1] Rockafellar R T.Monotone operators and the proximal point algorithm [J].SIAM J Control Optim, 1976, 14:877-898.
[2] Nakajo K, Takahashi W.Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups [J].J Math Anal Appl, 2003, 279:372-379.
[3] Marino G, Xu H K.Convergence of generalized proximal point algorithms [J].Comm Pure Appl Anal, 2004, 3:791-808.
[4] Kamimura S, Takahashi W.Strong convergence of a proximal-type algorithm in a Banach space [J].SIAM J Optim, 2003, 13:938-945.
[5] Solodov M V, Svaiter B F.Forcing strong convergence of proximal point iterations in a Hilbert space [J].Math ProgrSer A, 2000, 87:189-202.
[6] Xu H K.Iterative algorithms for nonlinear operators [J].J London Math Soc, 2002, 66:240-256.
[7] Kim T H, Xu H K.Strong convergence of modified Mann iterations for asymptotically nonexpansive mappings and semigroups [J].Nonliear Anal, 2006, 64:1140-1152.
[8] Marino G, Xu H K.Strong convergence of the CQ method for fixed point iteration processes [J].Nonliear Anal, 2006, 64:2400-2411.
[9] Lin P K, Tan K K, Xu H K.Demiclosedness principle and asymptotic behavior for asymptotically nonexpansive mappings [J].Nonliear Anal, 1995, 24:929-946.
The Strong Convergence of the CKQ Method for the Proximal Point Algorithm
LI Qiang, FENG Shiqiang, ZHOU Rui
(College of Mathematics and Information, China West Normal University, Nanchong, China 637009)
In this paper, we introduced the new iterative sequence for proximal point algorithm.Employing the CKQ method, we proved the strong convergence for this kind of iterative sequence under suitable assumptions.The results presented in this paper extend corresponding results in relevant literature.
Proximal Point Algorithm;Strong Convergence;CKQ Method;Non-expansive Mapping;Maximal Monotone Operator
O232
A
1674-3563(2013)04-0018-06
10.3875/j.issn.1674-3563.2013.04.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:王一芳)
2012-11-14
教育部科学技术重点项目(211163)
李强(1986- ),男,山西太原人,硕士研究生,研究方向:优化与控制理论

