具阶段结构的食饵-捕食者扩散模型的稳定性

苗亮英，张 睿，刘志高，卢雪丽

（1.兰州交通大学数理与软件工程学院,甘肃兰州 730070；2.白银市工业学校,甘肃白银 730900）

具阶段结构的食饵-捕食者扩散模型的稳定性

苗亮英1，张 睿1，刘志高2，卢雪丽1

（1.兰州交通大学数理与软件工程学院,甘肃兰州 730070；2.白银市工业学校,甘肃白银 730900）

讨论了一类捕食者种群具有阶段结构的食饵-捕食者扩散模型，运用线性化方法和Lyapunov函数法讨论了该反应扩散模型非负平衡点的局部渐近稳定性和全局渐近稳定性.

食饵-捕食者模型；阶段结构；扩散；稳定性

本文考虑如下捕食者具阶段结构的食饵-捕食者模型：

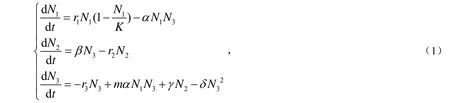
其中，N1为食饵种群密度，N2为幼年捕食者种群密度，N3为成年捕食者种群密度，r1为食饵种群的内禀增长率，K 为环境容纳量，α为捕食参数，m为捕食者种群的捕食率，r3为成年捕食者种群的死亡率，γ为由幼年捕食者种群转化为成年捕食者种群的比例常数，r2=μ+γ，μ为幼年捕食者种群的死亡率，β为幼年捕食者种群的出生率，δ为成年捕食者种群的密度制约系数.文献[1]中，作者给模型（1）加上捕获项后讨论了其非负平衡点的稳定性，获得了其持续生存的条件及最优收获策略.受文献[1]启发，本文考虑给模型（1）加上扩散项，之后再讨论其稳定性.

系统（2）描述了食饵-捕食者种群密度在空间分布均匀时的增长规律，当种群密度在空间分布不均匀时，同种群间为竞争资源等会从高密度区向低密度区扩散，于是得到如下反应扩散模型：

这里，Ω∈Rn是一个具有光滑边界∂Ω的有界区域，η是边界∂Ω的单位外法向量，=，正常数di（i=1,2,3）是对应于食饵u1和捕食者u2、u3的扩散系数，ui0（x）是在Ω上满足相容条件的光滑函数，齐次Neumann边界条件说明系统（3）是自封闭的.本文主要采用文献[2]的思想，应用线性化方法和构造Lyapunov函数方法来讨论系统（3）正平衡点的稳定性.

111323233132123容易得到系统（2）的平衡点分别为E0（0,0,0）和E1（a,0,0）；当e＞c时，系统（2）的平衡点为；当bc+af＞be ，e+ad＞c时，系统（2）的唯一正平衡点为

定理1 下面结论成立：

1）系统（2）的平衡点E0（0,0,0）无条件不稳定；

2）当1+c＞ad ，c＞ad+e时，系统（2）的平衡点E1（a,0,0）全局渐近稳定；

3）当bc+af＜be ，1+2e＞c 时，系统（2）的平衡点全局渐近稳定；

4）当bc+af＞be，e+ad＞c时，系统（2）的唯一正常数平衡点全局渐近稳定.

证明：由标准的线性化方法容易证明系统（2）各个平衡点的局部渐近稳定性.由于Lyapunov函数的构造和相应的计算比较困难，这里只给出E1,E2,E3点的全局渐近稳定性的证明.

设（u1,u2,u3）是系统（2）的任一正解，定义如下Lyapunov函数：

1 系统（2）的稳定性

令α2=eα3，bα1=dα3，当1+c＞ad ，c＞ad+e时，有：

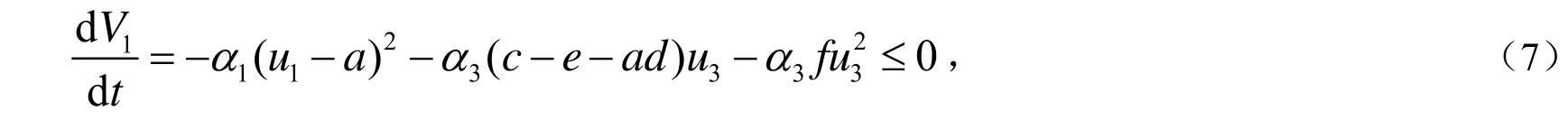
由Lyapunov-Lasalle不变原理知，当1+c＞ad，c＞ad+e时，平衡点E1（a,0,0）全局渐近稳定.

令α2=eα3，bα1=dα3，当bc+af＜be ，1+2e＞c时，有：

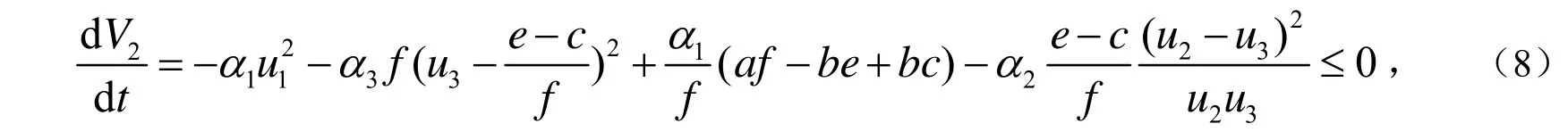
由Lyapunov-Lasalle不变原理知，当bc+af＜be ，1+2e＞c 时，平衡点全局渐近稳定.

令α2=eα3，bα1=dα3，当bc+af＞be ，e+ad＞c时，有：

由Lyapunov-Lasalle不变原理知，当bc+af＞be ，e+ad＞c时，平衡点全局渐近稳定.

2 系统（3）的稳定性

由偏微分方程基本理论可知，存在T＞0，使得问题（3）在[0,T）上存在唯一解.类似于文献[3]定理3.1的证明.可以证明如下定理：

定理2 设（u（x,t）,u（x,t）,u（x,t））∈[C（×[0,T））∩C2,1（×[1,T ））]3是u（x,0）=u≥123ii00（i=1,2,3）时问题（3）的解，其中[0,T）是解的最大存在区间，则存在依赖于Ω、问题（3）的系数及初值ui0（i=1,2,3）的正常数M，使得0≤ui（x,t）≤M（i =1,2,3），进一步，T=+∞.

为了分析平衡点的稳定性，需要引入一些概念和记号.设0＜μ1＜μ2＜μ3＜…是算子-Δ带有齐次Neumann边值条件的全体特征值，E（μi）是μi在C1（）中的特征空间，记X= {u∈[C1（]3|∂u =0on ∂Ω}，{φ：j =1,2,…,dimE（μ）}是E（μ）的标准正交基，并且记ηiji iX={c/c∈R3}，则有：ijφij

引理1[4]设a,b为正常数，φ,φ∈C1[a,∞），φ（t）≥0，φ有下界.如果φ'（t）≤-bφ （t ）且φ'（t）≤K（∀t≥a），K为正常数，则φ（t ）=0.

由定理2可知，系统（3）的解u1（x,t）,u2（x,t）,u3（x,t ）在中一致有界，即存在不依赖于t的正常数C＞0，使得

再由文献[5]知，

定理3 下面结论成立：

1）系统（3）的平衡点E0（0,0,0）无条件不稳定；

2）当1+c＞ad，c＞ad+e时，系统（3）的平衡点E1（a,0,0）全局渐近稳定；

3）当bc+af＜be ，1+2e＞c 时，系统（3）的平衡点全局渐近稳定；

4）当bc+af＞be ，e+ad＞c 时，系统（3）的唯一正常数平衡点全局渐近稳定.

证明：由于1）– 4）的证明方法类似，本文只给出4）的详细证明过程.首先证明其局部渐近稳定性.

记D=diag（d1,d2,d3），L=DΔ+Gu（u*），则系统（3）在u*处的线性化方程为：ut=Lu.对i≥1，Xi在算子L下是不变的，λ是L的特征值当且仅当它是矩阵-uiD+Gu（u*）的特征值，矩阵-uiD+Gu（u*）的特征方程为：λ3+A1λ2+B1λ+C1=0，其中，

1B1＞0，C1＞0，直接计算可得，这里，

显然，c1,c2,c3＞0.又由于故AB-C＞0.111

由Routh-Hurwitz准则可知，对∀i≥1，此方程的三个特征值λi,1,λi,2,λi,3均具有负实部.

下面证明存在正常数δ，对任意i≥1，有：

令λ=μiξ ，则有由于μi→∞（i →∞），因此有：

下面证明其全局渐近稳定性.

设（u1,u2,u3）是系统（3）的任一正解，定义如下Lyapunov函数：

即对∀t ≥0，有V3（t）≥0.由（3）式和（9）式及分部积分公式可得：

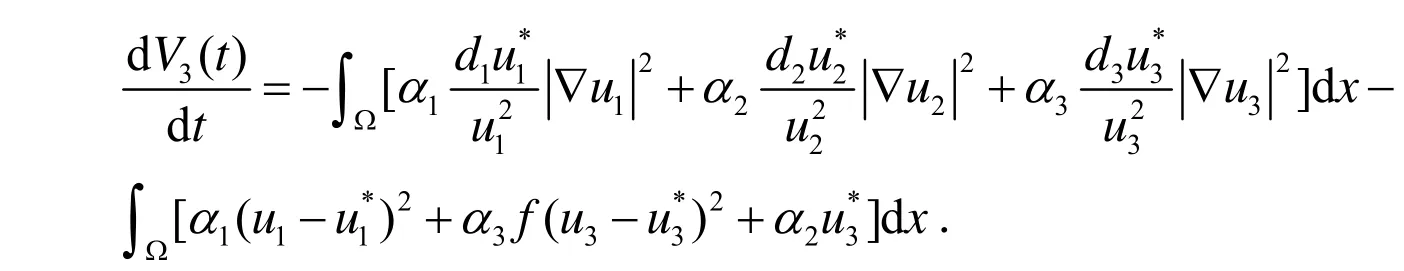
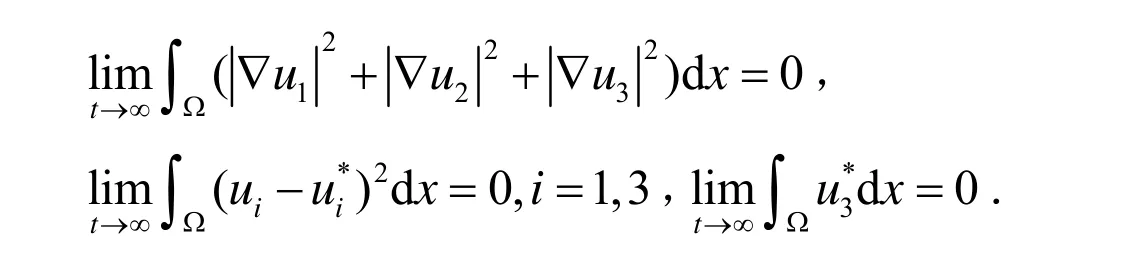
由（15）式和Poincare不等式可得：

由（12）式知，存在序列tm及非负函数wi∈C2（Ω），使得=0，i=1,2,3.结合（16）式和（17）式可知，wi≡（i=1,2,3），因此有：

结合（17）–（19）式及u*的局部稳定性可知u*全局渐近稳定.

同样可定义如下Lyapunov函数：

证明2）和3），证明方法与4）的完全相同，这里不再一一证明.

[1] Kar T K, Matsuda H.Permanence and optimization of harvesting return：a stage-structured prey-predator fishery [J].Journal of Environmental Sciences, 2007, 1：35-46.

[2] Lin Z G, Pedersen M.Stability in a diffusive food-chain model with michaelis-menten functional response [J].Nonlinear Analysis, 2004, 57：421-433.

[3] Zhang R, Guo L, Fu S M.Global behavior for a dcturiffusive predator-prey model with stage structure and nonlinear density restriction-I：The case inℝn[J].Boundary Value Problems, 2009, DOI：10.1155/2009/378363.

[4] Brown K J, Dume P C, Gardner R A.A similinear parabolic system arising in the theory of supercon ductivity [J].Journal of Differential Equations, 1981, 40：232-252.

[5] Henry D.Geometric theory of semilinear parabolic equations[M].New York：Springer, 1993, 91-99.

Stability of a Prey-predator Diffusion Model with Stage Structure

MIAO Liangying1, ZhANG Rui1, LIU Zhigao2, LU Xueli1
（1.School of Mathematics, Physics and Software Engineering, Lanzhou Jiaotong University, Lanzhou, China 730070；2.Baiyin Industry School, Baiyin, China 730900）

A prey-predator diffusion model with predator-stage structure is studied in this paper, and the locally asymptotical stability and the globally asymptotical stability of the non-negative constant steady states are given with linearization and Lyapunov functions.

Prey-predator Model；Stage Structure；Diffusion；Stability.

O175.26

A

1674-3563（2013）04-0056-06

10.3875/j.issn.1674-3563.2013.04.009 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2013-01-03

甘肃省自然科学基金（1107RJZA197）；甘肃省教育厅硕导项目（1104-11）

苗亮英（1987- ），女，甘肃永登人，硕士研究生，研究方向：偏微分方程及其应用