基于Beta分布的改进的一次可靠度法研究

徐志军， 张 博， 王 凯， 郑俊杰

(1.河南工业大学 土木建筑学院，河南 郑州 450001；2. 华中科技大学 土木工程与力学学院，湖北 武汉 430074 )

在可靠度理论中，一次可靠度方法被广泛应用于结构可靠度分析中。一次可靠度法的优点在于，对于同一工程实例，当功能函数发生变化时，利用一次可靠度方法计算出的可靠度指标不变。Kiureghian[1]利用一次可靠度理论提出了一种改进的二次可靠度方法。Juang[2]将一次可靠度方法应用于地震荷载下砂土液化可靠度研究，得出了地震荷载下可靠度指标变化规律。Huang[3]针对一次可靠度的不足，提出了一种改进的可靠度计算方法，并将该方法应用于岩石力学中。徐志军[4]利用一次可靠度理论研究了基桩在竖向和水平荷载下的可靠度优化设计方法。Xiang[5]利用一次可靠度方法提出了动荷载下结构的疲劳可靠度研究方法。Shinozuka[6], Ang[7], Madsen[8]和其他相关学者研究了一次可靠度方法。但以上研究将功能函数中的随机变量假设为正态分布或对数正态分布，并采用图1中的计算方法计算可靠度指标。当功能函数的非线性程度较高，或随机变量不服从正态分布和对数正态分布时，采用以上现有研究成果无法保证计算效率和计算精度。

图1 一次可靠度方法示意

为了解决以上问题，Zhao[9]研究了随机变量的取值范围，提出了一种通用的一次可靠度和二次可靠度方法。Low和Tang[10]利用Excel软件提出了面向对象算法的一次可靠度方法。Melchers[11], Zhao[12]和其他相关学者研究了改进的一次可靠度方法，取得了一些有意义的成果。但这些研究成果要么计算过程繁琐，要么可能因不收敛导致无法计算可靠度指标。

为了提高一次可靠度方法的计算精度和计算效率，本文利用Beta分布拟合功能函数中的随机变量概率分布。并采用蒙特卡洛模拟法比较了利用不同概率分布的一次可靠度计算精度。最后，利用实例分析给出了本文方法的有效性。

1 随机变量的概率分析

1.1 正态分布与对数正态分布

正态分布和对数正态分布是工程中常用的两种概率分布。设Z=(Z1,Z2,L,Zn)为一随机变量服从正态分布，均值和标准方差分别为μZ和σZ，则随机变量Z的概率密度函数为

-∞

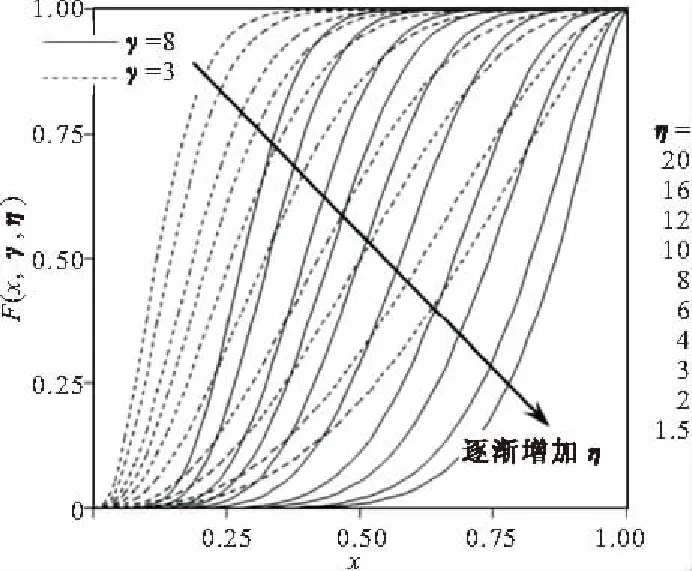
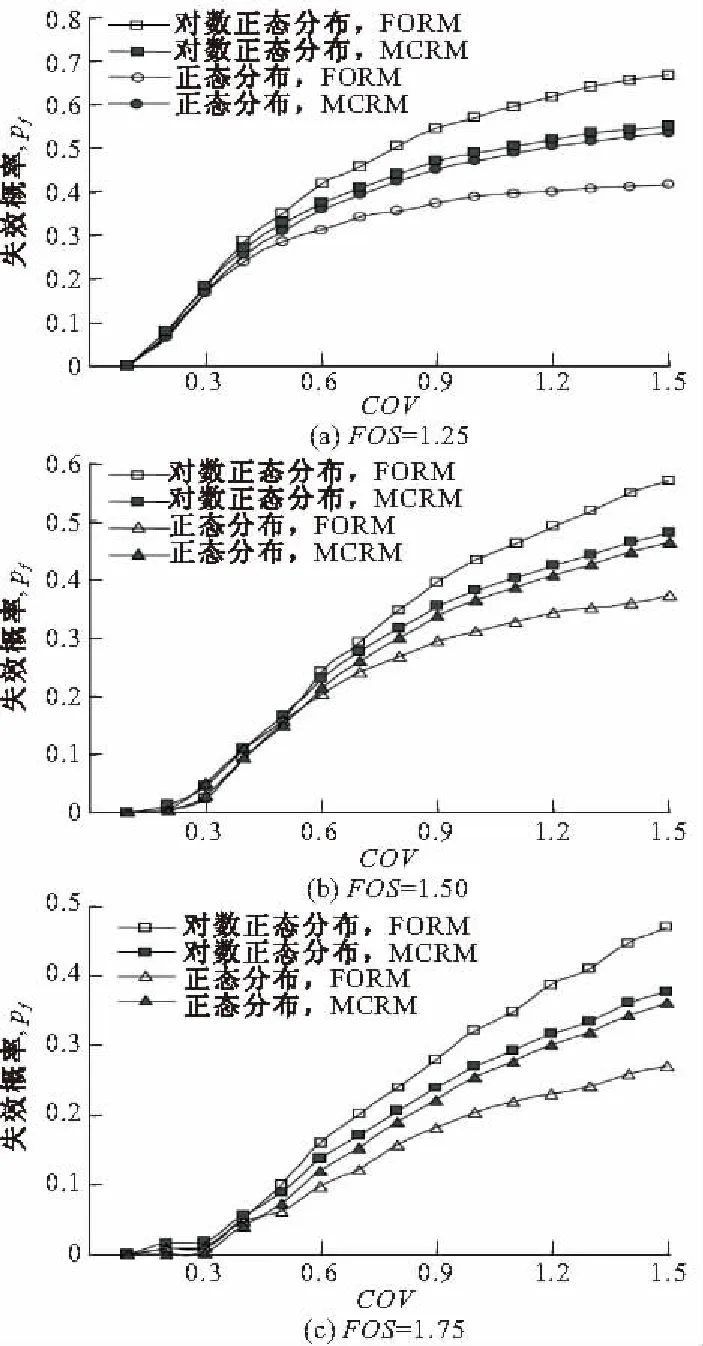
(1)

如果随机变量Z服从对数正态分布，则概率密度函数为

(2)

刘勇[13]通过详细研究每种概率分布的不足，介绍了Beta分布及各参数的确定方法，并通过实例分析验证了Beta分布拟合精度高于其他分布。

1.2 Beta分布

本文利用Beta分布拟合随机变量Z的概率分布。Beta分布的概率密度函数表达式为

fZ(Z)=

(3)

式中：Be(γ,η)为含有两个形参γ和η的Beta函数；m和n分别为随机变量的最小值和最大值。

令归一化变量为

(4)

则式(3)可转化为

(5)

式(5)是标准的Beta分布，其均值和方差分别为[7]

(6)

(7)

式中：μBe和varBe分别为fT(t)的均值和方差。根据式(6)和式(7)得，两个形参γ和η的计算公式分别为

(8)

(9)

对于不同的形参得出不同的曲线见图2～图5。由图2～图5可知，Beta分布能够接受大多数概率分布。刘勇通过详细的研究得出，Beta分布的拟合精度比常见的概率分布的拟合精度高。本文拟利用Beta分布拟合随机变量的概率分布。

图2 “凸”形Beta分布

图3 “凹”形Beta分布

图4 “凹”形Beta分布

图5 “凹”形Beta分布

2 一次可靠度法

在标准正态空间中，一次可靠度法就是在失效面中找到一个点，使这个点到原点之间的距离最短，这个最短距离就是可靠度指标(β)。其计算过程见图1，计算公式为

(10)

也可以用下面的计算公式

(11)

式中：μ为X的均值；C为协方差矩阵；R为相关系数矩阵；F为失效区域；μi为xi的均值；σi为xi的标准方差。式(10)实际上是个优化过程，具体的计算过程可采用Excel软件或Matlab编程完成。

在式(10)中，当Z服从正态分布时，二次型的(Z-μ)TC-1(Z-μ)是一个非正指数型多变量正态概率密度函数。Z服从其他概率分布的情况在第3部分详细给出。

3 实例分析

文献[3]给出了一个平面应变模型，平面的每个单位受力情况见图6。在图6中，σ3=1.0。由于受各种不确定因素的影响，排水强度参数即黏聚力和内摩擦角应视为一随机变量，两者的均值分布为μc=0.1和μtanφ=0.3。尽管两者的变异系数处于0.05到0.5之间，为了方便研究，两者的变异系数取

0

图6 单位单元的平面应变示意

利用摩尔库伦失效准则，可得如下公式

σ1f=σ3ftan2(45°+φ/2)+2ctan(45°+φ/2)

(12)

式中：c和φ分别为土的黏聚力和内摩擦角。

定义如下的安全系数

(13)

为了利用一次可靠度法计算平面应变的可靠度指标，将黏聚力c和φ内摩擦角视为随机变量，基于摩尔库伦失效准则，建立如下的极限状态方程

(14)

本文将基于式(14)讨论平面应变的可靠度指标。表1给出了不同轴向荷载下安全系数。基于表1中的数值，利用VBA语言得出式(10)的数组公式为

“=sqrt(mmult(transpose(nx),mmult (minverse(crmat);nx)))”

(15)

在本文中，将重点研究正态分布、对数正态分布和Beta分布的拟合精度。由概率理论可知，正态概率分布特性(均值和方差)转化为标准正态分布概率分布的特性计算公式为

(16)

μN=x-σNΦ-1[F(x)]

(17)

式中：x为原始的非正态变量；Φ-1[·]为标准正态分布的逆；F(x)和f(x)分别为x的概率分布函数和密度函数；φ{·}为标准概率分布的密度函数。

由式(16)和式(17)，利用VBA将对数正态分布变量和Beta分布变量转化为正态分布。

表1 不同安全系数下 σ1 的计算结果

为了对比计算精度，利用蒙特卡罗模拟法对比各种概率分布的计算结果。基于VBA语言，利用图1和图7计算出当c和tanφ分别服从正态分布和对数正态分布时平面应变的可靠度指标见图8。由图8可看出，当c和tanφ服从对数正态分布时利用一次可靠度计算结果高估了可靠度指标；当c和tanφ服从正态分布时，利用一次可靠度计算结果低估了可靠度指标。譬如，当安全系数FOS=1.25，变异系数COV=1.50时，当c和tanφ服从对数正态分布时，计算出的可靠度指标为0.671；当c和tanφ服从正态分布时，计算出的可靠度指标为0.417，两者之间的差值为0.254。在图7中，当COV=1.50时，利用两种概率分布计算出的可靠度指标之间的差值都在0.200以上，这在工程中是不容许的[7]。

为了提高计算精度，本文利用Beta分布拟合c和tanφ的概率分布。图8和图9分别给出了当c和tanφ服从对数正态分布和正态分布分别与Beta分布的对比计算结果。从图8和图9可看出，利用Beta分布的计算精度高于对数正态分布和正态分布。在图8和图9中，利用Beta分布和其他两种分布的计算结果之间的差值介于0.008～0.01之间。因此，本文提出的Beta分布拟合随机变量的概率不仅大大提高了计算精度，而且在保证迭代收敛的前提下提高了计算效率。

图 7 变量服从正态分布和对数正态分布时的计算结果

图 8 变量服从对数正态分布和Beta分布时的计算结果

图9 变量服从正态分布和Beta分布时的计算结果

4 结 论

利用常用的概率分布(对数正态分布和正态分布)拟合工程数据存在着拟合精度不高的问题。本文利用beta分布拟合工程数据的概率分布，并利用平面应变问题验证了本文方法的有效性，得到以下结论：

(1)当c和tanφ服从对数正态分布时利用一次可靠度计算结果高估了可靠度指标；当c和tanφ服从正态分布时，利用一次可靠度计算结果低估了可靠度指标。

(2)利用Beta分布的计算精度高于对数正态分布和正态分布。本文提出的Beta分布拟合随机变量的概率不仅大大提高了计算精度，而且在保证迭代收敛的前提下提高了计算效率。

[1] Kiureghian A D, Lin H Z, Hwang S J. Second-order reliability approximations[J]. Journal of Engineering Mechanics, 1987, 113(8): 1208-1225.

[2] Juang C H, Fang S Y, Khor E H. First-order reliability method for probabilistic liquefaction triggering analysis using CPT[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(3): 337-350.

[3] Huang J S, Griffiths D V. Observations on FORM in a simple geomechanics example[J]. Structural Safety, 2011, 33(1): 115-119.

[4] 徐志军. 基桩承载力可靠度分析及可靠度优化设计研究[D]. 武汉：华中科技大学，2012.

[5] Xiang Y B, Liu Y M. Inverse first-order reliability method for probabilistic fatigue life prediction of composite laminates under multiaxial loading[J]. Journal of Aerospace Engineering, 2011, 24(2): 189-198.

[6] Shinozuka M. Basic analysis of structural safety[J]. Journal of Structural Engineering, 1983, 109(3): 721-40.

[7] Ang H S, Tang W H. Probability Concepts in Engineering Planning and Design(4th Edition)[M]. New York: John Wiley, 2007.

[8] Madsen H O, Krenk S, Lind N C. Methods of Structural Safety[M]. Englewood Cliffs, NJ: Prentice-Hall, 1986.

[9] Zhao Y G, Ono T. A general procedure for first/second-order reliability method (FORM/SORM)[J]. Structural Safety, 1999, 21(2): 95-112.

[10] Low B K, Tang W H. Efficient spreadsheet algorithm for first-order reliability method[J]. Journal of Engineering Mechanics, 2007, 133(12): 1378-1387.

[11] Melchers R E. Structural Reliability Analysis and Prediction, 4nd Edition[M]. Chichester: John Wiley, 2006.

[12] Zhao Y G, Ono T. Moment methods for structural reliability[J]. Structural Safety, 2001, 23(1): 47-75.

[13] 刘 勇，郑俊杰，郭 嘉.分布的参数确定及其在岩土工程中的应用[J]. 岩土工程技术，2006，20(5)：240-244.