弱 Gorenstein FP-内射模

陈文静, 杨晓燕

（西北师范大学数学与统计学院,甘肃 兰州730070）

1 引言及预备知识

令R是具有单位元的结合环,所有涉及的模均是酉模.对任意的模M,用M+表示模M的示性模HomZ（M,Q/Z）.对未作解释的标记、事实和概念,参见文献［1-2］.

E.E.Enochs等［3］引入了 Gorenstein 平坦模的概念.E.E.Enochs等［4］在一般环上引入了Gorenstein投射模和Gorenstein内射模的概念.近年来,众多学者对Gorenstein投射模、Gorenstein内射模和Gorenstein平坦模进行了大量的研究,参见文献［5-9］.D.Bennis 等［10］引入了强 Gorenstein 投射模、强Gorenstein内射模和强Gorenstein平坦模的概念.他们证明了一个模是Gorenstein投射（内射）的当且仅当它是一个强Gorenstein投射（内射）模的直和项.

Z.H.Gao 等［11］引入了 Gorenstein FP-内射模的概念,利用Gorenstein FP-内射模对FP-自内射凝聚环进行了刻画.Z.H.Gao［12］引入了弱Gorenstein投射模、弱Gorenstein内射模和弱Gorenstein平坦模的概念,通过这些模类对QF环和FC环进行了刻画.同时引入了弱Gorenstein FP-内射模的概念,证明了在左凝聚环上如果M是弱Gorenstein FP-内射左R-模,那么M+是弱Gorenstein平坦右 R-模.Z.H.Gao［13］引入了强 Gorenstein FP-内射模的概念,通过强Gorenstein FP-内射模对FC环进行了刻画.

本文研究了弱Gorenstein FP-内射模,证明了凝聚环上弱Gorenstein FP-内射模是强Gorenstein FP-内射模的直和项,利用弱Gorenstein FP-内射模对FP-自内射环进行了刻画,讨论了凝聚环上FP-内射模类、Gorenstein FP-内射模类和弱Gorenstein FP-内射模类之间的联系.

首先回顾一些概念.称左R-模M是FP-内射（或绝对纯）的［14-15］,如果对任意有限表示左R-模P,.左R-模M的FP-内射维数FP-idR（M）定义为使得的最小的 n.环 R的左 FP-内射整体维数 l.FP-dim（R）定义为所有左R-模的FP-内射维数的上确界.称左R-模M是Gorenstein FP-内射模［11］,如果存在一个FP-内射左R-模的正合列

使得,并且对任意投射维数有限的有限表示左R-模P,HomR（P,E）是正合的.称左R-模M是强Gorenstein FP-内射模［13］,如果存在一个FP-内射左R-模的正合列

使得M≅Im（f）,并且对任意投射维数有限的有限表示左R-模P,HomR（P,E）是正合的.

2 弱Gorenstein FP-内射模

命题2.9设R是左凝聚环,并且每个内射左R-模有有限的平坦维数.如果M是弱Gorenstein FP-内射左R-模,那么M+是Gorenstein平坦右R-模.

证明由文献［11］的命题3.7和本文命题2.8,结论显然.

称R是n-FC环［17］,如果R是双边凝聚环且FP-idR（R）≤n,FP-id（R）R≤n.

推论2.10［12］设R是n-FC环.如果M是弱Gorenstein FP-内射左 R-模,那么M+是Gorenstein平坦右R-模.

推论2.11设R是 n-FC环.如果 M是Gorenstein FP-内射左 R-模,那么M+是Gorenstein平坦右R-模.

称左R-模M是强余纯平坦模［18］,如果对任意内射右R-模I及i≥1,

命题2.12设R是n-FC环,M是弱Gorenstein FP-内射左R-模,则以下等价:

1）M+是弱Gorenstein平坦右R-模；

2）M+是Gorenstein平坦右R-模；

3）M+是强余纯平坦右R-模；

4） （M+）+是Gorenstein内射左R-模.

证明由推论2.10,M+是Gorenstein平坦右R-模.因为R是n-FC环,所以由文献［12］的命题3.8 知,1）⇔2）⇔3）⇔4）.

命题得证.

定理2.13设R是任意环,则以下等价:

1）每个左R-模是弱Gorenstein FP-内射的；

2）每个投射左R-模是FP-内射的；

3）每个自由左R-模是FP-内射的；

4）环R是左FP-自内射的.

证明1）⇒2） 设P是投射左R-模.由1）,P是弱Gorenstein FP-内射左R-模.由命题2.3,存在短正合列,其中E是FP-内射左R-模,N是弱Gorenstein FP-内射左R-模.因为P是投射左R-模,所以短正合列0是可裂的.因此E≅N⊕P.又因为E是FP-内射左R-模,所以由文献［16］的引理2.1知,左R-模P是FP-内射的.

2）⇒1） 设M 是左 R-模,为M的一个内射分解,为M的一个投射分解.因为内射左R-模是FP-内射的,又由2）,每个投射左R

-模是FP-内射的,所以存在FP-内射左R-模的正合列

使得.因此 M 是弱 Gorenstein FP-内射的.

同理可证1）⇔3）.

3）⇔4） 设 F 是自由左R-模,则 F≅R（A）.由文献［16］的引理2.1,左R-模F是FP-内射的当且仅当左R-模R是FP-内射的.定理得证.

推论2.14设R是左凝聚环,则以下等价:

1）每个左R-模是弱Gorenstein FP-内射的；

2）每个左R-模是Gorenstein FP-内射的；

3）每个投射左R-模是FP-内射的；

4）每个自由左R-模是FP-内射的；

5）环R是左FP-自内射的.

证明由命题2.8和定理2.13,结论显然.

注2.15已知,有限表示平坦模类与有限表示投射模类是同一个类.由定理2.13知,投射的FP-模类与自由的FP-模类是同一个类.因此有限表示自由的FP-模类、有限表示投射的FP-模类和有限表示平坦的FP-模类是同一个类.

称左R-模M是Gorenstein内射模［3］,如果存在一个内射左R-模的正合列

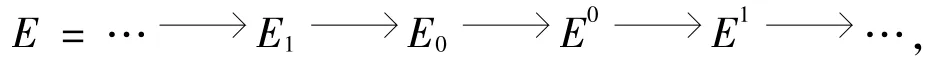
使得,并且对任意内射左R-模Q,HomR（Q,E）是正合的.Gorenstein投射左R-模的定义是对偶的.

命题2.16设R是双边凝聚环,则以下等价:

1）环R是左FP-自内射的；

2）每个弱Gorenstein FP-内射左R-模是Gorenstein平坦的；

3）每个Gorenstein内射左R-模是Gorenstein平坦的；

4）每个内射左R-模是Gorenstein平坦的；

5）每个Gorenstein投射左R-模是弱Gorenstein FP-内射的；

6）每个投射左R-模是弱Gorenstein FP-内射的；

7）每个Gorenstein平坦左R-模是弱Gorenstein FP-内射的；

8）每个平坦左R-模是弱Gorenstein FP-内射的；

9）环R是FC环.

以上1）～8）等价于右的情形.

证明因为R是双边凝聚环,所以由命题2.8知,弱Gorenstein FP-内射左R-模是Gorenstein FP-内射的.因此由文献［11］的定理3.6知,1）⇔2）⇔3）⇔4）⇔5）⇔6）⇔7）⇔8）.因为 R 是双边凝聚环,所以R是左和右FP-自内射的的当且仅当R是FC 环,所以1）⇔9）.

命题得证.

命题2.17FP-内射左R-模是弱Gorenstein FP-内射左R-模.反之,当R是左凝聚环且l.FP-dim（R）＜∞时,弱Gorenstein FP-内射左R-模是FP-内射左R-模.

证明由注2.2,只需证当R是左凝聚环且l.FP-dim（R）＜∞时,每个弱Gorenstein FP-内射左R-模是FP-内射左R-模.不失一般性,设l.FP-dim（R）＝m＜∞,下对m进行数学归纳.

1）若m＝0,则任意左R-模是FP-内射的,结论显然.

2）假设m≥1.设M是弱Gorenstein FP-内射左R-模.由命题2.3,存在一个左R-模的正合列,其中每个Ei是FP-内射左R-模.设,则有是正合的.因为FP-idR（L）≤m,R是左凝聚环,所以由文献［14］的引理3.1知,M是FP-内射左R-模.命题得证.

命题2.18设R是左凝聚环.如果l.FP-dim（R）＜∞,那么FP-内射模类,Gorenstein FP-内射模类,弱Gorenstein FP-内射模类是同一个类.

证明由命题2.8和命题2.17,结论显然.

［1］ Anderson F W,Fuller K R.Rings and Categories of Modules［M］.New York:Springer-Verlag,1992.

［2］ Rotman J J.An Introduction to Homological Algebra［M］.London:Academic Press,1979.

［3］Enochs E E,Jenda O M G,Torrecillas B.Gorenstein平坦模［J］.南京大学学报数学半年刊,1993,10（1）:1-9.

［4］ Enochs E E,Jenda O M G.Gorenstein injective and projective modules［J］.Math Zeit,1995,220（1）:611-633.

［5］ Mao L X,Ding N Q.Gorenstein FP-injective and Gorenstein flat modules［J］.J Algebra Appl,2008,7:491-506.

［6］ Bennis D.Rings over which the class of Gorenstein flat modules is closed under extensions［J］.Commun Algebra,2009,37:855-868.

［7］ Yang X Y,Liu Z K.Gorenstein projective,injective and flat modules［J］.J Aust Math Soc,2009,87:395-407.

［8］ Bennis D,Mahdou N.Global Gorenstein dimension［J］.Proc Am Math Soc,2010,138:461-465.

［9］ Yang X Y,Liu Z K.Strongly Gorenstein projective,injective and flat modules［J］.J Algebra,2008,320（7）:2659-2674.

［10］ Bennis D,Mahdou N.Strongly Gorenstein projective,injective and flat modules［J］.J Pure Appl Algebra,2007,7:491-506.

［11］ Gao Z H,Wang F G.Coherent rings and Gorenstein FP-injective modules［J］.Commun Algebra,2012,40:1669-1679.

［12］ Gao Z H.Weak Gorenstein projective,injective and flat modules［J］.J Algebra Appl,2013,12（2）:3841-3858.

［13］ Gao Z H.On strongly Gorenstein FP-injective modules［J］.Commun Algebra,2013,41:3035-3044.

［14］ Stenströ m B.Coherent rings and FP-injective modules［J］.J London Math Soc,1970,2:323-329.

［15］ Maddox B H.Absolutely pure modules［J］.Proc Am Math Soc,1967,18:155-158.

［16］ Jain S.Flat and FP-injectivity［J］.Proc Am Math Soc,1973,41:437-442.

［17］ Ding N Q,Chen J L.Coherent rings with finite self-FP-injective dimenson［J］.Commun Algebra,1996,24:2963-2980.

［18］ Enochs E E,Jenda O M G.Copure injective resolutions,flat resolvents and dimension［J］.Comment Math Univ Carolin,1993,34:203-211.