Sensitivity Analysis for a New System of Parametric Generalized Mixed Implicity Equilibrium Problems in Banach Spaces

DING Xieping

（College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan）

1 Introduction

In recent years,much attention has been devoted to developing general methods for the sensitivity analysis of solution set of various variational inclusions and equilibrium problems.From the mathematical and engineering points of view,sensitivity properties of various variational inclusions and equilibrium problems can provide new insight concerning the problem being studied and can stimulate ideas for solving these problems.The sensitivity analysis of solution set for various parametric variational inclusions have been studied extensively by many authors using quite different methods,see ［1-21］ and the references therein.It is worth mentioning that most of the results in the direction have been obtained in the setting of Hilbert spaces.

Recently,Kazmi and Khan［22］studied sensitivity analysis for parametric generalized implicit quasi-variational-like inclusions involving P-η-accretive mappings and Ding［23］studied sensitivity analysis for a system of parametric generalized implicit quasi-variational-like inclusions involving H-η-monotone mappings in uniformly smooth Banach spaces respectively.By using the Yosida approximation and Wiener-Hopf equation technique,Moudafi［24］and Huang et al［25］studied the sensitivity analysis of solutions for generalized mixed implicit equilibrium problems in Hilbert spaces.By using the technique of the system of auxiliary equation problems,Ding［26］studied sensitivity analysis for a system of generalized mixed implicity equilibrium problems in uniformly smooth Banach spaces.

Inspired and motivated by the above works,we shall introduce and study a new system of parametric generalized mixed implicit equilibrium problems involving non-monotone set-valued mappings in real Banach spaces.First,an auxiliary mixed equilibrium problem（AMEP） is introduced.The existence and uniqueness of solutions of the AMEP is proved under quite mild assumptions without any coercive conditions.Next,by using the solution mapping of the AMEP,a system of parametric generalized equation problems（SPGEP） is considered and its equivalence with the SPGMIEP is also proved.By using a fixed point formulation of the SPGEP,we study the behavior and sensitivity analysis of solution set of the SPGMIEP.Under suitable assumptions,we prove that the solution set of the SPGMIEP is nonempty,closed and Lipschitz continuous with respect to the parameters.Our results are new,which improve and generalize some known results in this field.

2 Preliminaries

Let B be a real Banach space with dual space B*and let‖·‖denote the norm of B and B*and〈· ,· 〉 denote the duality pairing between B*and B.Let R＝（-∞,+∞）and C（B）be the family of all nonempty compact subsets of B.

Definition 2.1Let C be a closed convex subset of a Hausdorff topological vector space E.A real valued bifunction F:C×C→（-∞,∞）is said to be

（i） monotone if

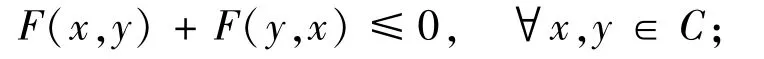
（ii） α-strongly monotone if there exists a real α＞0 such that

（iii） δ-Lipschitz continuous if there exists a real δ＞0 such that

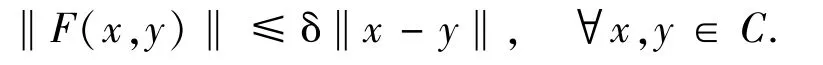
Remark 2.1Clearly,strong monotonicity of F implies monotonicity of F.

Definition 2.2A mapping η:B ×B→B*is said to be

（i）monotone if

（ii）δ-strongly monotone if there exists a δ ＞0 such that

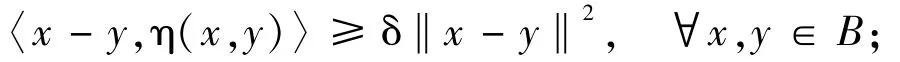
（iii） τ-Lipschitz continuous if there exists a constant τ＞0 such that

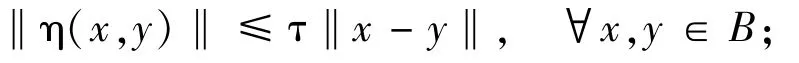
（iv） affine in first argument if

Definition 2.3The bifunction φ:B ×B→（-∞,+∞］is said to be skew-symmetric if

The skew-symmetric bifunctions have the properties which can be considered an analogue of monotonicity of gradient and nonnegativity of a second derivative for the convex function.For the properties and applications of the skew-symmetric bifunction,the reader may consult Antipin［27］.

The following result is a direct consequence of Theorem 1 of Ding and Tan［28］（also see Lemma 2.2 of Ding［29］）.

Lemma 2.1Let C be a nonempty convex subset of a topological vector space and let f:C×C→［-∞,+∞］be such that

（i） f（x,x）≥0 for each x∈C；

（ii） for each y∈C,x→f（x,y） is upper semicontinuous；

（iii） for each x∈C,y→f（x,y） is convex；

（iv） there exist a nonempty compact subset K of C and y∈K such that f（x,y） ＜0,∀x∈C＼K.

Then there exists a∈K such that f（,y）≥0 for all y∈C.

Lemma 2.2Let C be a closed convex subset of a reflexive Banach space B with intC≠Ø.Let F:C×C→R and φ:B ×B→R be two bifunctions, η:B ×B→B*be a mapping and ρ ＞0 be a positive number.Suppose the following conditions are satisfied:

（i） F is monotone and δ-Lipschitz continuous such that F（x,x）≥0 for each x∈C；

（ii） for each y∈C,x→F（x,y） is upper semicontinuous under weak topology and for each x∈C,y→F（x,y） is convex；

（iii） ηis σ-strongly monotone and τ-Lipschitz continuous with η（x,y） +η（y,x） ＝0,∀x,y∈B；

（iv） ηis affine in first argument and continuous from weak topology in B to weak*topology in B*in second argument；

（v） φis skew symmetric and weakly continuous,and φis proper convex in the first argument.

Then for each x∈B,the following auxiliary mixed equilibrium problem （AMEP）:find z∈C such that

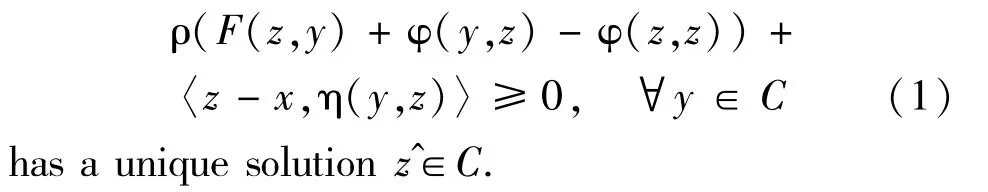
ProofFor each x∈B,define a bifunction f:C×C→R by

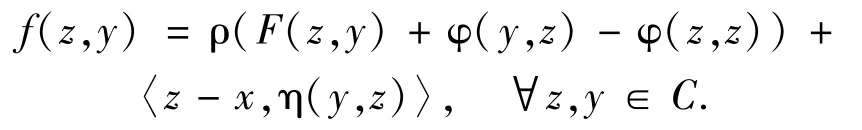
Since F（z,z）≥0 for each z∈C and η（x,y） +η（y,x） ＝0,∀x,y∈B,we have η（z,z） ＝0 for all z∈B,by the definition of f,we have that f（z,z）≥0,∀z∈C.The condition （i） of Lemma 2.1 is satisfied.Note that for each y∈C,x→F（x,y） is upper semicontinuous under weak topology,φis weakly continuous,and ηis continuous from weak topology in B to weak*topology in B*in second argument,we have for each y∈C,z→f（z,y） is weakly upper semicontinuous and so the condition （ii） of Lemma 2.2 is satisfied.Since for each z∈C,y→F（z,y） is convex and φis convex in first argument,and ηis affine in first argument,we have that for each z∈C,y→f（z,y） is convex.The condition （iii） of Lemma 2.1 is satisfied.By （v）,for each y∈C,z→φ（z,y） is proper convex,weakly continuous and int｛y∈C:φ（y,y） ＜∞｝ ＝intC≠Ø.Take y*∈int｛y∈C:φ（y,y） ＜∞｝.By Proposition I.2.6 of Pascali and Sburlan［30］, φ（· ,y*） is subdifferential at y*.Hence,we have

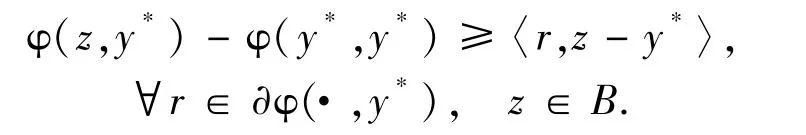
Noting that φ（·,· ） is skew symmetric,we have

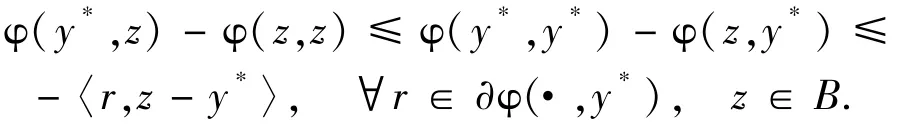
Since F is δ-Lipschitz continuous,and ηis σ-strongly monotone and τ-Lipschitz continuous,we have

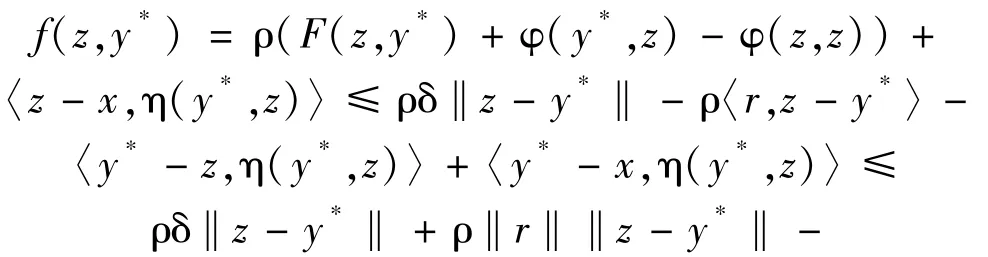
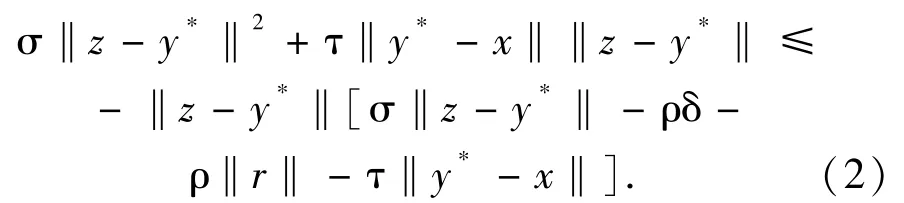
Let R ＝［ρ（δ+‖r‖） +τ‖y*-x‖］/σand K ＝｛z∈C:‖z-y*‖≤R｝.Then K is a weakly compact convex subset in C and y*∈K.It follows from （2）that f（z,y*） ＜0 for all z∈C＼K and hence the condition （iv） of Lemma 2.1 is satisfied.For each x∈B,by Lemma 2.1,there exists a point∈C such that f（,y）≥0,∀y∈C.By the definition of f,we obtain that for each x∈B,

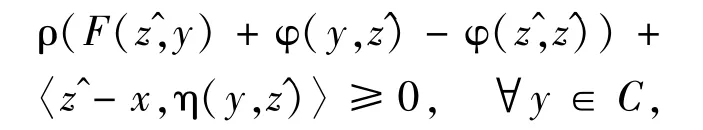
i.e.,∈C is a solution of the AMEP（1）.Now,we prove the uniqueness of solutions of the AMEP （1）.For each x∈B,let z1,z2∈C be any two solutions of the AMEP,then from the condition （i） we have

Noting η（z1,z2）+η（z2,z1） ＝0,taking y＝z2in （3）and y＝z1in（4） and adding these two inequalities,we obtain

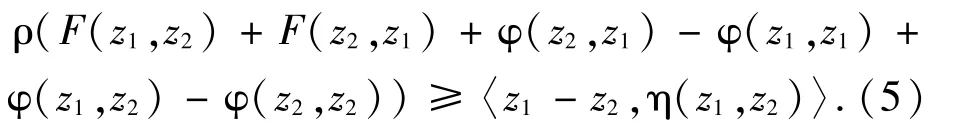
Assume z1≠z2.Noting that F is monotone,φis skew symmetric and ηis σ-strongly monotone,it follows from （5） that

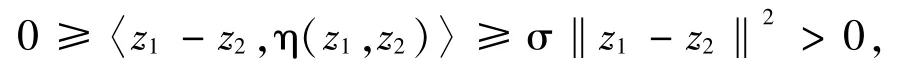
which is a contraction.Therefore,we must have z1＝z2.This completes the proof.

Remark 2.21）Lemma 2.2 improves Lemma 2.2 of Ding and Ho［21］in the following way:the coercive conditions of Lemma 2.2 in ［21］ is removed.

2）By Lemma 2.2,we also obtain that for each x∈B,there exists a uniquesuch that

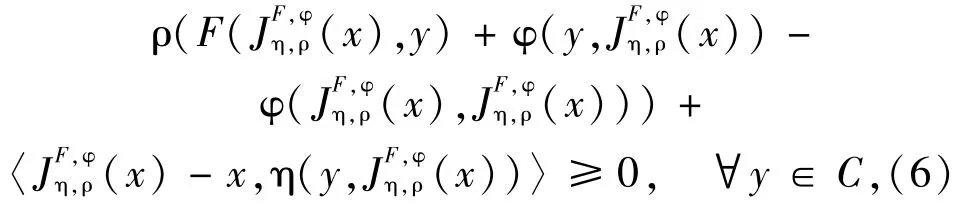
and hence the solution mapping:X → C of the AMEP （1） is a well-defined single-valued mapping.

Theorem 2.1In the assumptions of Lemma 2.2,if further assume that F is θ-strongly monotone,then the solution mapping:X →C of the AMEP

（1） is τ/（σ+ρθ）-Lipschitz continuous.

Remark 2.3Theorems 2.1 improves and generalizes Theorem 3.1 of Kazmi and Khan［31］and Theorem 2.1 of Ding and Ho［21］in following way:

1）from Hilbert spaces to reflexive Banach spaces；

2） the AMEP （1） is more general than the models in ［21,31-33］；

3）the coercive conditions is removed.

3 System of parametric generalized mixed implicit equilibrium problems

In what follows,unless other specified,let R＝（ -∞,+∞）.For each i∈｛1,2｝,let Bibe a real reflexive Banach space with norm‖·‖iand the dual spacebe the dual pair betweenand Bi, Λiand Ωibe two open subsets of Biin which parameters λiand ωitakes the values,C（Bi） denotes the family of all nonempty compact subsets of Bi,and（· ,· ） be the Hausdorff metric on C（Bi） defined by

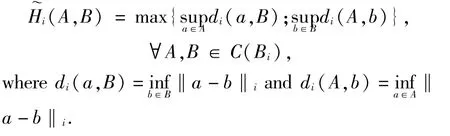
For each i∈｛1,2｝,let Cibe a nonempty closed convex subset of Biwith intCi≠Ø,Fi:Ci×Ci×Λi→R and φi:Ci×Ci→R be functions.For each i∈｛1,2｝,let gi:Ci×Λi→Ciwith gi（Ci,λi） ＝Ci,∀λi∈Λi, ηi:Bi×Bi×Ωi→and Mi:C1×C2×B1×B2×Ω1×Ω2→Bibe single-valued mappings,and Ti:C1×Ω1→C（B1） and Si:C2×Ω2→C（B2） be set-valued mappings.

We consider the following system of parametric generalized mixed implicit equilibrium problems（SPGMIEP）:for i∈｛1,2｝ and given （λi,ωi）∈Λi×Ωi,find （x1,x2）∈C1×C2, （u1,v1）∈T1（x1,ω1）×S1（x2,ω2）, （u2,v2）∈T2（x1,ω1） ×S2（x2,ω2）such that

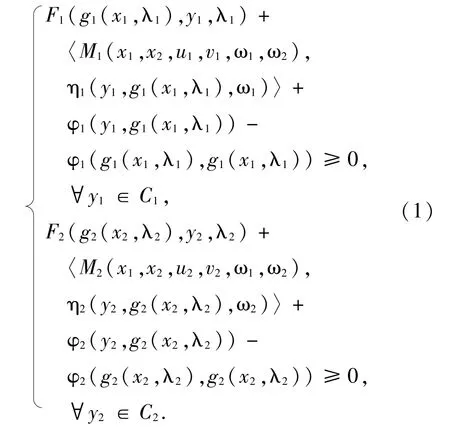
Special cases:

（I） If for i∈｛1,2｝,Let M1（x1,x2,u1,v1,ω1,ω2） ＝G1（x1,x2,ω1） +N1（u1,v1,ω1）and M2（x1,x2,u2,v2,ω1,ω2） ＝G2（x1,x2,ω2） +N2（u2,v2,ω2）,where Gi:C1×C2×Ωi→Biand Ni:B1×B2×Ωi→Biand φi≡0,then the SPGMIEP （1） reduces to the following parametric problem:for given （λi,ωi）∈Λi×Ωi,find （x1,x2）∈C1×C2, （u1,v1）∈T1（x1,ω1） ×S1（x2,ω2）, （u2,v2）∈T2（x1,ω1） ×S2（x2,ω2） such that

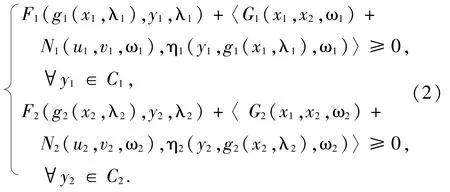
（II） If for i∈｛1,2｝,let Bi＝B,Ci＝C, Λi＝Λ, Ωi＝Ω,Fi＝F,Mi＝M,Ti＝T,Si＝S, ηi＝η,gi＝g and φi＝φ,then the SPGMIEP （1） reduces to the following parametric problem:for given （λ,ω）∈Λ×Ω,find x∈C, （u,v）∈T（x,ω） ×S（x,ω） such that

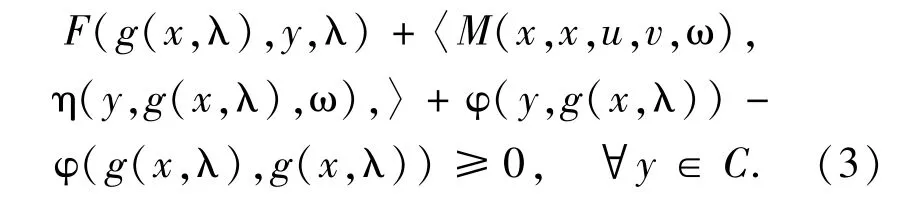
The problems（2） and （3） include many（parametric）generalized mixed equilibrium problems as special cases,for examples,see ［21-26,31-33］and the references therein.

Now,for i∈｛1,2｝ and fixed （λi,ωi）∈Λi×Ωi,we assume that Fi（· ,· ,λi）, η（· ,· ,ωi）and φisatisfy all conditions of Lemma 2.2.Related to SPGMIEP （1）,we consider the following system of parametric equation problems （SPEP）:find （x1,x2）∈C1×C2, （u1,v1）∈T1（x1,ω1） ×S1（x2,ω2）,（u2,v2）∈T2（x1,ω1） ×S2（x2,ω2）,such that

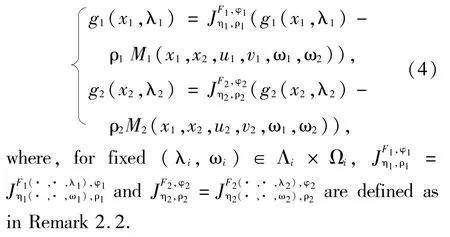
Lemma 3.1For fixed （λi,ωi）∈Λi×Ωi,（x1,x2,u1,v1,u2,v2） with （x1,x2）∈C1×C2, （u1,v1）∈T1（x1,ω1） ×S1（x2,ω2）, （u2,v2）∈T2（x1,ω1）×S2（x2,ω2） is a solution of the SPEP （4） if and only if（x1,x2,u1,v1,u2,v2） with （x1,x2）∈C1×C2, （u1,v1）∈T1（x1,ω1） ×S1（x2,ω2）, （u2,v2）∈T2（x1,ω1）×S2（x2,ω2） is a solution of the SGMIEP （1）.

ProofFor fixed （λi,ωi）∈Λi×Ωi,if（x1,x2,u1,v1,u2,v2）with （x1,x2）∈C1×C2, （u1,v1）∈T1（x1,ω1） ×S1（x2,ω2）, （u2,v2）∈T2（x1,ω1） ×S2（x2,ω2） is a solution of the SPEP （4）,then we have

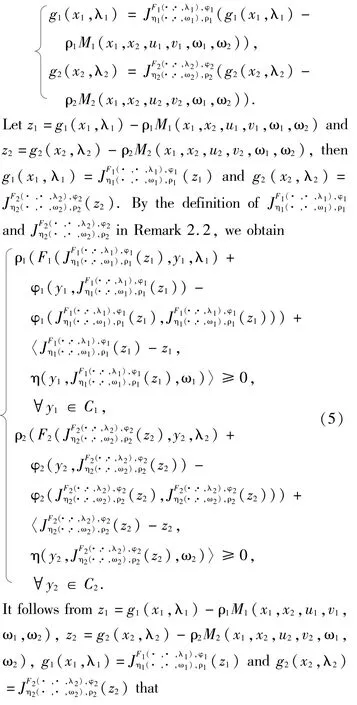
Hence （x1,x2,u1,v1,u2,v2） with （x1,x2）∈C1×C2,（u1,v1）∈T1（x1） ×S1（x2）, （u2,v2）∈T2（x1） ×S2（x2） is a solution of the SGMIEP （1）.

Conversely,for fixed （λi,ωi）∈Λi×Ωi,if（x1,x2,u1,v1,u2,v2） with （x1,x2）∈C1×C2, （u1,v1）∈T1（x1,ω1） ×S1（x2,ω2）, （u2,v2）∈T2（x1,ω1） ×S2（x2,ω2） is a solution of the SGMIEP （1）,then the system of inequalities （6） holds.For ρ1,ρ2＞0,it follows from （6） that

Let z1＝g1（x1,λ1） -ρ1M1（x1,x2,u1,v1,ω1）∈B1and z2＝g2（x2,λ2） -ρ2M2（x1,x2,u2,v2,ω2）∈B2,then we have

Remark 3.1Lemma 3.1 improves Lemma 3.1 of Ding and Ho［21］and generalizes Lemma 2.3 of Huang et al［25］and Lemma 3.1 of Kazmi and Khan［31］in the following ways:

1）from Hilbert spaces to Reflexive Banach spaces；

2）from a generalized mixed equilibrium problem to the more general system of generalized mixed implicit equilibrium problems.

Now,by Lemma 3.1,for each i∈｛1,2｝ and given （λi,ωi）∈Λi×Ωi,we can define the solution set S（λ1,λ2,ω1,ω2） of the SPGMIEP （1） as follows:

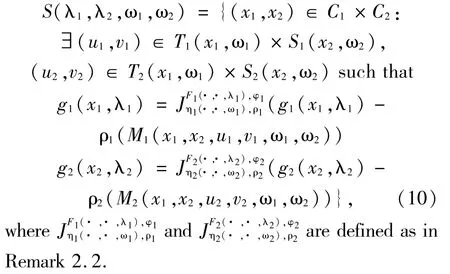
For i∈｛1,2｝,we define the mappings Φ1:C1×C2×Λ1×Ω1×Ω2→2C1and Φ2:C1×C2×Λ2×Ω1×Ω2→2C2as follows:

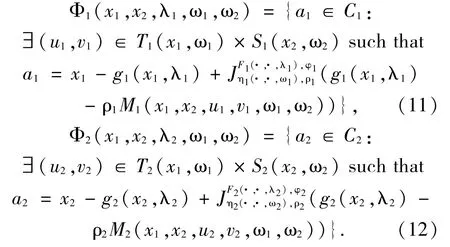
Again define a mapping Ψ:C1×C2×Λ1×Λ2×Ω1×Ω2→2B1×B2as follows:

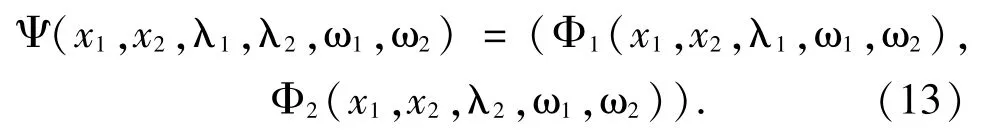
Lemma 3.2For i∈｛1,2｝ and given （λi,ωi）∈Λi×Ωi, （x1,x2） is a fixed point of Ψif and only if（x1,x2）∈S（λ1,λ2,ω1,ω2）,i.e,there exist（u1,v1）∈T1（x1,ω1） ×S1（x2,ω2）, （u2,v2）∈T2（x1,ω1） ×S2（x2,ω2） such that（x1,x2,u1,u2,v1,v2） is a solution of the SPGMIEP （1）.

ProofFor each fixed （λi,ωi）∈Λi×Ωi,by the definition of Ψ, （x1,x2）∈C1×C2is a fixed point of Ψif and only if there exist（u1,v1）∈T1（x1,ω1） ×S1（x2,ω2） and （u2,v2）∈T2（x1,ω1） ×S2（x2,ω2）such that

By Lemma 3.1,the relation （14） holds if and only if（x1,x2,u1,u2,v1,v2）is a solution of the SPGMIEP（1）.This completes the proof.

Definition 3.1For i＝1,2,Mi:C1×C2×B1×B2×Ω1×Ω2→Biis said to be （m（i,1）,m（i,2）,m（i,3）,m（i,4）,m（i,5）,m（i,6））-mixed Lipschitz continuous in first to six arguments,if there exist constants m（i,1）,m（i,2）,m（i,3）,m（i,4）,m（i,5）,m（i,6）＞0 such that

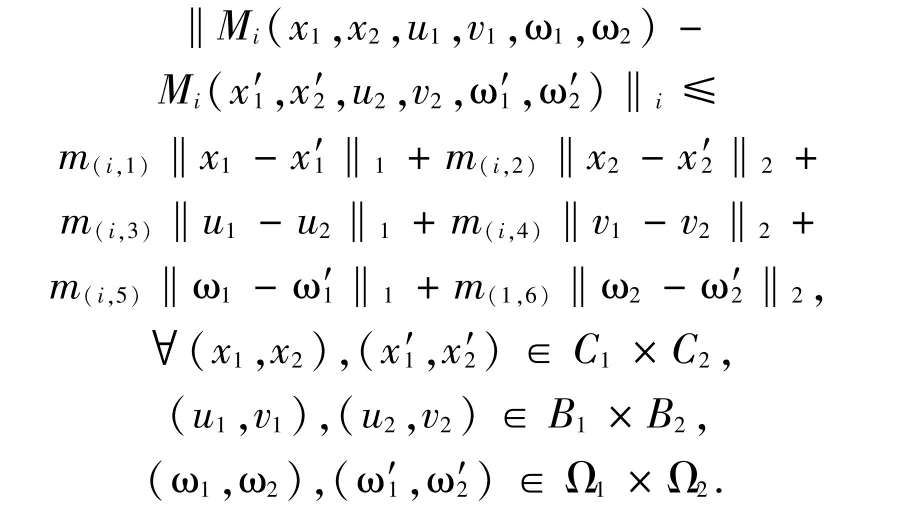
Definition 3.2For i∈｛1,2｝,let Ti:B1×Ω1→C（B1） be a set-valued mapping.

（i） Tiis said to be-μi-Lipschitz continuous in first argument,if there exists a constant μi＞0 such that

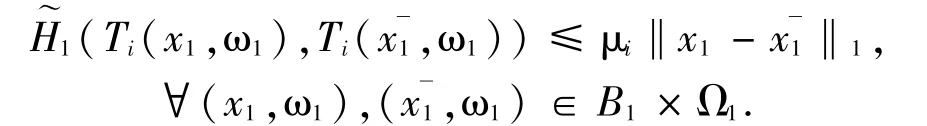
（ii） Tiis said to be-ti-Lipschitz continuous in second argument,if there exists a constant ti＞0 such that

Similarly,we can define the Lipschitz continuity of the mappings Si:C2×Ω2→C（B2）.

The modulus of smoothness of a Banach space B is the function ρB:［0,∞）→［0,∞） defined by

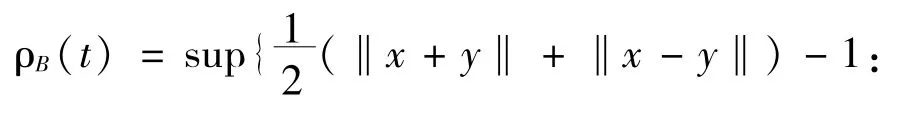
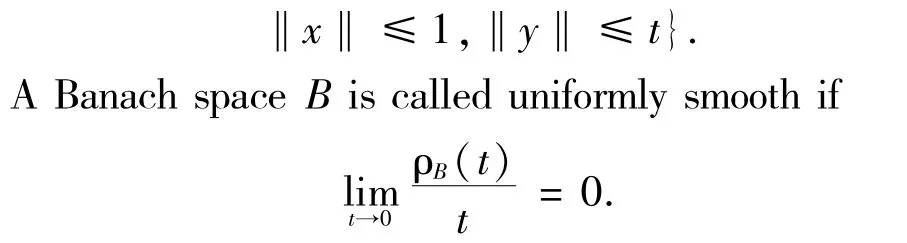
Definition 3.3Let K be a closed convex subset of a Banach space B.A mapping g:K→K is said to be γ-strongly accretive if,for any x,y∈K,there exist j（x-y）∈J（x-y） and a constant γ＞0 such that

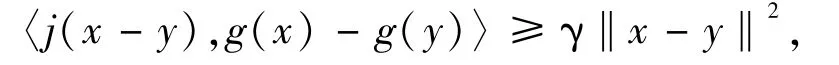
where J:B→2B*is the normalized duality mapping defined by

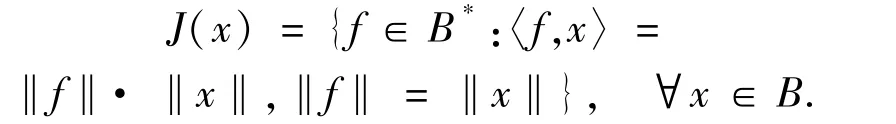
Lemma 3.3［34］Let B be a uniformly smooth Banach space and J be the normalized duality mapping from B into B*.Then,for all x,y∈B,we have

Lemma 3.4［35］Let（X,d） be a complete metric space and T1,T2:X→C（X） be two set-valued contractive mappings with same contractive constants θ∈（0,1）,i.e.,

Theorem 3.1For each i∈｛1,2｝,let Cibe a nonempty closed convex subset of a uniformly smooth Banach space Biwith ρBi（t）≤Dit2for some Di＞0.For fixed （λi,ωi）∈Λi×Ωi,Fi:Ci×Ci×Λi→R,ηi:Bi×Bi×Ωi→Biand φi:Ci×Ci→R satisfy all conditions of Theorem 2.1 where F, θ, δ, η, τ, σ and φare replaced by Fi, θi, δi, ηi, τi, σiand φi.Let Mi:C1×C2×B1×B2×Ω1×Ω2→Bibe（m（i,1）,m（i,2）,m（i,3）,m（i,4））-mixed Lipschitz continuous in first to fourth arguments,Ti:B1×Ω1→C（B1） be-μi-Lipschitz continuous in first argument,Si:B2×Ω2→CB（B2） be-si-Lipschitz continuous in first argument and gi:Ki×Λi→Kibe γi-strongly accretive and βi-lipschitz continuous in first argument.If the following conditions hold for ρ1,ρ2＞0:

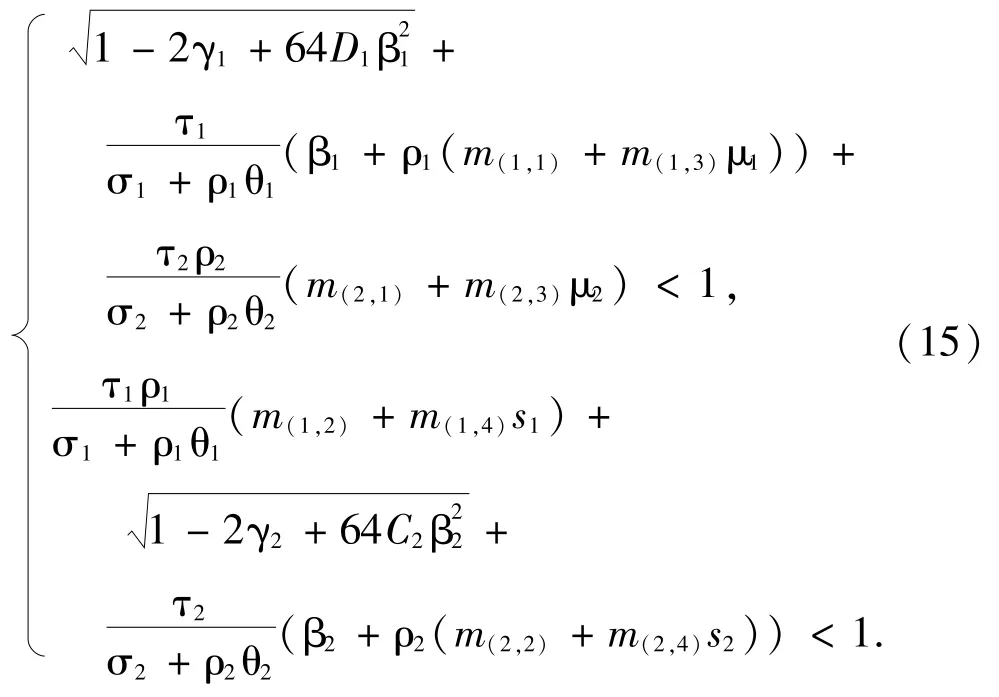
Then for any （x1,x2,λ1,λ2,ω1,ω2）∈C1×C2×Λ1×Λ2×Ω1×Ω2, Ψ（x1,x2,λ1,λ2,ω1,ω2）∈C（B1×B2） and Ψis a uniform*-contraction mapping with respect to （λi,ωi）∈Λi×Ωi,i＝1,2,where*is a Hausdorff metric on C（B1×B2）.Moreover,for each fixed （λi,ωi）∈Λi×Ωi,i＝1,2,the solution set S（λ1,λ2,ω1,ω2） of the SPGMIEP （1） is nonempty closed.

ProofLet（x1,x2,λ1,λ2,ω1,ω2） be an arbitrary element in C1×C2×Λ1×Λ2×Ω1×Ω2.Since for i＝1,2,Tiand Siare all compact-valued,and,giand Miare all continuous.By the definitions of Φ1and Φ2,we have Φ1（x1,x2,λ1,ω1,ω2）∈C（B1） and Φ2（x1,x2,λ2,ω1,ω2）∈C（B2）and hence Ψ（x1,x2,λ1,λ2,ω1,ω2）∈C（B1×B2）.For any fixed（x1,x2,λ1,λ2,ω1,ω2）,（1,2,λ1,λ2,ω1,ω2）∈C1×C2×Λ1×Λ2×Ω1×Ω2and for each（a1,a2）∈Ψ（x1,x2,λ1,λ2,ω1,ω2）,by definitions of Ψ and Φi,i∈｛1,2｝,we have that there exist（u1,v1）∈T1（x1,ω1） ×S1（x2,ω2） and （u2,v2）∈T2（x1,ω1） ×S2（x2,ω2） such that

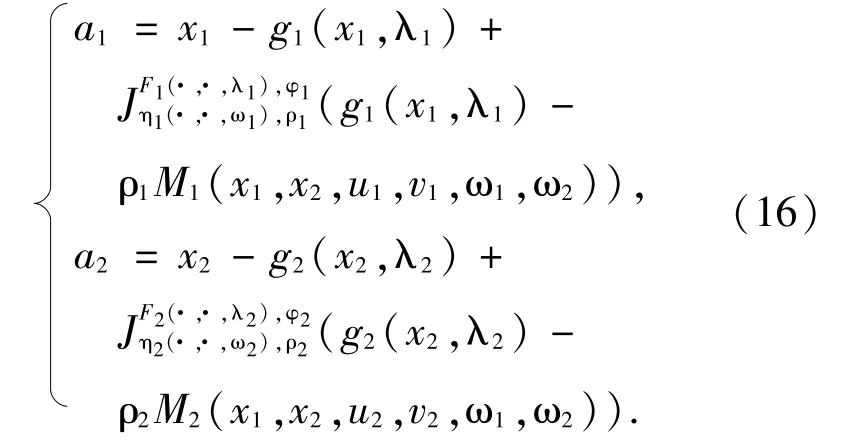
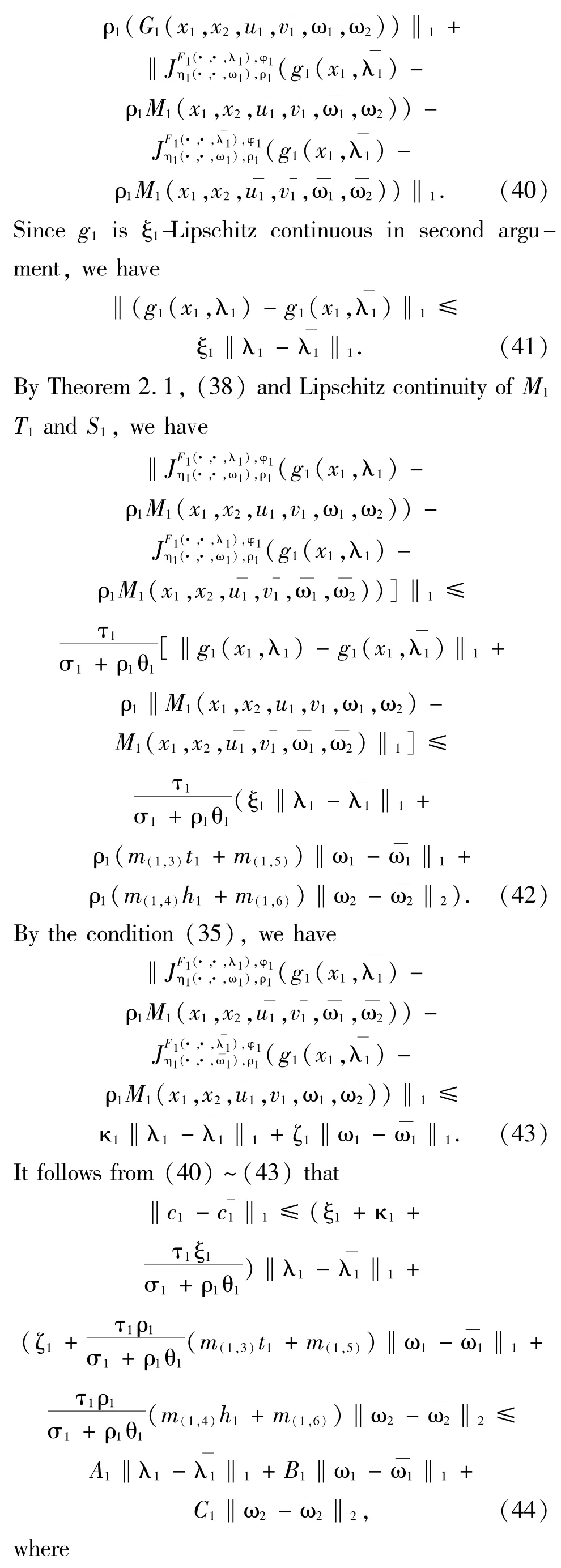
This shows that the solution set S（λ1,λ2,ω1,ω2）） of the SPGIQVLI（1） is a*-Lipschitz continuous mapping from Λ1×Λ2×Ω1×Ω2into B1×B2.This completes the proof.

［1］ Dafermos S.Sensitivity analysis in variational inequalities［J］.Math Oper Res,1988,13:421-434.

［2］ Mukherjee R N,Verma H L.Sensitivity analysis of generalized variational inequalities［J］.J Math Anal Appl,1992,167:299-304.

［3］ Noor M A.Sensitivity analysis for quasi-variational inequalities［J］.J Optim Theory Appl,1997,95:399-407.

［4］ Yen N D.Lipschitz continuity of solutions of variational inequalities with a parametric polyhedral constraint ［J］.Math Oper Res,1995,20:695-708.

［5］ Verma R U.Sensitivity analysis for generalized strongly monotone variational inclusions based on the （A,η）-resolvent operator technique［J］.Appl Math Lett,2006,19:1409-1413.

［6］ Robinson S M.Sensitivity analysis for variational inequalities by normal-map technique［C］//Giannessi F,Maugeri A.Variational Inequalities and Network Equilibrium Problems.New York:Plenum Press,1995.

［7］ Adly S.Perturbed algorithms and sensitivity analysis for a general class of variational inclusions ［J］.J Math Anal Appl,1996,201:609-630.

［8］ Noor M A,Noor K I.Sensitivity analysis for quasi-variational inclusions［J］.J Math Anal Appl,1999,236:290-299.

［9］ Agarwal R P,Cho Y J,Huang N J.Sensitivity analysis for strongly nonlinear quasi-variational inclusions［J］.Appl Math Lett,2000,13（6）:19-24.

［10］ Ding X P,Lou C L.On parametric generalized quasivariational inequalities［J］.J Optim Theory Appl,1999,100（1）:195-205.

［11］ Liu Z,Debnath L,Kang S M,et al.Sensitivity analysis for parametric completely generalized nonlinear implicit quasivariational inclusions［J］.J Math Anal Appl,2003,277:142-154.

［12］ Salahuddin.Parametric generalized set-valued variational inclusions and resolvent equations［J］.J Math Anal Appl,2004,198:146-156.

［13］ Park J Y,Jeong J U.Parametric generalized mixed variational inequalities［J］.Appl Math Lett,2004,17:43-48.

［14］ Ding X P.Sensitivity analysis for generalized nonlinear implicit quasi-variational inclusions［J］.Appl Math Lett,2004,17:225-235.

［15］ Ding X P.Sensitivity analysis of solution set for a new class of generalized implicit quasi-variational inclusions［J］.Fixed Point Theory and Applications,2006,7:81-94.

［16］ Ding X P.Parametric completely generalized nonlinear implicit quasi-variational inclusions involving h-maximal monotone mappings［J］.J Comput Appl Math,2005,182（2）:252-289.

［17］ Peng J W,Long X L.Sensitivity analysis for parametric completely generalized strongly nonlinear implicit quasi-variational inclusions［J］.Comput Math Appl,2005,50:869-880.

［18］ Agarwal R P,Huang N J,Tan M Y.Sensitivity analysis for a new system of generalized nonlinear mixed quasi-variational inclusions［J］.Appl Math Lett,2004,17:345-352.

［19］ Ding X P,Yao J C.Sensitivity analysis for a system of parametric mixed quasi-variational inclusions［J］.J Nonlinear Convex A-nal,2007,8（2）:211-225.

［20］ Ding X P,Wang Z B.Sensitivity analysis for a system of parametric generalized mixed quasi-variational inclusions involving （K,η）-monotone mappings［J］.Appl Math Comput,2009,214:318-327.

［21］ Ding X P,Ho J L.New Iterative algorithm for solving a system of generalized mixed implicit equilibrium problems in Banach spaces［J］.Taiwan J Math.2011,15（2）:673-695.

［22］Kazmi K R,Khan E A.Sensitivity analysis for parametric generalized implicit quasi-variational-like inclusions involving P-η-accretive mappings［J］.J Math Anal Appl.2008,337:1198-1211.

［23］ Ding X P.System of parametric generalized implicit quasi-variational-like inclusions involving H-η-monotone operators in Banach spaces［J］.J Sichuan Normal Univ:Natural Sci,2010,33（6）:1-11.

［24］ Moudafi A.Mixed equilibrium problems:sensitivity analysis and algorithmic aspects［J］.Comput Math Appl,2002,44:1099-1108.

［25］Huang N J,Lan H Y,Cho Y J.Sensitivity analysis for nonlinear generalized mixed implicit equilibrium problems with non-monotone set-valued mappings［J］.J Comput Appl Math,2006,196:608-618.

［26］Ding X P.Sensitivity analysis for a system of generalized mixed implicit equilibrium problems in uniformly smooth Banach spaces［J］.Nonlinear Anal,2010,73:1264-1276.

［27］ Antipin A S.Iterative gradient prediction-type methods for computing fixed-point of extremal mappings［C］//Guddat J,Jonden H Th,Nizicka F,et al.Parametric Optimization and Related Topics IV.Frankfurt Main:Peter Lang,1997:11-24.

［28］ Ding X P,Tan K K.A minimax inequality with applications to existence of equilibrium point and fixed point theorems ［J］.Colloq Math,1992,63:233-247.

［29］ Ding X P.Existence and algorithm of solutions for mixed equilibrium problems and bilevel mixed equilibrium problems in Banach spaces［J］.Acta Math Sinica,2012,28（3）:503-514.

［30］ Pascali D,Surian S.Nonlinear Mappings of Monotone Type［M］.Alphen aan den Rijn:Sijthoff and Noordhoff International Publishers,1978.

［31］ Kazmi K R,Khan F A.Existence and iterative approximation of solutions of generalized mixed equilibrium problems ［J］.Comput Math Appl,2008,56:1314-1321.

［32］ Ding X P.Existence and algorithm of solutions for a system of generalized mixed implicit equilibrium problems in Banach spaces［J］.Appl Math Mech,2010,31（9）:1049-1062.

［33］ Ding X P.Auxiliary principle and approximation solvability for system of new generalized mixed equilibrium problems in reflexive Banach spaces［J］.Appl Math Mech,2011,32（2）:231-240.

［34］Petryshyn W V.A characterization of strictly convexity of Banach spaces and other uses of duality mappings ［J］.J Funct Anal,1970,6:282-291.

［35］ Lim T C.On fixed point stability for set-valued contractive mappings with application to generalized differential equations ［J］.J Math Anal Appl,1985,110:436-441.

［36］ Nadler S B.Multivalued contraction mapping［J］.Pacific J Math,1969,30:475-488.