非线性动力系统极限环Runge-Kutta法求解的1个注记

黄文恺， 浣　石

( 广州大学土木工程学院， 广州 510006)



非线性动力系统极限环Runge-Kutta法求解的1个注记

黄文恺， 浣石*

( 广州大学土木工程学院， 广州 510006)

采用Matlab软件研究了Runge-Kutta直接积分法在计算非线性动力系统极限时存在的一个问题：单周期解误判为双周期或三周期. 直接调用Matlab自带程序ode45，并设定算法的相对误差. 以二元机翼强非线性颤振系统为例，研究发现，采用程序默认的相对误差来控制计算精度时，单周期极限环解出现了双周期和三周期；若修改相对误差的设定值则可提高控制精度，进而得到正确的解. 因此，在用Runge-Kutta法自带ode45程序计算非线性动力系统极限环时，应特别注意对计算精度的设置.

Runge-Kutta法； 非线性动力系统； 极限环； 相对误差

非定常气动力条件下的二元机翼非线性颤振模型是近几年来气动弹性力学研究最为广泛的模型之一，是一类非常复杂的非线性微分动力系统[1-10]. 该模型采用了不可压缩非定常气动力模型，使复杂的非线性颤振分析更加困难，其研究方法以数值方法和谐波平衡法为主[1]. 数值方法是最常用的方法，具有很高的精度，常用于验证其它方法的有效性和合理性. 然而，数值方法本身也存在问题，比如无法求解不稳定的解，1次只能求解1个解的限制等.

极限环振动是非线性颤振系统的一种典型动力响应[11-14]. 数值模拟是求解极限环的主要手段. 一般地，极限环解很难采用解析方法求解. 而且，即使采用解析或半解析方法求解，其结果也需要采用数值模拟验证. 目前，非线性颤振系统的数值模拟方法多以Runge-Kutta方法为主[9]. 具体地，对于极限环振动，若采用数值模拟方法，则需要在较长的积分时间范围对系统求解，当系统响应呈现明显的周期性后再截取周期响应，从而获得极限环的数值解. 目前，对于一般的系统以及不同的初始条件，系统何时出现周期响应并没有得到有效的判断依据[15]. 因此，如何判断系统响应的周期性，具有较大的主观性.

本文依据Lagrange动力学原理，建立了二元机翼的非线性颤振模型. 基于Matlab计算平台，调用自带程序ode45计算了该颤振模型.

1　非线性动力系统

1.1二元机翼模型的建立

以非线性气动弹性力学方程为求解对象. 所谓二元机翼是一种假想的机翼，它的每个剖面都是相同的，各剖面之间没有相对的位移和转动. 机翼的弯曲和扭转变形可以分别用机翼刚轴(或称为弹性轴)的上下平移和对刚轴的转动来表示.

如图1所示，在二元机翼的扭心E点处固定1个刚度为Kh的抗弯弹簧和1个抗扭刚度为Kα的盘旋弹簧，此模型具有2个自由度，即上下平移h(向下为正)及俯仰角α(抬头为正). 气流的速度为v，空气动力中心F也称焦点，在亚音速不可压缩情况下，它在距离机翼剖面前缘的1/4弦长处. 机翼的宽度为1个单位，弦长扭心E在半弦点后的ab处，a是一无量纲系数，其值以在扭心E点之后为正，于是焦点F到扭心E的距离为D=0.5b+ab=(0.5+a)b. 机翼重心(c.g.)到扭心的距离为xαb，xα为重心在扭心之后的距离的无量纲量.

图1　二元机翼简图

1.2系统方程

在非定常亚音速气动力作用下，含立方非线性俯仰刚度的机翼的气动弹性力学方程[10]32

(1)

(2)

1.3方程的求解

为了消除方程(2)的积分部分，LEE等[9] 225引入4个变量

那么，方程(1)可改为无量纲的微分方程：

(3)

其中,系数c0,c1,…,c10以及d0,d1,…,d10如下[9] 225

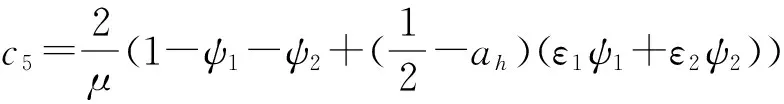
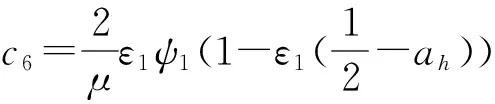
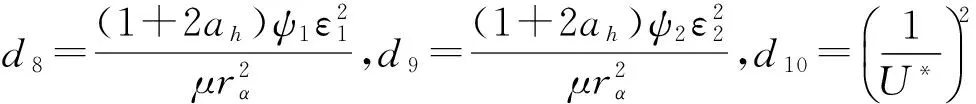
另外，f(t)和g(t)为初始状态，Wagner函数和外荷载共同确定，即

(4)

j(-c0d4+c4d0), a21=j(-c0d5+c5d0),

a22=j(-c0d3+c3d0), a23=j(-c0d4+c4d0),

a24=j(-c0d2+c2d0), a25=j(-c0d6+c6d0),

a26=j(-c0d7+c7d0), a27=j(-c0d7+c7d0),

a28=j(-c0d9+c9d0), a41=j(c1d5-c5d1),

a42=j(c1d3-c3d1), a43=j(c1d4-c4d1),

a44=j(c1d2-c2d1), a45=j(c1d6-c6d1),

a46=j(c1d7-c7d1), a47=j(c1d8-c8d1),

a48=j(c1d9-c9d1), g21=jc0d10, g41=jc1d10.

方程(4)适合采用一般的微分方程数值解法求解. 例如，可以先设定初始值X(0)，并基于Matlab计算平台直接调用ode45程序，即使用Runge-Kutta方法求解.

1.4Matlab数值模拟

基于Matlab，用Runge-Kutta数值积分法模拟方程(4)的分岔行为. 默认情况下，ode45函数的相对误差是10-3，针对相对误差为10-3和10-7这2种情况下，编制程序求解方程(4)的极限环，部分主程序如下：

options=odeset(‘RelTol’,1e-7);

t=0∶0.01∶20 000;

y0=[0.1,0,1*3.14/180,0,0,0,0,0];

[t,num]=ode45(@flutter8variable_d,t,y0,options);

t0=fix(length(t)/2);

t1=length(t);

plot(x(t0∶t1,1),x(t0∶t1,2),‘k’,x(t0∶t1,3),x(t0∶t1,4),‘k’)

另外，程序表明，积分时间足够长，而且计算结果也在后半积分段内显示出来，因此，方程(4)基本上表现为长期的振动形态.

2　结果及讨论

2.1单周期极限环解

2.2三周期极限环解

2.3双周期极限环解

实际上，当相对精度调节为10-7时，计算结果(图5)显示，系统只出现单周期极限环解. 由此看来，将Runge-Kutta法的精度设置为Matlab默认精度可能出现错误的结果. 因此，用Runge-Kutta法计算非线性振动系统的周期解时，应当特别注意计算精度的影响.

图5Runge-Kutta法得到的方程(4)的限环

Figure 5Limit cycle for equation (4) obtained by Runge-Kutta method

3　结论

基于Matlab计算软件，采用Runge-Kutta四阶隐式格式积分法计算了二元机翼非线性颤振系统. 研究发现，Runge-Kutta算法相对精度对结果的定性性质影响很大，可能导致关于解周期性的错误判断，因此在应用该方法在求极限环或周期解时应当将相对误差值设定为较小的值.

[1]WANG C C, CHEN C L, YAU H T. Bifurcation and chaotic analysis of aeroelastic systems[J]. Journal of Computational and Nonlinear Dyamics, 2014, 10(9): Art 021004,13pp.[2]林洁贤. Van der Pol方程极限环的摄动-迭代解法[J]. 华南师范大学学报(自然科学版), 1997(2): 81-84.LIN J X. Pepturbation-iterative method for limit cycles of the van der Pol equations[J]. Journal of South China Normal University (Natural Science Edition), 1997(2): 81-84.

[3]梁海华. 一类三次系统的正规形和无环性[J]. 华南师范大学学报(自然科学版), 2011(2): 28-32.

LIANG H H. Nornal form and nonex iseence of limit cycle of a class of cubic system[J]. Journal of South China Normal University (Natural Science Edition), 2011(2): 28-32.

[4]CHEN Y M, LIU J K. Nonlinear aeroelastic analysis of an airfoil-store system with a freeplay by precise integration method[J]. Journal of Fluids and Structures, 2014,46(4): 149-164.

[5]DAI H H, YUE X K, LIU C S. A multiple scale time domain collocation method for solving non-linear dynamical system[J]. International Journal of Non-linear Mechanics, 2014, 67(6): 342-351.[6]LIAO S J, WANG P F. On the mathematically reliable long-term simulation of chaotic solutions of Lorenz equation in the interval[0,10 000][J]. Science China (Physics, Mechanics & Astronomy), 2014, 57(5): 330-335.[7]CHUNG K W, HE Y B, LEE B H K. Bifurcation analysis of a two-degree-of-freedom aeroelastic system with hyste-resis structural nonlinearity by a perturbation-incremental me-thod[J]. Journal of Sound and Vibration, 2009, 320(3): 163-183.

[8]MURUA J, PALACIOS R, GRAHAM J M R. Assessment of wake-tail interference effects on the dynamics of flexible aircraft[J]. AIAA Journal, 2012, 50(7): 1575-1585.

[9]LEE B H K, PRICE S J, WONG Y S. Nonlinear aeroelastic analysis of airfoils: bifurcation and chaos[J]. Progress Aerospace Science, 1999, 35(3): 205-344.

[10]LIU L P, DOWELL E H. The secondary bifurcation of an aeroelastic airfoil motion: effect of high harmonics[J]. Nonlinear Dynamics, 2004, 37(3): 31-49.

[11]LEE B H K, LIU L, CHUNG K W. Airfoil motion in subsonic flow with strong cubic nonlinear restoring forces[J]. Journal of Sound and Vibration, 2005, 281(2): 699-717.

[12]CHEN Y M, LIU J K. Homotopy analysis method for limit cycle flutter of airfoils[J]. Applied Mathematics and Computation, 2008, 203(2): 854-863.

[13]刘菲, 杨翊仁. 立方非线性机翼的二重半稳定极限环分叉[J]. 西南交通大学学报, 2004, 39(5): 638-640.

LIU F,YANG Y R. Bifurcations of 2-multiple semistable limit cycles of airfoils with cubic nonlinearity[J]. Journal of Southwest Jiaotong University, 2004, 39(5): 638-640.

[14]张琪昌, 刘海英, 任爱娣. 具有立方非线性机翼颤振的局部分叉[J]. 天津大学学报, 2004, 37(11): 970-974.

ZHANG Q C, LIU H Y, REN A D. Local bifurcation for airfoil with cubic nonlinearities[J]. Journal of Tianjin University, 2004, 37(11): 970-974.

[15]LIAO S J, WANG P F. On the mathematically reliable long-term simulation of chaotic solutions of Lorenz equation in the interval[J]. Science China (Physics, Mechanics & Astronomy), 2014, 57(2): 330-335.

【中文责编：成文英文责编：李海航】

Remarks on Application of the Runge-Kutta Method in Simulating Limit Cycle Oscillations

HUANG Wenkai, HUAN Shi*

(School of Civil Engineering, Guangzhou University, Guangzhou 510006)

Matlab software was applied to investigate a problem in implementing the Runge-Kutta method to simulate limit cycles of nonlinear dynamical systems. This problem refers to a misjudgement of the period of limit cycle oscillation, more specifically, a period-1 solution would possibly be considered to be period-2 or period-3. The relative errors of the results can be adjusted when directly calling the Matlab programs such as ode45. Taking the strongly nonlinear flutter system of an airfoil as an example, it revealed that, a period-1 limit cycle could be erroneously simulated as a period-2 or period-3 one. The correct solution can be obtained by improving the relative accuracy. This study demonstrates that it is worthy of paying more attention to the accuracy of the Runge-Kutta method, especially when used in simulating limit cycles.

Runge-Kutta method； nonlinear dynamical system； limit cycle； relative error

2015-12-31 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

广东省科技计划项目(2013B090500123)

浣石，教授，Email:huanshi@263.net.

O322

A

1000-5463(2016)04-0021-05