三区间套下不确定型初等关联函数的构造方法
陈孝国, 边晓菲, 王存权, 蔡吉花
(1.黑龙江科技大学 理学院, 哈尔滨 150022; 2.中国矿业大学(北京) 力学与建筑工程学院, 北京 100083)
三区间套下不确定型初等关联函数的构造方法
陈孝国1,边晓菲1,王存权2,蔡吉花1
(1.黑龙江科技大学 理学院, 哈尔滨 150022; 2.中国矿业大学(北京) 力学与建筑工程学院, 北京 100083)
为完善可拓集理论中初等关联函数的构造方法,借助区间距对三区间套下不确定型一维初等关联函数的构造方法进行了研究,给出三区间套下的区间位值公式,并构造了不确定型初等关联函数,得到相关定理并进行了证明。研究表明,上述方法在考虑不可接受区间、可接受区间和满意区间基础上构造的不确定型一维初等关联函数更加有效、适用,同时也将促使可拓学理论应用范围进一步扩展。
关联函数; 区间距; 区间位值; 三区间套; 不确定型
0 引 言
可拓学是由我国学者蔡文教授于1983年提出的一门原创性学科,横跨哲学、数学和工程学等众多学科,其核心理论有基元理论、可拓集理论和可拓逻辑。可拓集理论中的可拓关联函数在实际中具有广泛的应用前景及研究价值。近几年,我国学者对关联函数的构造研究做出了较多成果,杨春燕等[1]对二区间套下一维确定型初等关联函数进行了探讨,得到若干性质。随后,李桥兴[2]提出了节域为无穷区间的一般位值概念,并构造了在中点取得最大值的初等关联函数。胡宝清等[3]提出了二区间套下区间距、位值等概念,并给出一维不确定型初等关联函数。李桥兴等[4,5]指出了文献[3]存在的不足,并在此基础上对不确定型初等关联函数进行了深入探讨。李桥兴等[6]最近又构造出了三区间套下一维确定型初等关联函数,三区间套可以描述事物特征的不可接受区间、可接受区间和满意区间,更符合实际需要。目前,已有研究成果大多只针对基元取精确点值时的确定型初等关联函数进行了探讨,对于实际应用中更为广泛的基元取值为区间值的不确定型初等关联函数构造研究文献较少。基于此,笔者对三区间套下的不确定型初等关联函数构造方法进行探讨,期望通过研究进一步完善可拓集相关理论及方法,促使关联函数具有更为广泛的应用。
1 预备知识
定义1[5]设有界区间X=〈x1,x2〉和A=〈a1,a2〉,若x2-x1 定义2[5]设X=〈x1,x2〉和A=〈a1,a2〉,且X为A的小模区间,记X的中点为x12=(x1+x2)/2,则X和A之距(简称区间距)为 定义3[6]设X=〈x1,x2〉和A=〈a1,a2〉,且X为A的小模区间,记X的中点为x12=(x1+x2)/2,点x0∈(a1,a2),若x0满足 (1)x0∈(a1,(a1+a2)/2],称 为X关于点x0和区间A的左侧距,记为ρl(X,x0,A); (2)x0∈[(a1+a2)/2,a2],称 为X关于点x0和区间A的右侧距,记为ρr(X,x0,A)。 左侧距和右侧距统称为区间侧距,记为ρ(X,x0,A)。 设A、B、C是三个有限区间,且A⊂B⊂C,称C-B、B-A和A分别表示人们对事物特征的不可接受区间、可接受区间和满意区间。也称A、B和C分别为标准正域、正域和节域。符合上述条件的3个区间称为三区间套。 定义4[6]设标准正域A=〈a1,a2〉,正域B=〈b1,b2〉和节域C=〈c1,c2〉均为有限区间,且A⊂B⊂C,则对于任意x(x∈R)称 为点x关于三区间套A、B和C的一般位置值,简称位值。 若x=xu(xu存在),则当xu∉X0时,令k(xu)=1;当xu∈X0时,令k(xu)=0⊗1,表示k(xu)既等于0又等于1;若x=xv(xv存在),则当xv∉X时,令k(xv)=-1;当xv∈X时,令k(xv)=-1⊗0,表示k(xv)既等于-1又等于0,称k(x)为点x关于三区间套X0、X和X且在X的非中点x0取最大值的一般关联函数。 定义6设A〈a1,a2〉,B〈b1,b2〉和C〈c1,c2〉是三个有限区间,且A⊂B⊂C,则对于A的任意小模区间X=〈x1,x2〉称 为区间X关于三区间套A、B、C的一般位置值,简称位值。 定理1设A=〈a1,a2〉,B=〈b1,b2〉,C=〈c1,c2〉为三个有限区间,且A⊂B⊂C,X=〈x1,x2〉为A的一个小模区间,则X关于A,B,C的三区间套位置值D(X,A,B,C)<0。 由定义6可以看出定理1的结论是显然的。 定义7设A=〈a1,a2〉,B=〈b1,b2〉和C=〈c1,c2〉是三个有限区间,且A⊂B⊂C,则对于A的任意小模区间X=〈x1,x2〉,当X、A、B,X、B、C,X、A、B、C无公共同向端点xz时,令 称k(X)为区间X关于A,B,C在B的中点取最大值的一般关联函数。 定理2设A=〈a1,a2〉,B=〈b1,b2〉,C=〈c1,c2〉为三个有限区间且A⊂B⊂C,区间X=〈x1,x2〉为A的小模区间,则k(X)满足: (1)X⊂A且无公共同向端点⟺k(X)>1; (2)X,A有公共同向端点⟺k(X)=1; (3)∃x∈X-A、X⊂B且X,A,B无公共同向端点⟺0 (4)X,B有公共同向端点⟺k(X)=0; (5)∃x∈X-B、X⊂C且X,B,C无公共同向端点⟺-1 (6)X,C有公共同向端点⟺k(X)=-1; (7)∃x∈X-C且X,C无公共同向端点⟺k(X)<-1。 证明仅证(1)、(3)、(5)、(7)。 必要性 (1)若X⊂A且无公共同向端点,有ρ(X,A)<0,ρ(X,B)<0。 分以下两种情况讨论: 若ρ(X,B)=ρ(X,A),则有k(X)=ρ(X,B)/D(X,A,B,C)+1>1; 若ρ(X,B)≠ρ(X,A),则有 k(X)=ρ(X,B)/D(X,A,B,C), D(X,A,B,C)=ρ(X,B)-ρ(X,A)<0, 即k(X)=ρ(X,B)/[ρ(X,B)-ρ(X,A)]=1+ρ(X,A)/[ρ(X,B)-ρ(X,A)]>1。 (3)当x∈X-A、X⊂B且X,A,B无公共同向端点时,有ρ(X,B)≠ρ(X,A)和ρ(X,B)<0。因此k(X)=ρ(X,B)/D(X,A,B,C)>0成立。 下面证k(X)<1。采用反证法。 假设存在x∈X-A,使k(X)≥1,则有ρ(X,B)≤ρ(X,B)-ρ(X,A),即ρ(X,A)≤0,就是说X⊂A,这与已知条件存在x∈X-A矛盾。所以有k(X)<1。 (5) 若∃x∈X-B、X⊂C且X,B,C无公共同向端点时,有ρ(X,C)<0<ρ(X,B),则k(X)=ρ(X,B)/D(X,A,B,C)<0,又由于 k(X)=ρ(X,B)/[ρ(X,C)-ρ(X,B)]=-1+ ρ(X,C)/[ρ(X,C)-ρ(X,B)]>-1, 所以-1 (7)若∃x∈X-C且X,C无公共同向端点,ρ(X,C)>0,ρ(X,B)>0,分两种情况讨论。 当ρ(X,C)=ρ(X,B)时,k(X)=ρ(X,B)/D(X,A,B,C)-1<-1; 当ρ(X,C)≠ρ(X,B)时,k(X)=ρ(X,B)/D(X,A,B,C),其中 D(X,A,B,C)=ρ(X,C)-ρ(X,B)。 要证k(X)<-1,采用反证法。 假设∃x∈X-C使k(X)≥-1,则有ρ(X,B)≤ρ(X,B)-ρ(X,C),即ρ(X,C)≤0,就是说X⊂C,这与已知条件存在x∈X-C矛盾,所以有k(X)<-1。 充分性(1)当k(X)>1时,必有ρ(X,B)<0,即X⊂B,分两种情况讨论。 若ρ(X,B)=ρ(X,A),则由X⊂B⟹ρ(X,A)=ρ(X,B)<0⟹X⊂A,有k(X)=ρ(X,B)/D(X,A,B,C)+1。 若ρ(X,B)≠ρ(X,A),则k(X)=ρ(X,B)/D(X,A,B,C)=ρ(X,B)/[ρ(X,B)-ρ(X,A)]。由k(X)>1知ρ(X,A)<0,即X⊂A。 (3) 当0 若k(X)=ρ(X,B)/D(X,A,B,C)-1,则ρ(X,B)<0⟹X⊂B,与已知∃x∈X-B矛盾。因此必有k(X)=ρ(X,B)/D(X,A,B,C)。 由k(X)>0⟹X⊂B,又由k(X)<1⟹ρ(X,B)>ρ(X,B)-ρ(X,A)⟹ρ(X,A)>0,即∃x∈X-A。 因此当0 (5)当-1 因此当-1 (7)当k(X)<-1时,要证∃x∈X-C。采用反证法,假设X⊂C,∃x∈X-B,则k(X)=ρ(X,B)/[ρ(X,C)-ρ(X,B)]<-1,有ρ(X,B)>ρ(X,B)-ρ(X,C),即ρ(X,C)>0,也就是说∃x∈X-C,这与假设X⊂C矛盾。 所以有k(X)<-1⟹∃x∈X-C。 首先证单调递增。当x12 (1)当∃x∈X-B时,k(X)=ρ(X,B)/[ρ(X,C)-ρ(X,B)])=(x1-b1)/(b1-c1)结果表明随着x1逐渐接近b1时,k(X)单调递增。 (2)当X⊂B且x12 下面证单调递减。当x12>b12时,分两种情形讨论。 (1)当x12>b12时且X⊂B时,再细化为x12 k(X)=ρ(X,B)/[ρ(X,B)-ρ(X,A)]= (x2-b2)/(x1+x2-b2-a1), 由于X=〈x1,x2〉是一个定长区间,即x2-x1=m(常数),所以 ,k(X)=(x1+m-b1)/(2x1+m-b2-a1),k(X)关于x1求导可知k'(X)<0,所以k(X)关于x1是单调递减的;若x12>a12,则 k(X)=ρ(X,B)/[ρ(X,B)-ρ(X,A)]= (x2-b2)/(a2-b2), 结果表明k(X)随着x2增加而单调递减。 (2)当x12>b12且∃x∈X-B时,再细化为x12>c12或x12 k(X)=ρ(X,B)/[ρ(X,C)-ρ(X,B)]= (x2-b2)/(b2-c2), 结果表明k(X)随着x2的增加而单调递减。 若x12 (1)x0∈(a1,(a1+a2)/2],称 (2)x0∈[(a1+a2)/2,a2],称 为X关于x0和A的右侧距,记为ρr(X,x0,A)。 定义9 (最大值在x0处取得的关联函数)设A=〈a1,a2〉,B=〈b1,b2〉和C=〈c1,c2〉是三个有限区间,且A⊂B⊂C,则对于A的任意小模区间X=〈x1,x2〉,当X、A、B,X、B、C,X、A、B、C无公共同向端点时,令 称k(X)为区间X关于A,B,C在B中x0处取最大值的一般关联函数。 在已有二区间套下的区间距及位值公式基础上,构造了三区间套下的不确定型初等关联函数,得到相关性质,并给出了证明。由于复杂事物的信息往往具有不确定性,人们很难获取事物特征的精确值,因此基元的取值从精确的点值拓展到区间值,将使不确定型初等关联函数在实际应用中更加广泛。同时,三区间套使得关联函数能够更加细致的描述事物的变化过程,提高可拓学相关理论在解决社会经济、工程技术、人工智能等领域矛盾问题的实用性及有效性。 [1]杨春燕, 蔡文. 可拓集中关联函数的研究进展[J].广东工业大学学报, 2012, 29(2): 7-14. [2]李桥兴. 节域为负无穷区间和全体实数域的初等关联函数构造[J].系统工程理论与实践, 2012, 32(12): 2740-2744. [3]胡宝清, 王孝礼, 何娟娟. 区间上的可拓集及其关联函数[J].广东工业大学学报, 2000, 17(2): 101-104. [4]李桥兴, 刘思峰. 一般位值公式及一般初等关联函数构造方法[J].系统工程, 2006, 24(6): 116-118. [5]李桥兴, 刘思峰. 基于区间距和区间侧距的初等关联函数构造[J].哈尔滨工业大学学报, 2006, 38(7): 1097-1100. [6]李桥兴, 杨春燕. 正域为有限区间的三区间套一维关联函数[J]. 科技导报, 2014, 32(36): 48-51. (编辑徐岩) Construction method of uncertain type elementary dependent function in three nested intervals CHENXiaoguo1,BIANXiaofei1,WANGCunquan2,CAIJihua1 (1. College of Science, Heilongjiang University of Science & Technology, Harbin 150022, China;2. School of Mechanics & Civil Engineering, China University of Mining & Technology, Beijing 100083, China) This paper is an attempt to improve the construction method of elementary dependent function in extension set theory. The improvement is achieved by investigating the construction method of uncertain type one-dimensional elementary dependent function in three nested intervals by the interval distance; producing the interval position value formula in three nested intervals; developing the uncertain type elementary dependent function; and ultimately verifying the related theorem obtained. This research suggests that the above method could work more effectively for the uncertain type one-dimensional elementary dependent function developed out of the consideration of unacceptable interval, acceptable interval and satisfied interval and promises a wider application of extenics theory. dependent function; interval distance; interval position value; three nested intervals; uncertain type 2015-12-07 黑龙江省自然科学基金项目(QC2015055);黑龙江省教育厅科学技术研究项目(12531577);中国矿业大学(北京)博士研究生拔尖创新人才培育基金项目(20150606) 陈孝国(1978-),男,黑龙江省克东人,副教授,博士,研究方向:复杂决策理论,E-mail:kjdxcxg@sohu.com。 10.3969/j.issn.2095-7262.2016.01.023 N945.16 2095-7262(2016)01-0106-04 A
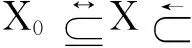
2 三区间套下不确定型初等关联函数



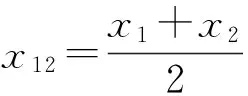

3 结束语

