σ-弱本质有界函数和σ-弱可表示算子❋

魏常果， 王苍园

(中国海洋大学数学科学学院，山东 青岛 266100)



σ-弱本质有界函数和σ-弱可表示算子❋

魏常果， 王苍园

(中国海洋大学数学科学学院，山东 青岛 266100)

本文引入了σ-弱本质有界算子函数及σ-弱可表示; 证明了L(Ω,M)中的元素都能表示成Ω上的σ-弱可列可加算子测度, 即存在等距映射将L(Ω,M)等距嵌入Ba(R)中。 还刻画了L(Ω,M)上线性算子和线性泛函的性质; 最后证明了L(Ω,μ)上算子T为σ-弱可表示算子的充要条件。

von Neumann代数；σ-弱本质有界； σ-弱可表示

引用格式：魏常果，王苍园.σ-弱本质有界函数和σ-弱可表示算子 [J].中国海洋大学学报(自然科学版), 2016, 46(10):135-138.

WEI Chang-Guo， WANG Cang-Yuan. σ-Weakly essentially bounded functions and σ-weakly representable operators [J].Periodical of Ocean University of China, 2016, 46(10):135-138.

1　引言

算子代数在某种意义上被认为是研究非交换拓扑, 传统分析和拓扑的许多理论在算子代数上都有对应, 如K-理论来自拓扑K-理论, KK-理论来自伪微分算子理论。 这极大地丰富了算子代数理论, 并加强了算子代数与其它数学分支的联系。 经典调和分析被认为是交换的分析学, 到如今它已是十分完备,与此对应, 考虑算子代数意义下的调和分析是自然的, 这种非交换调和分析自上世纪九十年代初兴起以来正日益受到重视, 这无疑会促进算子代数的发展和它在其它数学分支中的应用。 K.Matsumoto在文献[1-2]中将Schwartz的分布理论推广到算子代数, 并利用它求解C*代数上的微分方程。 Wu在文献[3]中研究了取值于算子代数的广义函数, 得到了算子值的Bochner-Schwartz定理。文献[4]还研究了半群上的非交换分析。 测度与积分是调和分析研究的主要对象。 文献[5]中引进了取值于von Neumann代数的测度, 证明了σ-弱拓扑下的Kluvanek延拓定理;文献[6]中引入了算子测度和算子函数的σ-弱积分,证明了Ba(R)等距同构于L(B(X,R);M); 给出了σ-弱算子拓扑下的Riesz表示定理; 文献[7-9]中研究了Banach*代数中的半序及环面代数扩张的分类等问题。

在本文中, 引入σ-弱本质有界算子值函数及σ-弱可表示; 刻画了L(Ω,M)上线性算子和线性泛函的性质, 最后给出了L(Ω,μ)上算子T为σ-弱可表示算子的充要条件。

设M为一von Neumann代数, X为任一集合,R为X的子集构成的σ-域。 从R到M的有限可加集映射μ被称作上R的算子测度。

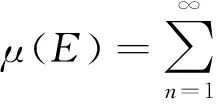
2　主要结果

设M为作用在Hilbert空间H上的von Neumann代数, M*为M的准共轭空间, 即M上的正规线性泛函全体(在σ-拓扑下连续的正线性泛函)。设(Ω,R,μ)为完备的全σ-有限测度空间, L(Ω,μ)为Ω上的可积复值函数全体, L∞(Ω,μ)为Ω上的本质有界的复值函数全体。

定义2.1[6]称算子值函数f:Ω→M在(Ω,R,μ)上是σ-弱可测的, 若∀ρ∈M*, 数值函数ρ。f是(Ω,R,μ)上的可测函数。

定义2.2[6]称算子值函数f:Ω→M是 σ-弱可积的, 若对于E∈R, 存在TE∈M, 使得

∀ρ∈M*, 积分∫Eρ(f(t))dμ存在, 且

ρ(TE)=∫Eρ(f(t))dμ。

此时称TE为f在E上的σ-弱积分, 记作

TE=∫Ef(t)dμ。

Ω上σ-弱可积的算子值函数全体记作L(Ω,M)。

定义2.3[6]设μ:R→M为算子测度。 μ的σ-弱半变差‖μ‖定义为:

‖μ‖(E)=sup{|ρμ|(E):ρ∈(M*)1}。

若‖μ‖(X)<∞, 则称μ为σ-弱有界半变差测度,或简称为σ-弱有界测度。 R上有限可加的σ-弱有界测度全体构成的线性空间记作Ba(R)。 易证Ba(R)在范数 ‖μ‖1=‖μ‖(X) 下构成赋范空间。

在L(Ω,M)内引入等价关系: f,g∈L(Ω,M), 若∀ρ∈M*, 有ρ。f=ρ。ga.e., 则称f与g等价。 将等价的函数视为相等, 则可在L(Ω,M)中引入范数:

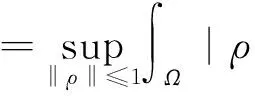
由[6]定理3.1的证明可知L(Ω,M)该范数下构成赋范空间。

定义2.4设f:Ω→M为σ-弱可测函数。 若∀ρ∈M*, 且‖ρ‖≤1, 使得ρ。f本质有界, 且

sup{‖ρ。f‖∞:‖ρ‖≤1}<∞,

则称f为σ-弱本质有界的算子值函数, 这样的函数全体记作L∞(Ω,M)。

设f∈L∞(Ω,M), 令

‖f‖∞=sup{‖ρ。f‖∞:‖ρ‖≤1},

可验证‖·‖∞为L∞(Ω,M)上的范数。

设L(Ω,M)*为L(Ω,M)在前述范数下的对偶空间。 B(L(Ω,M);M)为L(Ω,M)到M的有界线性算子全体。

下面的定理说明L(Ω,M)与Ba(R)、M*与L(Ω,M)*、L∞(Ω,μ)与B(L(Ω,M);M)在等距的意义下, 具有包含关系。

定理2.1 L(Ω,M)中的元素都能表示成Ω上的σ-弱可列可加算子测度, 即存在等距映射将L(Ω,M)等距嵌入Ba(R)中。

证明设f∈L(Ω,M), 令

F(E)=∫Efdμ，∀E∈R。

由[6]定理3.1的证明可知, F的定义是有意义的, 且F具有有限可加性。 任给ρ∈M*, 有

(ρF)(E)=ρ(F(E))=∫Eρ(f(t))dμ。

因为ρ。f∈L(Ω,μ), 所以ρF为可列可加数值测度, 从而F为σ-弱可列可加算子测度。

由定义2.3,

‖F‖(E)=sup{|ρF|(E):ρ∈M*,‖ρ‖≤1}。

又因为|ρF|(E)=∫E|ρ。f|dμ, 所以

‖F‖(E)=sup{∫E|ρ。f|dμ:‖ρ‖≤1},

定理2.2 M*⊂L(Ω,M)*, 即存在等距映射S将M*嵌入L(Ω,M)*中。

证明任给g∈M*, 作L(Ω,M)上的泛函Sg,

Sg(f)=∫Ωg。fdμ,

其中f∈L(Ω,M), 易知Sg是线性泛函。

当g≠0时, 令g1=g/‖g‖, 则

|Sg(f)|≤∫Ω|g。f|dμ=

‖g‖∫Ω|g1。f|dμ≤‖g‖‖f‖。

所以Sg为L(Ω,M)上的有界线性泛函, 且‖Sg‖≤‖g‖。

下证: ‖Sg‖≥‖g‖。

取E⊆Ω, 使得μ(E)>0。 设a=1/μ(E),

T∈M,‖T‖≤1, 令

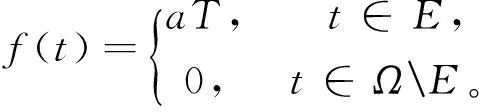
则f∈L(Ω,M)。 且

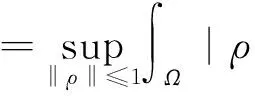
所以

‖Sg‖≥|Sg(f)|=|∫Ωg。fdμ|=|g(T)|

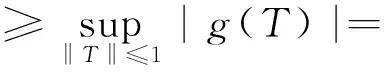
从而S为M*到L(Ω,M)*中的等距算子。

定理2.3存在等距映射将L∞(Ω,μ)嵌入B(L(Ω,M);M)中。

证明任给g∈L∞(Ω,μ), 作L(Ω,M)到M的线性算子T, 使得对任给h∈L(Ω,M)有

T(h)=∫Ωg(t)h(t)dμ。

首先易知: g∈L∞(Ω,μ),h∈L(Ω,M)时, 必有gh∈L(Ω,M)。 又

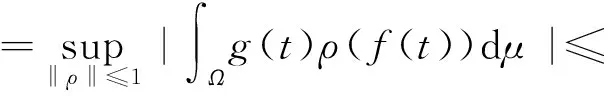
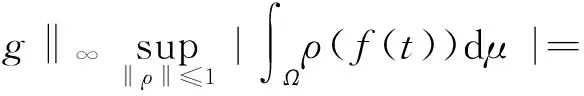
‖g‖∞‖h‖

所以‖T‖≤‖g‖∞, 即得T∈B(L(Ω,M);M)。

任给w∈L(Ω,μ), 令f(t)=w(t)p, p为M中的单位元。 则f∈L(Ω,M), 且‖f‖=‖w‖1。

即可将L(Ω,μ)视为L(Ω,M)的子空间。 又因为L(Ω,μ)*=L∞(Ω,μ), 所以

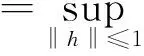
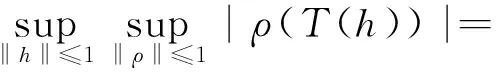
sup{|∫Ωg(t)ρ(h(t))dμ|:‖h‖≤1,‖ρ‖≤1}≥

sup{|∫Ωg(t)w(t)dμ|:w∈L(Ω,μ),‖w‖1≤1}=

‖g‖∞，

算子的可表示性是有界线性算子的重要性质, 下面定义了线性算子的σ-弱可表示, 并给出了充要条件。

定义2.5 设T:L(Ω,μ)→M为有界线性算子,若存在f∈L∞(Ω,M), 使得

Tg=∫Ωgfdμ,∀g∈L(Ω,μ),

则称T是σ-弱可表示的。

定理2.4设T:L(Ω,μ)→M为有界线性算子,令F(E)=TχE, E∈R, 这里χE为E的特征函数。 则T为σ-弱可表示的充要条件是存在f∈L(Ω,M),使得

F(E)=∫Efdμ,E∈R。

此时f∈L∞(Ω,M), 且‖T‖=‖f‖∞。

证明: 必要性。 T为σ-弱可表示的, 则存在

f∈L∞(Ω,M), 使得Tg=∫Ωgfdμ,

从而∀E∈R, 有

F(E)=TχE=∫ΩχEfdμ=∫Efdμ。

充分性。 设f∈L(Ω,M), 使得∀E∈R,

F(E)=TχE=∫Efdμ。 ∀ρ∈M*, ‖ρ‖≤1, 有

|ρ(F(E))|≤‖F(E)‖≤‖T‖‖χE‖1=

‖T‖μ(E),

所以

|ρF|(E)≤‖T‖μ(E),

‖F‖(E)=sup{|ρF|(E):‖ρ‖≤1}≤

‖T‖μ(E)。

由定理2.1, F为σ-弱可列可加测度, 且

‖F‖(E)=sup{∫E|ρ∘f|dμ:‖ρ‖≤1}。

所以

sup{∫E|ρ∘f|dμ:‖ρ‖≤1}≤‖T‖μ(E),

从而∀ρ∈M*, ‖ρ‖≤1有

∫E|ρ。f|dμ≤‖T‖μ(E),

所以‖ρ。f‖∞≤‖T‖。 因此

‖f‖∞=sup{‖ρ。f‖∞:‖ρ‖≤1}≤‖T‖,

即得f∈L∞(Ω,M)。

由于简单可积函数在L(Ω,μ)中稠密, 所以对∀g∈L(Ω,μ)存在简单可积函数列{φn}, 使得‖φn-g‖1→0。 T有界, 所以‖Tφn-Tg‖→0。

由于Tφn=∫Ωφnfdμ, 及f∈L∞(Ω,M), 对于

ρ∈M*, 有

ρ(Tφn)=∫Ωρ(φnf)dμ=∫Ωφn(t)ρ(f(t))dμ。

ρ∘f∈L∞(Ω,μ), 由Lebesgue控制收敛定理得:

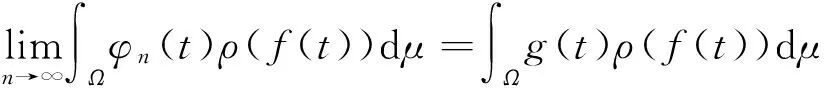
所以

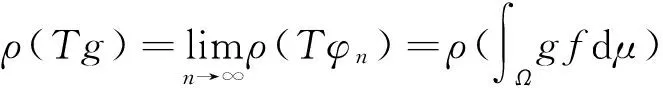
从而Tg=∫Ωgfdμ, T是σ-弱可表示的。

最后,

‖Tg‖=‖∫Ωgfdμ‖=

sup{|ρ(∫Ωgfdμ)|:ρ∈M*,‖ρ‖≤1}=

sup{|∫Ωg∘(ρ。f)dμ|:ρ∈M*,‖ρ‖≤1}≤

sup{‖g‖1‖ρ。f‖∞:ρ∈M*,‖ρ‖≤1}=

‖f‖∞‖g‖1,

所以‖T‖≤‖f‖∞。 因此‖T‖=‖f‖∞。

[1]Matsumoto K. Periodic distributions on C*-algsbras [J]. J Math Soc Japan, 1995, 47 (4): 687-718.

[2]Matsumoto K. Distributions on C*-algebra associated whih Rn-actions [J]. Proc London Math, 1997, 74 (3): 444-480.

[3]Wu L S. Positive-definite generalized functions on operator algebras [J]. Chinese J Contemp Math, 1997, 18 (1): 127-136.

[4]Wu L S. Non-commutative harmonic analysis on semgroups [J]. Chin Ann of Math, 1998, 19A (5): 583-588.

[5]Wei C G. On measures with values in von Neumann algebras [J]. Journal of Xi’an United University (Natural Sciences Edition), 2000, 3(4): 18-23.

[6]Wei C G. Measures and integrations on σ-weak operator topology [J]. Journal of Mathematical Study, 2001, 34(3): 96-101.

[7]Wei C G. Some properties of partial order in Banach* algebras [J]. Journal of East China Normal University (Natural Science), 2005, 2005(1): 23-27.

[8]Wei C G. Homomorphisms from extensions of torus algebra [J]. Acta Mathematica Sinica, Chinese Series, 2006, 49(4): 791-796.

[9]Wei C G. Classification of extensions of C(T2) II [J]. Science China Mathematics, 2012, 55(1): 179-186.

AMS Subject Classification：46L50

责任编辑陈呈超

σ-Weakly Essentially Bounded Functions andσ-Weakly Representable Operators

WEI Chang-Guo， WANG Cang-Yuan

(School of Mathematical Sciences, Ocean University of China, Qingdao 266100， China)

This paper introduces the σ-weakly essentially bounded functions and σ-weakly representable operators. Let M be a von Neumann algebra, X be any set and R be a σ-field of subsets of X.An operator valued measure μ on R is a map from R into the finitely additive subsets of M. Let {En} be a family of any mutually disjoint subsets of R, E be the union. If μ is countably additive on {En}, with respect to the σ-weakly operator topology, then μ is called σ-weakly countably additive measure. Every σ-weakly integrable operator valued function in L(Ω,M) can be represented to be a σ-weakly countably additive measure on Ω, i.e. there exists an isometric embedding from L(Ω,M) into Ba(R). The space of normal linear functionals on Mcan be isometrically embedded into L(Ω,M)*. And there is also an isometry from L∞(Ω,μ) into B(L(Ω,M);M). The equivalent characterization of a σ-weakly representable operator is given at the end of this paper.

von Neumann algebra; σ-weakly essentially bounded; σ-weakly representable

山东省自然科学基金项目(ZR2011AM003)；国家自然科学基金项目(11171315)资助

2014-06-20；

2015-10-11

魏常果(1971-)，男，教授。E-mail:weicgqd@163.com

O177.1

A

1672-5174(2016)10-135-04

10.16441/j.cnki.hdxb.20140333

Supported by Shandong Provincial Natural Science Foundations (ZR2011AM003); National Natural Science Foundations of China (11171315)