可对角化矩阵的特征值与特征空间的扰动
黎 稳, 陈艳美, 莫荣华
(1. 华南师范大学数学科学学院, 广州 510631; 2. 广东技术师范学院计算机科学学院, 广州 510665;3. 广东工业大学应用数学学院, 广州 510006)
可对角化矩阵的特征值与特征空间的扰动
黎 稳1*, 陈艳美1,2*, 莫荣华3
(1. 华南师范大学数学科学学院, 广州 510631; 2. 广东技术师范学院计算机科学学院, 广州 510665;3. 广东工业大学应用数学学院, 广州 510006)
矩阵特征值和特征空间的计算是数值代数的重要课题之一,在科学工程计算等领域有重要的作用. 而特征值与特征空间的扰动分析是有关特征值数值分析的一个重要研究方向,它的经典结果分别是特征值扰动的Hoffman-Wielandt定理和特征空间的sinθ定理. 文中所考虑的是可对角化矩阵的乘法与加法扰动下的特征值与特征空间的组合扰动分析,给出了组合扰动界,所得到的结果推广了Hermite矩阵的组合扰动的相关结果. 另一方面,从新得到的结果可以分别导出有关特征值和特征空间的扰动界.
可对角化矩阵; 加法扰动界; 乘法扰动界
许多科学与工程计算都涉及矩阵特征值计算问题,而特征值的敏感性分析是特征值的数值分析中的重要方向. 不少学者研究了特征系统的扰动界[1-8],提出了矩阵分解的一些组合扰动界[6-7,9-10].特别地,给出了Hermitian矩阵的特征系统的一些组合扰动界[6-7]. 为了对矩阵的特征系统给出组合扰动界,首先介绍一些符号.

AX=X,

(1)
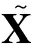
(2)

(3)


(4)
众所周知,矩阵的扰动有2种不同的方式:
定义
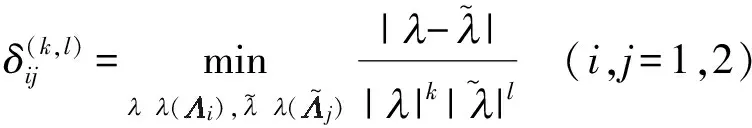
(5)


(6)






(7)

界(7)的1个渐近形式是




(8)
本文首先给出了加法扰动的组合扰动界,改进了界(7)的结果;然后得到了乘法扰动的组合扰动界,推广了式(8)的结果.
1 加法扰动界
本节主要得到特征值与特征空间在加法扰动下的组合扰动界. 首先给出一些引理.
引理1[12]52假定X=(X1,X2)n×n是一个非奇异矩阵,其中X1n×m,那么对于2-或者F-范数‖·‖和任意的列满秩矩阵n×m,有 ‖‖≤‖‖2‖‖2‖‖,
(9)
其中用M†表示矩阵M的Moore-Penrose逆.
引理2[13]167设TCn×n和i=diag(n×n(i=1,2,3,4),则一定存在集合〈n〉的一个置换,使得‖1T2-3T4‖,
(10)
其中σmin(T)是矩阵T的最小奇异值.
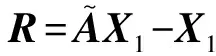


(11)
证明 由式(1)可得

再由式(4)可得


(12)
显然有
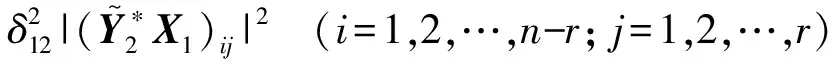

(13)
综合式(4)和式(5)可得

(14)
再由引理1 和引理2,存在集合〈r〉的转置,使得


从而证明了式(11).


(15)
其中κ(X)=‖X‖2‖X-1‖2是矩阵X的谱条件数. 不等式(15)可见文献[14]335和文献[15]107.
由式(11)可得sinθ型定理[16]. 事实上,有
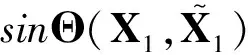
(16)

2 乘法扰动的情形
引理3[5]475-476已知Ωs×s和Γt×t是2个Hermite矩阵,而且E,Fs×t. 如果(Ω)(Γ)=∅,那么ΩX-XΓ=ΩE+FΓ有唯一解Xs×t,而且
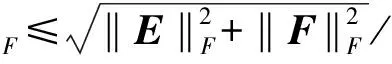
引理4[6]245已知=diag(1,…,r)和(1,…,r)满足,则一定存在集合〈r〉的一个置换,使得

下面给出可对角化矩阵的特征值和特征空间的组合扰动界.
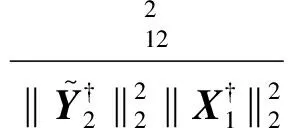
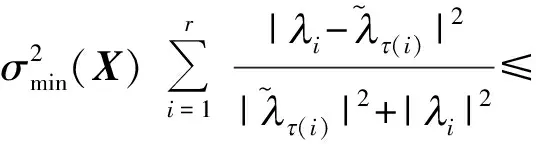

(17)


(18)


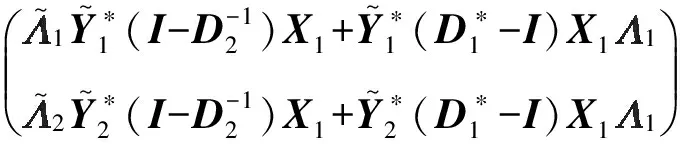
从而得到


(19)
和

(20)
把引理3用到式(19)可得

(21)
又由引理1可得

(22)
由式(21)和式(22)可得


(23)
由引理4 和式(20)可得存在〈r〉上的置换,使得


再结合式(23)可以得到




由此证明了定理2.



[1] CHEN X X,LI W. A note on the perturbation bounds of eigenspaces for Hermitian matrices[J]. Journal of Computational and Applied Mathematics,2006,196(1):338-346.
[2] IPSEN I C F. Relative perturbation results for the matrix eigenvalues and singular values[J]. Acta Numerica,1998,7(1):151-201.
[3] IPSEN I C F. A note on unifying absolute and relative perturbation bounds[J]. Linear Algebra and Its Applications,2003,358(2):239-253.
[4] LI R C. Relative perturbation theory:(I) Eigenvalue and singular value variations[J]. SIAM Journal on Matrix Analysis and Applications,1998,19(4):956-982.
[5] LI R C. Relative perturbation theory:(II) Eigenspace and singular subspace variations[J]. SIAM Journal on Matrix Analysis and Applications,1998,20(2):471-492.
[6] LI W. Multiplicative perturbation bounds for spectral and singular value decompositions[J]. Journal of Computational and Applied Mathematics,2008,217(1):243-251.
[7] LI W,SUN W W. Combined perturbation bounds I:Eigensystems and singular value decomposition[J]. SIAM Journal on Matrix Analysis and Applications,2007,29(2):643-655.
[8] DOPICO F M,MORO J,MOLERA J M. Weyl-type relative perturbation bounds for eigensystems of Hermitian matrices[J]. Linear Algebra and Its Applications,2000,309(1):3-18.
[9] CHEN Y M,CHEN X S,LI W. On perturbation bounds for orthogonal projections[J]. Numerical Algorithms,2016,doi:10. 1007/s11075-016-0102-2.
[10]LI W,SUN W W. Combined perturbation bounds:II. Polar decompositions[J]. Science in China:Series A,2007,50(9):1339-1346.
[11]STEWART G,SUN J G. Matrix perturbation theory[M]. Boston:Academic Press,1990.
[12]LI W,CHEN X X. Some residual bounds for approximate eigenvalues and approximate eigenspaces[J]. Journal of Computational Mathematics,2012,30(1):47-58.
[13]ElSNER L,FRIEDLAND S. Singular values,doubly stochastic matrices and applications[J]. Linear Algebra and Its Applications,1995,220(1):161-169.
[14] 孙继广. 关于正规矩阵特征值的扰动[J]. 计算数学,1984(3):334-336.
SUN J G. On the perturbation of the eigenvalues of a normal matrix[J]. Mathematica Numerica Sinica,1984(3):334-336.
[15] 张振跃. 关于非亏损矩阵特征值的扰动[J]. 计算数学,1986(1):106-108.
ZHANG Z Y. On the perturbation of the eigenvalues of a non-defective matrix[J]. Mathematica Numerica Sinica,1986(1):106-108.
[16] DAVIS C,KAHAN W. The rotation of eigenvectors by a perturbation:III[J]. SIAM Journal on Numerical Analysis,1970,7(1):1-46.
【中文责编:庄晓琼 英文责编:肖菁】
Perturbation Bounds of Eigenvalues and Eigenspaces for Diagonalizable Matrices
LI Wen1*, CHEN Yanmei1,2*, MO Ronghua3
(1. School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China; 2. School of Computer Science, Guangdong Polytechnic Normal University, Guangzhou 510665, China; 3. School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510006, China)
The computation for eigenvalues and eigenspaces is one of the important research fields in numerical algebra, and it plays an important role in scientific Engineering computations. The perturbation analysis for eigenvalues and eigenspaces is one of the significant topics in the numerical analysis in eigenvalue computing. The classical perturbation results are the Hoffman-Wielandt theorem for eigenvalue perturbation and the sinθfor the eigenspace. In this paper, the combined perturbation analysis for the matrix and it’s perturbed matrix being diagonalizable matrices under the additive and the multiplicative perturbation are considered, and their combined perturbation bounds are given, respectively, which extend the corresponding combined perturbation result for the Hermitian matrix case. On the other hand, the eigenvalue perturbation bound and the eigenspace perturbation bound can be derived from the new bounds, respectively.
diagonalizable matrix; additive perturbation bound; multiplicative perturbation bound
2016-05-12 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n
国家自然科学基金项目(11271144,11571124,11671158,11601340); 中山大学广东省计算科学重点实验室开放基金项目(2016016); 广东技术师范学院青年科研项目
O241.6
A
1000-5463(2016)05-0082-04
*通讯作者:黎稳,教授,Email:liwen@scnu.edu.cn;陈艳美,讲师,Email:chch1980@163.com.

