欧氏空间凸多面体极点凸组合表示定理的推广
姚志敏
(广东培正学院计算机科学与工程系,广东 广州 510830)
欧氏空间凸多面体极点凸组合表示定理的推广
姚志敏
(广东培正学院计算机科学与工程系,广东 广州 510830)
使用切面技术、归纳法等证明了欧氏空间中凸集极点的存在性,进一步证明了空间中一般有界闭凸集(不只局限于凸多面体)中任意一点同样可表示为极点的凸组合.方法独到.
凸集;凸组合;极点;切平面;仿射集
1 引言
线性规划领域[1-2]常有提出n维欧氏空间(后续简记为Rn)中有界凸集中任意一点可由此集合极点的凸组合表示,但其所涉及的凸集只局限于凸多面体[1,3],且一般著述中鲜有进行证明.事实上,进一步推广,对于n维欧氏空间中一般有界闭凸集S,任意一点x∈S同样可表示为S的极点的凸组合.
2 预备知识
定义 2.1[1]若集合M ⊂Rn包含所有通过其内任意两点的直线,即∀x1,x2∈M,λ∈R有

则称M 为一个仿射集(仿射流形).
命题 2.1[4]一个仿射集的平移也是仿射集,Rn的子空间是包含原点的仿射集.
定义 2.2[1]非空仿射集M 的维数是指平行于仿射集M 的子空间的维数,Rn中任意集合S的维数为包含S的仿射集的最小维数.
定义 2.3[5]设S⊂Rn,若对任意x1,x2∈S和任意数λ∈[0,1],有
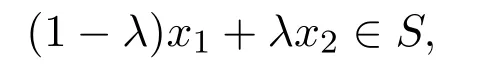
则称S为Rn中的凸集.
设
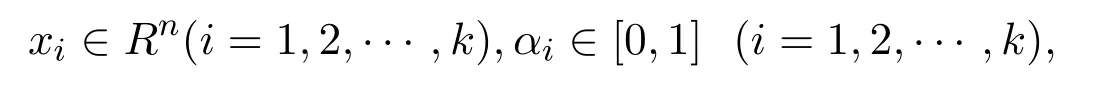
且

命题 2.2[4,6]凸集的交集还是凸集,闭凸集的交集还是闭凸集.
定义 2.4[6]设S是凸集,x0∈S,若x0不能用不同的两点x1∈S,x2∈S的线性组合表示,即

则称x0为S的一个极点(顶点).
定义 2.5[1]对于给定的非零向量PT=(p1,p2,…,pn)和实数β(这里x为列向量),集合

称为Rn中的超平面.集合
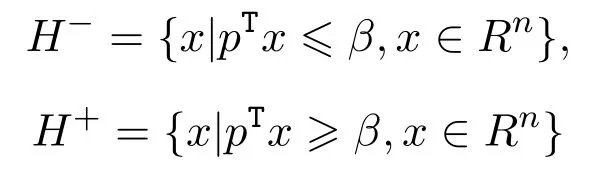
称为Rn中的闭半空间,即由超平面H所划分的两个闭半空间.
命题 2.3[1]Rn中超平面H等同n−1维仿射集,即某一n−1维子空间的平移.
3 主要结果一:n维欧氏空间中凸集极点的存在性
显然,Rn中凸集不一定存在极点.例如,给定x1,x2∈Rn,经过两点的直线
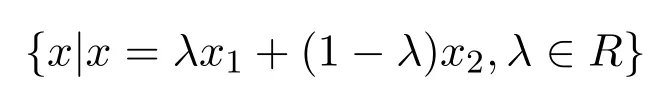
为凸集,无界且不存在极点;经过点x2的线段
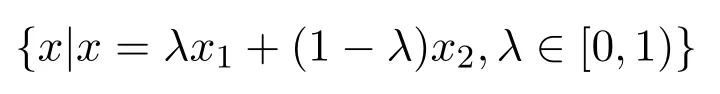
为凸集,有界且存在极点x2;单位开球{x|∥x∥<1,x∈Rn}为凸集,有界且不存在极点.
对于Rn中凸集,要研究其中任意一点可否表示为其极点的凸组合,前提是此凸集必须存在极点.
引理 3.1[7-9]设S(≠∅)为Rn中的闭凸集,y∉S,则存在非零向量p∈R及实数ε>0,使得对点x∈S,有
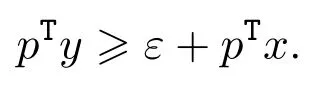

引理 3.2[5,7,10]设S(≠∅)为Rn中的闭凸集,y∈∂S(∂S为S的边界,此处∂S⊂S),则存在非零向量p∈Rn,使得对点x∈S,有pTy≥pTx,即存在经过y点的S的n−1维切平面(支撑超平面)
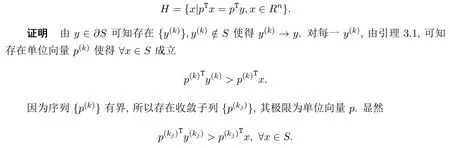


定理 3.1设S(≠∅)为Rn中有界闭凸集,则S一定存在极点.


4 主要结果二:n维欧氏空间中凸集的极点凸组合表示
Rn中凸集S即使存在极点,∀x∈S也未必能由极点的凸组合所表示.举例如下:
例 4.1∀x1,x2∈Rn,经过点x2的线段{x|x=λx1+(1−λ)x2,λ∈[0,1)}为凸集,非闭有界,(唯一)极点x2外任意一点不能由极点x2的凸组合表示;经过点x2的射线

为凸集,无界闭集,(唯一)极点x2外任意一点也不能由极点x2的凸组合表示.
例 4.2R2中,半圆{(x,y)|x2+y2≤1,x>0,x,y∈R}为凸集,非闭有界,其中任意一点能由极点的凸组合表示;集合

为凸集,无界闭集,其中任意一点也能由极点的凸组合表示;集合
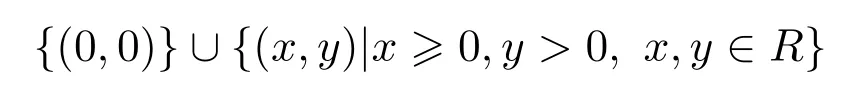
为凸集,非闭无界,极点(0,0)外任意一点却不能由极点的凸组合表示.
例 4.3R3中集合{(x,y,z)|y2+z2≤x,y>0,x,y,z∈R}为凸集,非闭无界,其中任意一点能由极点的凸组合表示.
然而,对于Rn中的有界闭凸集,情况则不一样了.
定理 4.1设S为Rn中有界闭凸集,∀x∈S总可以找到S的有限个极点x1,x2,…,xm,使得
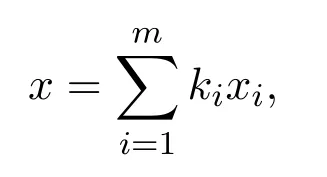
其中
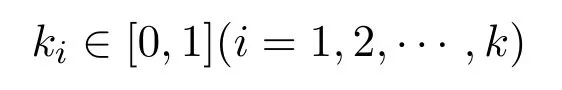
且

证明由定理3.1知Rn中有界闭凸集存在极点.数学归纳法:

注 1Rn中,由于凸多面体属于有界闭凸集中的一种特殊形式,所以线性规划领域[1,4]凸多面体中任意一点可由该多面体极点的凸组合表示,这一重要定理就成了定理4.1的一个直接推论.
5 结语
定理3.1中要直接证明S存在极点是非常困难的,所以先使用切面技术得到S的低维子集S′,再证明S′的极点同时是S的极点,最后结合归纳假设完成其证明.方法独到.
定理4.1的证明同样使用了”S′的极点同时是S的极点”这一重要结果.
定理3.1、4.1中结论有望作更进一步的推广,研究其在Banach、一般度量等空间中的成立性.
参考文献
[1]Dimitris Bertsimas,John N.Tsitsiklis.Introduction to Linear Optimization[M].Nashua:Athena Scienti fi c, 1997.
[2]谭泽光.多面体有限基定理的一个证明[J].清华大学学报:自然科学版,1988,28(3):83-90.
[3]魏权龄,汪俊,闫洪.无界凸面体由“和形式”向“交形式”的转化[J].系统工程理论与实践,2004,24(3):87-90.
[4]Leonid Nison Vaserstein,Christopher Cattelier Byrne.Introduction to Linear Programming[M].Bergen: Pearson Education,Inc.,2003.
[5]Borwein J M,Lewis A S.Convex Analysis and Nonlinear Optimization[M].2nd ed.Berlin:Springer,2006.
[6]张干宗.线性规划[M].武汉:武汉大学出版社,2004.
[7]柯尔莫戈洛夫A H,佛明C B.函数论与泛函分析初步[M].段虞荣,郑洪深,郭思旭,译.北京:高等教育出版社,2006.
[8]陈利国,罗成.关于局部凸空间的中点局部一致凸性[J].纯粹数学与应用数学,2011,27(6):749-755.
[9]Ha¨ım Brezis.Analyse Fonctionnelle-Th é orieet Applications[M].Berlin:Springer,2009.
[10]陈乔.严格r-预不变凸函数[J].纯粹数学与应用数学,2013,29(6):621-626.
[11]张恭庆,林源渠.泛函分析讲义:上册[M].北京:北京大学出版社,2008.
Generalization of the representation theorem of the convex combinations of convex polyhedron extreme points in Euclidean space
Yao Zhimin
(Department of Computer Science and Engineering,Guangdong Peizheng College, Guangzhou 510830,China)
By the techniques such as tangent plane,mathematical induction,we obtain the existence of extreme points of convex set in n-dimensional Euclidean space.We further prove,by a unique method,any point in a bounded closed convex set(not limited to convex polyhedron)can be expressed as a convex combination of the extreme points.
convex set,convex combination,extreme point,tangent plane,tangent plane
O174.13
A
1008-5513(2017)01-0019-07
10.3969/j.issn.1008-5513.2017.01.003
2016-11-06.
国家自然科学基金(11461002);广西高校科学技术研究项目基金(LX2014194).
姚志敏(1975-),硕士,讲师,研究方向:应用数学及理论.
2010 MSC:52A20

