加权Motzkin序列的Hankel行列式
李彦君,杨胜良
(兰州理工大学理学院,甘肃 兰州 730050)
加权Motzkin序列的Hankel行列式
李彦君,杨胜良
(兰州理工大学理学院,甘肃 兰州 730050)
基于经典的Motzkin路引入了一类新的加权Motzkin路的定义,用这种路给出了一类指数型Riordan矩阵的组合解释,得到了相应的Riordan矩阵第0列元素(加权Motzkin序列)的加法公式.作为应用,得到了一类加权Motzkin序列的Hankel行列式的计算方法.
指数型Riordan矩阵;加权Motzkin路;加法公式;Hankel行列式
1 引言



2 指数型Riordan矩阵的组合解释及加法公式

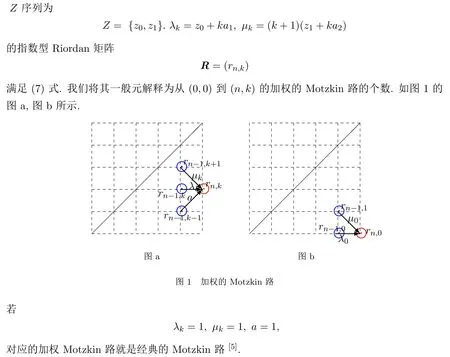
定理2.1一个Z序列为{z0,z1},A序列为{a,a1,a2}的指数型Riordan矩阵R=(rn,k)满足加法公式:

其中
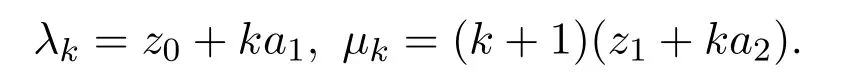

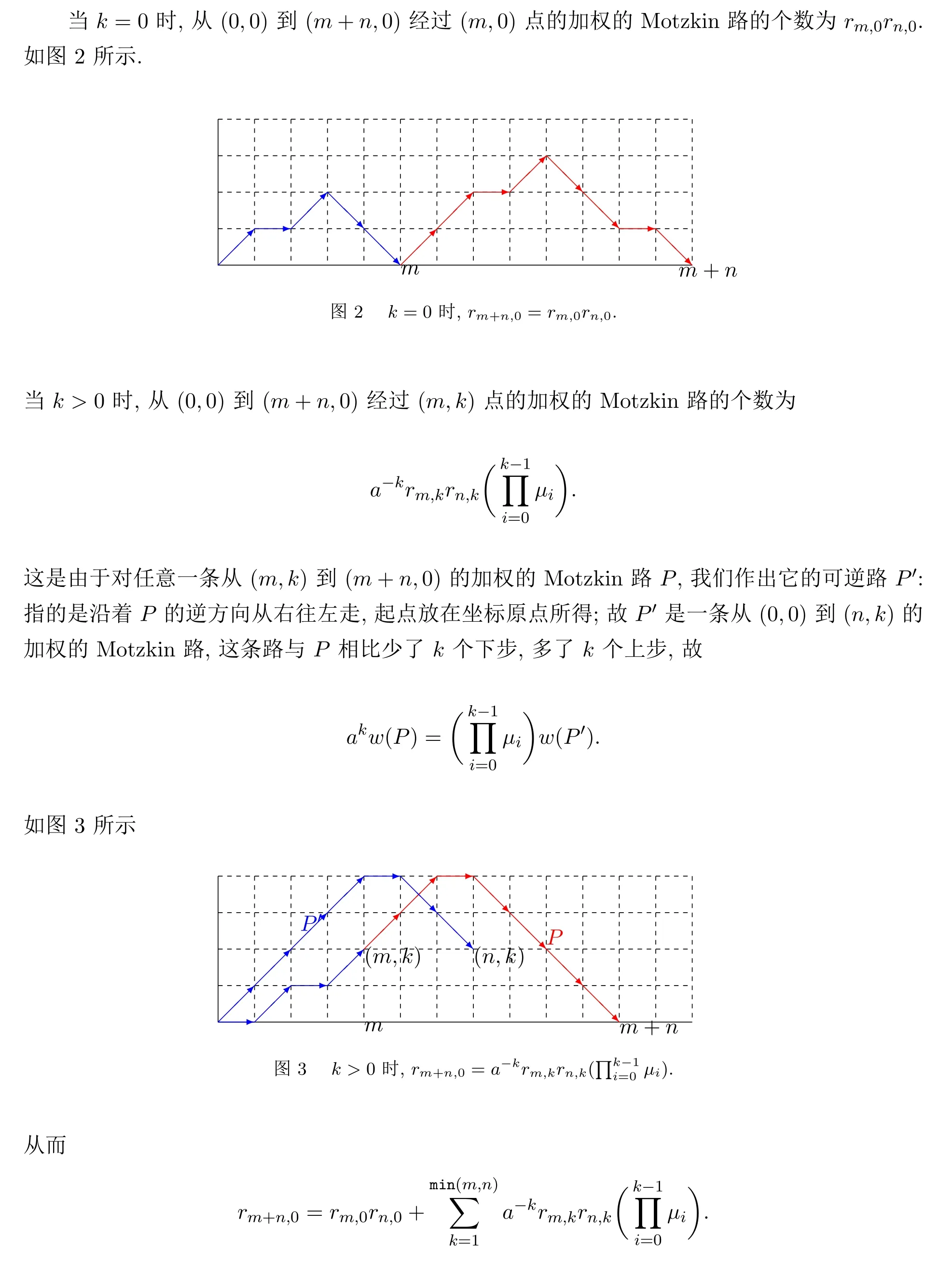
3 加权Motzkin序列的Hankel行列式及其应用
设(rn)n≥0是一个实数序列,由序列(rn)n≥0所确定的n阶Hankel矩阵[6-7]

将Z序列为{z0,z1},A序列为{a,a1,a2}的指数型Riordan矩阵[g(t),f(t)]的第0列元素(rn,0=n![tn]g(t))称为加权的Motzkin序列,记作序列(rn)n≥0.
定理 3.1加权Motzkin序列(rn)n≥0的Hankel矩阵的行列式为:

这里λk=z0+ka1,µk=(k+1)(z1+ka2).
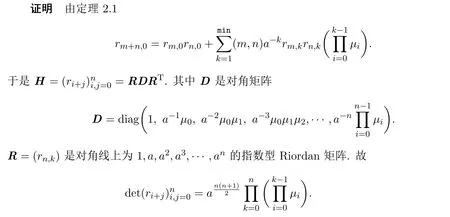
注3.1若a=1,则有
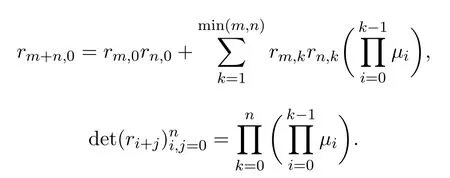
这是文献[5]的结果,在文献[5]中是用归纳法进行证明的,这里我们将其结果推广并且给出了格路证明.

注3.2当x=1时就是Bell序列A000110(文献[10])的Hankel行列式,对于x=1的情况在文献[11]中用类似的方法做的,这里我们将其做到多项式序列上去,使得应用更加广泛.



注3.3该例题的指数型Riordan矩阵对角线上的元素不全为1,是定理2.1和定理3.1的一个典型应用.在文献[5-11]中,有相似的结果.我们得到的得结果相对于文献[5-11]有以下优势:
1.本文的结论是建立在定理2.1和定理3.1基础上的,定理2.1有严格的组合证明,有一定的组合意义,而文献[5-11]是在归纳法的基础上得到的.显然我们的结论更有实际意义.
2.本文得到的结论比文献[5-11]要广,文献[5-11]中仅仅考虑了指数型矩阵对角线上的元素全为1的情况,显然更加广泛.
3.对于同样一个Hankel矩阵,能得到不同的分解,最后得到相同的结论,比如该例题中由阶乘数序列构成的Hankel矩阵还可以有下面不同的分解.

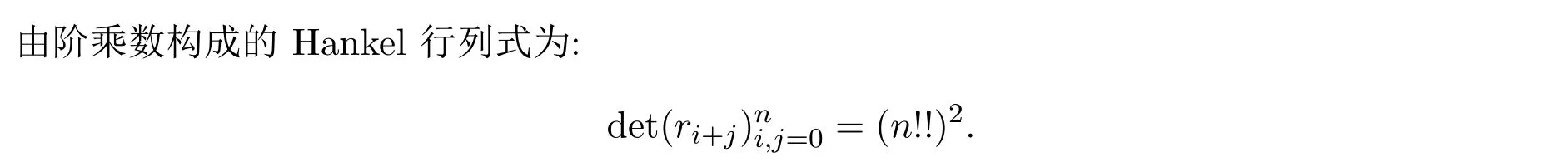
注 3.4该例题中对a取不同的值就会得到由阶乘数序列构成的Hankel矩阵的不同的分解,最后得到一致的结论.前三个例题得到的是多项式序列的Hankel行列式,本文对其中的x取特殊的值,就能得到许多的Hankel行列式的值,这在其他文献中是没有的.最后两个例题是指数型Riordan矩阵对角线上元素不全为1的具体的例子,能够具体的反映定理2.1和定理3.1的结果.
[1]Shapiro L W,Getu S,Woan W J,et al.The Riordan group[J].Discrete Applied Mathematics,1991, 34(1/3):229-239.
[2]Barry P.Constructing Exponential Riordan arrays from their A and Z sequences[J].Journal of Integer Sequences,2014,17:1-19.
[3]Deutsch E,Ferrari L,Rinaldi S.Production matrices and Riordan array[J].Annals of Combinatorics,2009,13: 65-85.
[4]Deutsch E,Ferrari L,Rinaldi S.Production matrices[J].Adv.in Appl.Math.,2005,34:101-122.
[5]Peart P,Woan W J.Generating functions via Hankel and Stieltjes matrices[J].Journal of Integer Sequences, 2000,3(2):Article 00.2.1.
[6]Aigner M.Motzkin numbers[J].European J.of Comb.,1998,19:663-675.
[7]Aigner M.Catalan-like numbers and determinants[J].J.Combin.Theory Ser,1999,87(A):33-51.
[8]Barry P.Riordan arrays,Orthogonal polynomials as moments and Hankel transforms[J].Journal of Integer Sequences,2011,14:1-37.
[9]Sivasubramanian S.Hankel determinants of some sequences of polynomials[J].Seminaire Lotharingien de Combinatoire,2010,63:1-8.
[10]Sloane N J A.The On-Line Encyclopedia of Integer Sequences[OL].published electronically at http://oeis.org,2014.
[11]Aigner M.A characterization of the Bell numbers[J].Discrete Math.,1999,205:207-210.
[12]王丽娟,杨胜良.Riordan矩阵在广义Motzkin路计数中的应用[J].纯粹数学与应用数学,2016,32(2):160-168.
The Hankel determinants of some weighted Motzkin sequences
Li Yanjun,Yang Shengliang
(School of Science,Lanzhou University of Technology,Lanzhou 730050,China)
Based on the classical Motzkin paths,a new family of weighted Motzkin paths is introduced.By means of those paths,the combinatorial interpretation of some Exponential Riordan arrays are given.Meanwhile, the addition formula of the 0 column elements of Riordan arrays,i.e.,weighted Motzkin sequences,is obtained.As an application,the evaluation of Hankel determinants of some weighted Motzkin sequences are also obtained.
exponential Riordan array,weighted Motzkin path,addition formula,Hankel determinant
O157.1
A
1008-5513(2017)01-0026-11
10.3969/j.issn.1008-5513.2017.01.004
2016-10-16.
国家自然科学基金(11561044).
李彦君(1990-),硕士生,研究方向:代数组合与组合优化.
2010 MSC:05A15,15A09.

