从知识交汇视角,落实提高学科能力
[摘 要] 在知识点交汇处命题能有效考查考生对知识的系统梳理能力、综合运用所学知识解决问题的能力,故此类试题的命制成为高考的亮点,也是必考点. 因此在平时的教学中在学生熟练掌握所学内容的基础上,教师要善于引导学生挖掘知识点之间的关联,寻找交汇的视角,提高学生分析问题、解决问题的能力,进而提高学科能力.
[关键词] 交汇;解析几何;平面几何;圆;椭圆
解析几何是高中数学的一个必考内容,由于这类问题涉及知识面广、交汇性强、思路灵活,能有效地考查学生的思维能力以及运算能力,常作为高考的压轴题或把关题,因此倍受高考命题者的青睐. 此类问题的交汇视角最常见的是与平面几何的交汇以及与函数方程的交汇等. 下面以2016年全国卷Ⅰ圆锥曲线解答题为例,就其命题特色、交汇视角、求解方法等进行分析,供读者参考.
[?] 试题赏析
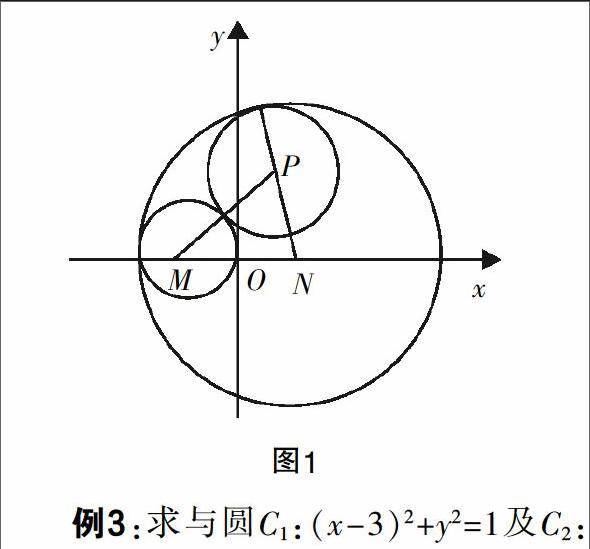
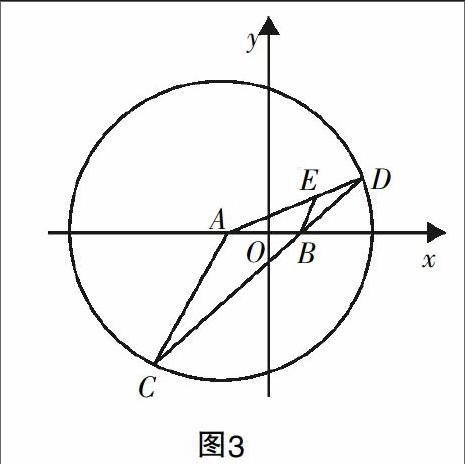
例1:(2016全国卷Ⅰ理科20)设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(1)证明EA+EB为定值,并写出点E的轨迹方程;
(2)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
近年来高考对圆锥曲线问题的常考模式:一条直线与一个圆锥曲线相交,给出直线及圆锥曲线满足的其他几何条件,如离心率、弦长、弦中点等有关条件,求圆锥曲线方程或其他相关问题.
此类问题的常用解法为:首先联立方程组,消元后利用根与系数的关系整体求解,或用“点差法”求解. 然而本题却难以直接套用,因为本题是椭圆与圆的交汇问题,需要借助平面几何中圆的相关性质来求曲线方程,接下来再按常规思路求解.
本题的一个鲜明的特点不是考查学生会不会套用常见题型的常规求解方法,重在考查的是考生会不会思维,有没有良好的思维习惯,考查的是学生那种探索、求真、质疑的良好学习习惯,加大思維量.部分学生在平时的数学学习中,眼高手低,遇到运算稍微复杂的题目,嫌麻烦,而不动笔进行具体计算,认为只要知道解题思路即可. 长此以往,运算求解能力就难以提高,一旦遇到计算复杂的问题,就会出现手忙脚乱的情形,不仅处理速度慢,而且顾此失彼,本来难度不是很大的题,却解答不出来.
[?] 分析评述
此题第(1)问是两条线段长度之和的定值问题和动点的轨迹问题,即为定值. A,B为两个定点,E为动点,从所证的结论我们已经看出了椭圆的身影,到两个定点的距离之和为定值的点的轨迹. 充分利用平面几何中圆的性质、等腰三角形的性质以及平行线的性质,不难证明|EA|+|EB|等于已知定圆的半径,当然是定值.再结合椭圆的定义,即可判断动点E的轨迹是椭圆,进而即可写出其方程.
以圆为背景对圆锥曲线定义的考查,可将问题追溯到选修2-1中,如下两例.
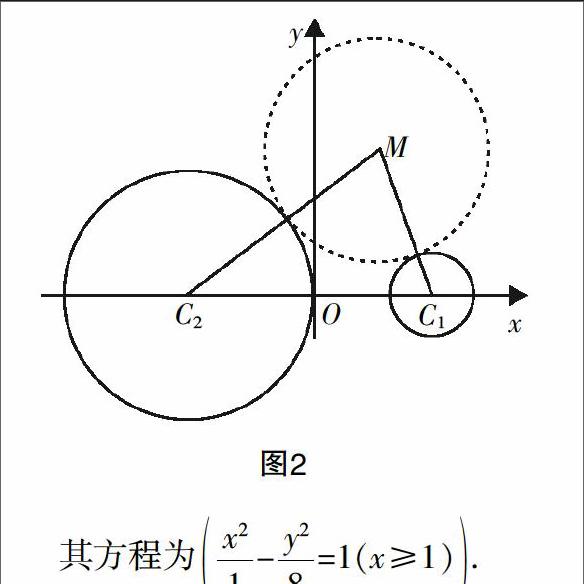
例2:已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C,求C的方程.
因为圆P与圆M外切并且与圆N内切,结合图形,不难发现
其方程为
-=1(x≥1)
.
在第(1)问得出椭圆方程后,问题就转化为我们熟悉的类型,即直线与圆锥曲线相交问题,可采用坐标法、代入消元法、差别式及根与系数的关系求解. 求解第(2)问的前提是求出四边形MPNQ的面积函数,然后确定其取值范围. 注意到这个四边形的四个顶点是由直线l与第(1)问中求出的椭圆C1的交点,以及过点B且垂直于l的直线与已知圆的交点所确定的,这自然想到应考虑直线l斜率的存在与否,所以应分“直线l与x轴不垂直”和“直线l与x轴垂直”两种情况讨论. 此外,无论是上述哪一种情况,都可以把四边形分割成两个三角形来处理. 为此需要通过弦长公式或通过圆的半径、弦心距以及半弦所构成的直角三角形,利用勾股定理求弦长,然后根据上述两种情况再确定四边形面积的取值范围.
[?] 试题解析
(1)方法1:因为
=4,所以由椭圆定义可得点E的轨迹方程为:+=1(y≠0).
(2)当直线l与x轴不垂直时,可设直线l的方程为
y=k(x-1)(k≠0),M(x1,y1),N(x2,y2).
由y=k(x-1),
=1, 可得(4k2+3)x2-8k2x+4k2-12=0,
Δ=4×36k2+4×36>0.
由韦达定理,可得x1+x2=
易求过点B(1,0)且与l垂直的直线m:y=-(x-1),从而点A到直线m的距离为,所以PQ=2=4,
故四边形MPNQ面积为S=MN·PQ=12=12,
从而当直线l与x轴不垂直时,四边形MPNQ面积的取值范围是(12,8).
当直线l与x轴垂直时,其方程为x=1,MN=3,PQ=8,四边形MPNQ的面积为12.
综上可知,四边形MPNQ面积的取值范围是[12,8).
点评:本题第(1)问依据平面几何的几何性质,利用数形结合,可简洁证明结论. 在求出椭圆的方程后注意条件y≠0的限制. 在第(2)问解答中需要注意几点:(1)对直线l的斜率存在与否要进行分类讨论;(2)注意对判别式的讨论,以便于缩小参数的取值范围;(3)直线m的方程引入时,注意直线m与l的关系,即m与l垂直,斜率互为负倒数. (4)对于
PQ
的求解,也可联立直线m与椭圆方程求解. (5)解析几何中的最值问题,最终都转化为函数最值问题处理,要熟练掌握配方法、分离常数法、均值不等式法、导数法等常用求解最值的方法.
综上,此题突出了解析几何与平面几何的交汇,具有较强的综合性,着重考查了直线与圆的位置关系、直线与椭圆的位置关系、椭圆的定义、弦长公式、平行线的性质、勾股定理、三角形面积等知识,考查了分类与整合的思想以及运算求解能力和推理论证能力. 无疑,通过这类问题求解,可以有效地检测和提高学生的数学能力.

