关于[4.8.8]铺砌中椭圆上D-点数的研究

魏祥林，王卫琪

(河北科技大学理学院，河北石家庄 050018)

关于[4.8.8]铺砌中椭圆上D-点数的研究

魏祥林，王卫琪

(河北科技大学理学院，河北石家庄 050018)

阿基米德平面铺砌是指用一种或多种正多边形铺砌全平面，且要求铺砌的每个顶点的顶点特征相同。阿基米德平面铺砌共有11种，针对其中的[4.8.8]铺砌，即每个铺砌顶点连接边长相同的一个正方形，两个正八边形，研究[4.8.8]铺砌上的椭圆所包含铺砌顶点数的特性，通过对椭圆内半弦上顶点列的分析，采用数的几何及数论中同余的方法给出顶点数的取值算法，并获得顶点数与椭圆短半轴长平方的比值的极限公式，证明极限值与对应铺砌的中心多边形的面积有关。所得算法及极限公式对其他阿基米德铺砌中相关问题的研究有借鉴作用。

离散几何；阿基米德铺砌；椭圆；中心多边形；凸包

从铺砌的定义看出，整数格即可视为由单位正方形构成的[4.4.4.4]阿基米德铺砌的顶点集。从这个意义出发，利用数的几何中讨论格点性质的相关手法探讨其他阿基米德铺砌的顶点性质成为一个有意义的研究课题。DING等[6]首次尝试将数的几何中关于整数格点的Pick定理推广至[6.6.6]铺砌的顶点集[6]，之后在相关问题研究中获得了一系列成果[7-13]。在以上研究的基础上，KOLODZIEJCZYK等[8-9，14-19]从几何的角度证明数论中一些计数问题和面积问题。本文主要研究的是由正方形和正八边形生成的[4.8.8]铺砌上的计数问题。

图1 C-点和D-点的分布Fig.1 Distribution of C-points and D-points

[4.8.8]铺砌是一种阿基米德铺砌，如图1所示。这里为了讨论的方便，记[4.8.8]铺砌的的顶点集为D，其中的点称为D-点，本文中[4.8.8]铺砌中正八边形与正方形铺砌元的边长均取为1。在[4.8.8]阿基米德铺砌中以正八边形中心为椭圆中心、以正整数n为短半轴长、2n为长半轴长的椭圆记为E(n)，E(n)的内部和边界上所含的顶点数记为N(n)。

1 基本定义

定义1 在En中，若一个集合中任意2点的直线段均含于该集合中，则称该集合为凸集。称包含一个集合的最小凸集为该集合的凸包。

定义2 在[4.8.8]阿基米德铺砌中，与一个铺砌顶点相关联的每个铺砌元的中心的凸包形成的图形称为该顶点对应的中心多边形。

2 相关引理和主要结论

本文研究[4.8.8]阿基米德铺砌中，落在椭圆E(n)的内部和边界上的顶点数N(n)的取值，给出相应的算法，并得出下述结论。

3 N(n)的取值分析

图2 椭圆弦的分布Fig.2 Distribution of the chords of the ellipse

情形1i≡0(mod 4)

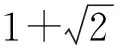
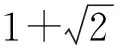
情形2i≡1(mod 4)

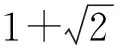
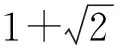
情形3i≡2(mod 4)

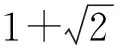
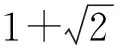
情形4i≡3(mod 4)

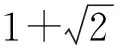
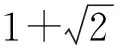
由上述讨论过程可以给出下述算法来计算[4.8.8]铺砌中椭圆E(n)的内部和边界上所含D-点的个数N(n)：

7)如果i≤k，用i+1代替i，并进行步骤2，否则，停止程序并输出N×4。

表1 部分N(n)的值

根据上述算法，运用VC++程序，对于任意给定n∈Z+可以确定N(n)的值，表1给出了部分N(n)的值。

4 定理1的证明

图3 [4.8.8]铺砌的划分Fig.3 Dividing of [4.8.8]-tiling

即

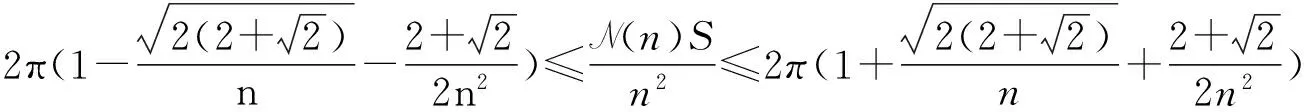
而

5 定理1的推广

经过对定理1的证明过程研究发现，在[4.8.8]铺砌中，当其他条件不变，椭圆的长半轴长为mn、短半轴长为n时，通过定理1的类似证明可以得到下述定理。

6 结 语

本文研究了在[4.8.8]阿基米德铺砌中椭圆内及其边界上的铺砌顶点数计数问题。证明了当椭圆的短半轴长为正整数n，且长半轴长与短半轴长的比值一定时，椭圆内及其边界上的总顶点数与短半轴长的平方的比值极限始终是一个常数。那么我们就不难发现，当椭圆的短半轴长为任意正数，且长半轴长与短半轴长的比值给定时，椭圆的内部或边界上的总顶点数与短半轴长的关系与定理2是相同的，相关证明可由数学分析两边夹定理推导证得。

/References：

[1] GRUBER P. Convex and Discrete Geometry [M]. New York:Springer，2007.

[2] GRUNBAUM B，SHEPHARD G C. Tilings and Patterns [M].New York:W H Freeman & Co，1986.

[3] CAO P，YUAN L. The number ofH-points in a circle [J]. Ars Combinatoria，2010，97A：311-318.

[4] WEI X，WANG J，GAO F. A note area of lattice polygons in an Archimedean tiling [J]. Journal of Applied Mathematics and Computing，2015，48(1)：573-584.

[5] 张红玉. 关于一类双铺砌顶点性质的研究 [D]. 石家庄:河北师范大学，2010. ZHANG Hongyu.Some Properties on the Vertics of a Dihedral Tiling[D].Shijiazhuang:Hebei Normal University,2010.

[6] DING R，REAY J R. The boundary characteristic and Pick’s theorem in the Archimedean planar tilings [J]. Journal of Combinatorial Theory，Series A，1987，44(1)：110-119.

[7] WEI X，DING R. On the interior lattice points of convex lattice 11-gon [J]. Journal of Applied Mathematics and Computing，2009，30(1)：193-199.

[8] DING R，KOLODZIEJCZYK K，MURPHY G，et al. A Pick-type approximation for areas ofH-polygons [J]. American Mathematical Monthly，1993，100(7)：669-673.

[9] KOLODZIEJCZYK K，OLSZEWSKA D. On some conjectures by Rabinowitz [J]. Ars Combinatoria，2006，79：171-188.

[10]DING R，REAY J R，ZHANG J R. Areas of generalizedH-polygons [J]. Journal of Combinatorial Theory，Series A，1997，77(2)：304-317.

[11]WEI X,DING R.H-triangles with 3 interiorH-points [J]. Journal of Applied Mathematics and Computing，2008，27(1/2)：117-123.

[12]WEI X,DING R.H-triangles withkinteriorH-points [J]. Discrete Mathematics，2008，308(24)：6015-6021.

[13]WEI X，DING R. Lattice polygons with two interior lattice points[J]. Mathematical Notes，2012，91(5)：868-877.

[14] KOLODZIEJCZYK K，OLSZEWSKA D. A proof of Coleman’s conjecture [J]. Discrete Mathematics，2007，307(115)：1865-1872.

[15]KOLODZIEJCZYK K. Areas of lattice figures in the planar tilings with congruent regular polygons [J]. Journal of Combinatorial Theory，Series A，1991，58(1)：115-126.

[16]KOLODZIEJCZYK K. The boundary characteristic and the volume of lattice polyhedra[J]. Discrete Mathematics，1998，190(1/2/3)：137-148.

[17]KOLODZIEJCZYK K，REAY J. Polynomials and spstial Pick-type theorems[J]. Expositiones Mathematicae，2008，26(1)：41-53.

[18]KOLODZIEJCZYK K. Parity properties and terminal points for lattice walks with steps of equal length[J]. Journal of Mathematical Analysis and Applications，2009，355(1)：363-368.

[19]KOLODZIEJCZYK K. Hex-triangles with one interiorH-points [J]. Ars Combinatoria，2004，70：33-45.

[20]OLDS C，LAX A，DAVIDOFF G. The Geometry of Numbers [M]. London:Springer London，2001.

Research about the number ofD-points of [4.8.8]-tiling in given ellipse

WEI Xianglin， WANG Weiqi

(School of Science， Hebei University of Science and Technology， Shijiazhuang， Hebei 050018， China)

An Archimedean tiling is a tiling of the plane by one type of regular polygon or several types of regular polygons, and every vertex of the tiling has the same vertex characteristics. There are 11 Archimedean tiling, and this paper studies [4.8.8]-tiling, which is an Archimedean tiling generated by squares and regular octagons in the plane, and every vertex is associated with one square and two octagons. This paper studies the number of vertices contained in an ellipse in [4.8.8]-tiling. Through analysing the sequence of vertices lying on half chord in the ellipse, and using the method of the geometry of number and congruence in number theory, it presents an algorithm about the value of the number of vertices contained in the ellipse, and obtains a formula of limit about the number of vertices and the square of short semi-axis of the ellipse. It is proved that the value of limit is connected with the area of the corresponding central polygon. The algorithm and the formula of limit are very useful for the study of related problems in other Archimedean tilings.

discrete geometry; Archimedean tiling; ellipse; central polygon; convex hull

1008-1542(2017)02-0143-08

10.7535/hbkd.2017yx02007

2016-08-12；

2017-02-01；责任编辑：张 军

河北省自然科学基金(A2014208095)

魏祥林(1974—),女，河北张家口人，教授，博士，主要从事离散与组合几何方面的研究。

E-mail:sd_wxl@126.com

O157.3 MSC(2010)主题分类：52C15

A

魏祥林，王卫琪. 关于[4.8.8]铺砌中椭圆上D-点数的研究[J].河北科技大学学报,2017,38(2):143-150.

WEI Xianglin , WANG Weiqi. Research about the number ofD-points of [4.8.8]-tiling in given ellipse[J].Journal of Hebei University of Science and Technology,2017,38(2):143-150.