插值矩阵法分析轴向受载的Euler-Bernoulli 梁双向弯曲与扭转耦合振动

张金轮, 葛仁余, 韩有民, 牛忠荣, 程长征

(1.安徽工程大学 力学重点实验室,安徽 芜湖 241000; 2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

插值矩阵法分析轴向受载的Euler-Bernoulli 梁双向弯曲与扭转耦合振动

张金轮1, 葛仁余1, 韩有民1, 牛忠荣2, 程长征2

(1.安徽工程大学 力学重点实验室,安徽 芜湖 241000; 2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

文章运用插值矩阵法研究了轴向受载的Euler-Bernoulli 梁的双向弯曲扭转耦合自由振动问题。选择梁横截面的剪切中心作为坐标原点,坐标轴平行于梁截面的几何轴,振动微分方程中有关梁截面几何特性的参数均采用相对于几何轴的参数。轴向受载的Euler-Bernoulli 梁的双向弯曲扭转耦合自由振动频率的计算转化为一组非线性常微分方程特征值问题,运用插值矩阵法求解,获得了3种边界条件下梁弯扭耦合振动的固有频率及其相应振型函数的计算结果,将数值计算结果与已有结果比较表明,文中方法具有很高的精度和效率。

Euler-Bernoulli梁;轴向荷载;固有频率;插值矩阵法

0 引 言

弯扭耦合薄壁梁在机械工程、土木工程和航天航空工程等结构工程领域的应用十分广泛,研究其弯扭耦合的固有振动和稳定性特征具有重要的实际意义。对于轴向荷载作用下梁的振动问题,相关研究大多是基于Euler-Bernoull梁理论或者Timoshenko梁理论,这些理论假定弯曲振动和扭转振动互不耦合,这样使得梁的振动计算方便可行。然而在实际工程问题中,在某些情形下梁的横截面无对称性,现有的Timoshenko梁理论和Euler-Bernoulli梁理论对这些问题均无法求解[1]。因此,有必要进行弯扭耦合梁的精确振动和稳定性分析。

近年来有研究者对轴向受载薄壁梁的弯扭耦合振动进行了研究。文献[2]采用动态传递矩阵法研究了轴向受载的Timoshenko复合材料闭合薄壁梁的弯曲扭转耦合振动,考虑了剪切变形、转动惯量的影响,忽略了翘曲刚度的影响;文献[3]运用有限元方法分析开口薄壁截面直梁在保守的静态荷载作用下的屈曲荷载,文献[4]推导出考虑翘曲剪应力的开口薄壁单元约束扭转的刚度矩阵和质量矩阵;文献[5]根据Benscoter 梁理论,用双曲函数为插值函数,建立薄壁梁约束扭转的有限元模型;文献[6]通过建立一般非对称截面薄壁杆件弯扭耦合的微分方程式,推导出了薄壁杆件单元在弯扭耦合情况下的刚度矩阵;文献[7]采用微分变换法研究了轴向受载的Timoshenko复合材料梁的弯扭耦合振动,并讨论了轴向荷载、长细比对振动特性的影响,该梁为闭口杆件;文献[8]研究了单轴对称Timoshenko复合材料破损梁的弯曲扭转耦合振动,并讨论了破损程度对振动特性的影响。

本文忽略翘曲刚度的影响,从Euler-Bernoulli梁弯-弯-扭耦合振动一般形式的微分方程组出发,将振动固有频率的计算转化为常微分方程组的特征值求解,运用插值矩阵法[9]求解常微分方程组特征值问题,获得了Euler-Bernoulli梁弯-弯-扭耦合振动所有固有频率,同时相应的振型函数一并解出。插值矩阵法原理简单、易于计算、实用性好、计算精度高,能灵活适用于任意复杂工程结构的自由振动问题。

1 轴向受载梁双向弯扭耦合振动方程

等截面匀质Euler-Bernoulli梁如图1所示,其横截面质心和剪切中心分别用C和S表示,Y轴和Z轴为通过横截面剪切中心S且平行于几何轴的坐标轴,YY轴和ZZ轴为横截面的几何轴。

质心C在YSZ坐标系中的坐标为(ey,ez);v(x,t)为梁截面剪切中心S沿Y轴方向的位移,以沿Y轴正向为正;w(x,t)为梁截面剪切中心沿Z轴方向的位移,以沿Z轴正向为正;φ(x,t)为梁截面绕剪切中心的扭转角,以沿X轴正向为正。假定轴向荷载P作用于横截面的质心,且规定压缩时为正、拉伸时为负。

图1梁的横截面示意图

轴向受载情况下梁的双向弯扭耦合振动方程[10]为:

(1)

(2)

(3)

其中,Iyy、Izz分别为梁横截面关于几何轴的惯性矩;Iyz为梁横截面关于几何轴的惯性积;GJ为横截面的扭转刚度;IS为单位长度梁关于剪切中心的极质量惯性矩;m为单位长度梁的质量。

假定v(x,t)、w(x,t)和φ(x,t)随时间正弦变化,即

(4)

(5)

(6)

(7)

由于上述常微分方程(5)～(7)式含ω2,导致问题的非线性,令

(8)

将(8)式代入(5)～(7)式可得:

(9)

(10)

(11)

一般情况下梁的3种边界情况为固定、自由以及简支。

当ξ=0,1时，简支-简支边界条件为:

(12)

当ξ=0时，固定-自由边界条件为:

(13)

当ξ=1时，固定-自由边界条件为：

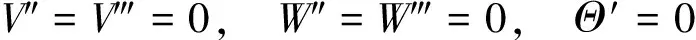
(14)

当ξ=0,1时，自由-自由边界条件为:

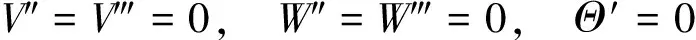
(15)

至此,轴向受载的Euler-Bernoulli梁双向弯曲与扭转耦合自由振动频率的计算,转化为求解满足边界条件 (12)～(15)式时常微分方程(8)～(11)式的特征值问题。

2 解法与算例分析

由上述途径求解轴向受载的Euler-Bernoulli梁双向弯曲与扭转耦合自由振动频率问题,需要一种有效的方法求解边界条件(12)～(15)式时常微分方程(8)～(11)式的特征值问题。根据文献[9]建立的插值矩阵法,假设一个有r个方程的线性常微分方程组特征值问题为:

(16)

其中,i=1,…,r;x∈[xa,xb]。相应的边值条件为:

(17)

其中,l=1,…,t;xa≤ξlkj≤xb。

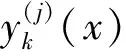
设一轴向受载的等截面匀质Euler-Bernoulli薄壁梁[10],梁材料特性参数和几何特性参数分别为:

m=21.62 kg/m,L=5 m,

ey=35.7 mm,ez=53.69 mm,

GJ=3 710 N·m2,EIyy=4 995 534 N·m2,

EIzz=385 625 N·m2,

EIyz=-433 956 N·m2,IS=0.29 N·m。

采用插值矩阵法求解常微分方程(8)～(11)式和边界条件(12)～(15)式,ξ∈[0,1]区间分段数取n=40,可获得轴向受载的等截面匀质Euler-Bernoulli薄壁梁双向弯曲和扭转耦合的固有振动频率。

当在薄壁梁的质心处作用轴向荷载P为0、1 500、2 500 N时,在(12)～(15)式边界条件下计算得到梁的前6阶固有频率,见表1～表3所列。由表1～表3可以看出,利用本文方法所得结果与文献[10]计算结果非常吻合,表明本文方法是有效的,且具有很高的计算精度。

薄壁梁的质心处作用轴向荷载P为0、-2 000、2 000 N时,在 (12)～(15) 式边界条件下计算得到梁的前6阶固有频率见表4所列。由表4可以看出,轴向压力的存在使得梁的固有频率趋于减小,轴向拉力使梁的固有频率趋于增大,轴力对第1阶频率的影响最大,对高阶频率的影响逐渐减小。表1～表4中的数值均已无量纲化处理。

轴向荷载P=2 500 N时简支-简支梁、固定-自由梁、自由-自由梁的前2阶固有频率对应的振型函数如图2～图4所列。

表1 轴向受拉Euler-Bernoulli简支-简支梁3种荷载下前6阶固有频率对比

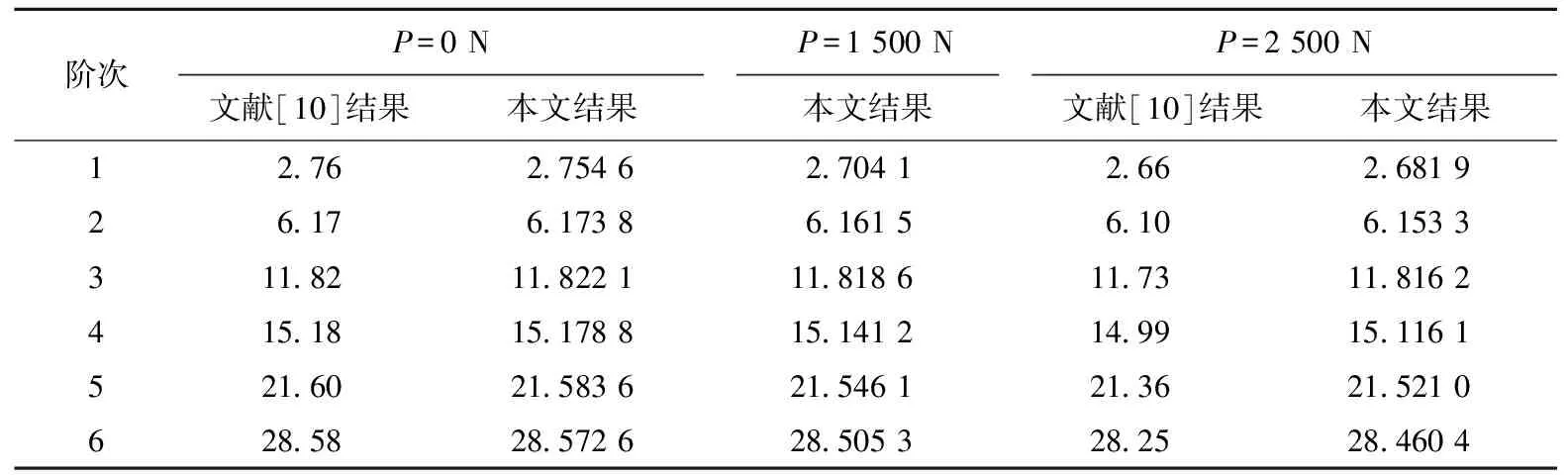
表2 轴向受拉Euler-Bernoulli固定-自由梁3种荷载下前6阶固有频率对比

表3 轴向受拉Euler-Bernoulli自由-自由梁3种荷载下前6阶固有频率对比

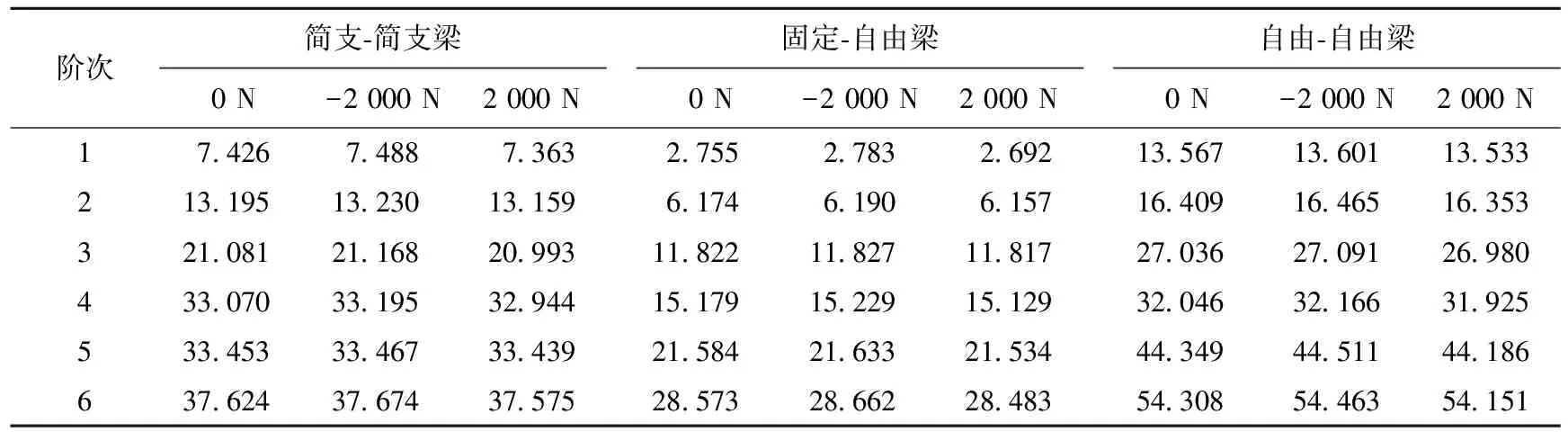
表4 轴向受拉与受压的Euler-Bernoulli梁3种荷载下前6阶固有频率本文计算结果

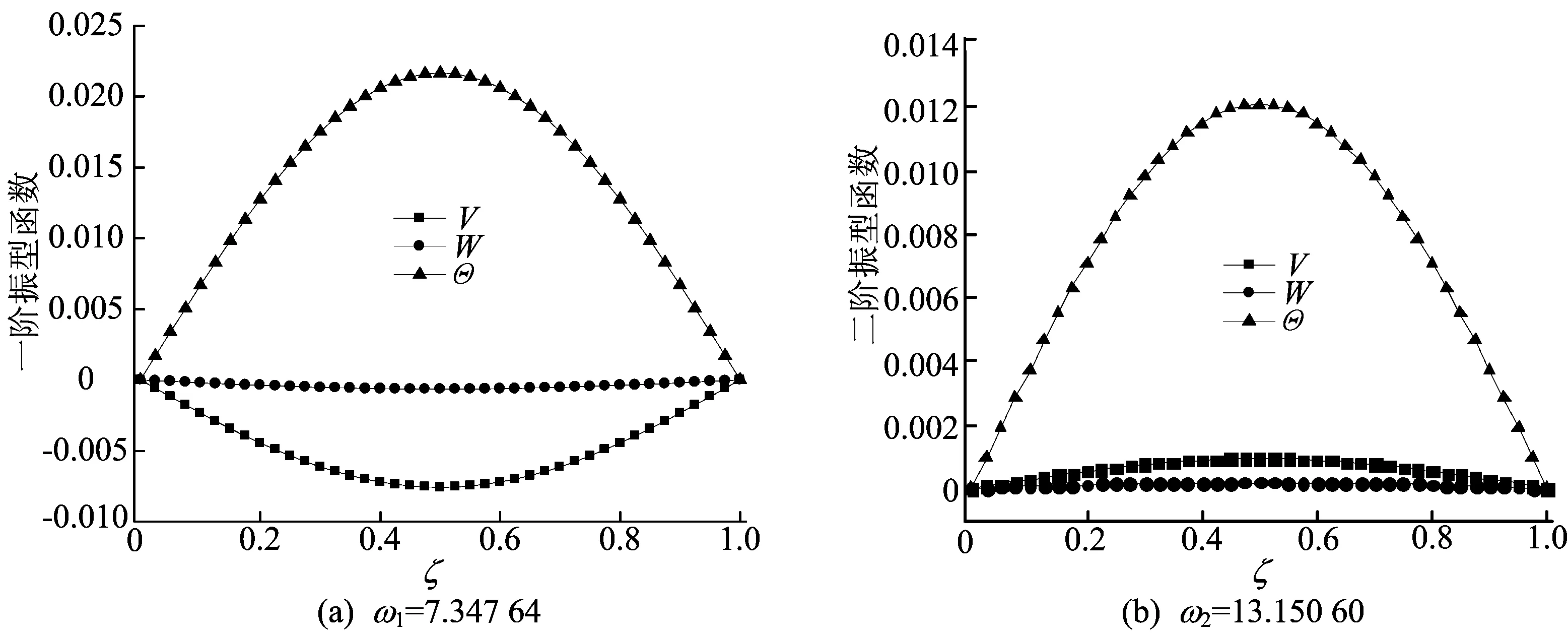
图2 P=2 500 N简支-简支梁前2阶固有频率对应的振型

图3 P=2 500 N固定-自由梁前2阶固有频率对应的振型

图4 P=2 500 N自由-自由梁前2阶固有频率对应的振型

3 结 论

本文运用插值矩阵法研究了轴向受载的Euler-Bernoulli 梁双向弯曲扭转耦合自由振动问题。选择梁横截面的剪切中心作为坐标原点,坐标轴平行于梁截面的几何轴;振动微分方程中有关梁截面几何特性的参数均采用相对于几何轴的参数。结合具体的边界条件获得自由振动微分方程,将轴向受载的Euler-Bernoulli 梁双向弯曲扭转耦合自由振动固有频率的计算转化为求解一组线性常微分方程的特征值问题。数值结果验证了本文方法在其适用范围内的精确性和有效性。主要结论如下:

(1) 插值矩阵法求解轴向受载的Euler-Bernoulli 梁双向弯曲扭转耦合自由振动问题时,可以避免用迭代法求解超越方程,可一次性解出所有的弯曲扭转耦合自由振动固有频率及其相应的振型函数。

(2) 利用本文方法所得结果与已有文献计算结果非常吻合,表明本文插值矩阵法计算梁的双向弯曲扭转耦合自由振动问题是有效的且有很高的计算精度,具有一定的工程应用价值。

(3) 轴向压力的存在使得梁的固有频率趋于减小,轴向拉力使梁的固有频率趋于增大,轴力对第1阶频率的影响最大,对高阶频率的影响逐渐减小。

[1] 黄君毅,王勇.Bernoulli-Euler 薄壁梁双向弯曲与扭转耦合的振动分析[C]//第十三届全国工程建设计算机应用学术会议论文集.[S.l.:s.n.],2006:85-91.

[2] BANERJEE J R.Free vibration of axially loaded composite Timoshenko beams using the dynamic stiffness matrix method [J].Computers and Structures,1998,69(2):197-208.

[3] LAUDIERO F,ZACCARIA D.Finite element analysis of stability of thin-walled beams of open section [J].International Journal of Mechanical Sciences,1988,30(8):543-557.

[4] ONU G.Inclusion of warping shear effect in the thin-walled core element for multistory building [J].Computers and Structures,1990,35(2):175-182.

[5] SHAKOURZADEH H,GUO Y Q,BATOZ J L.A torsion bending element for thin-walled beams with open and closed cross sections [J].Computers and Structures,1995,55(6):1045-1054.

[6] HU Yuren,JIN Xianding,CHEN Bozhen.A finite element model for static and dynamic analysis of thin-walled beams with asymmetric cross-sections [J].Computers and Structures,1996,61(5):897-908.

[7] KAYA M O,OZGUMUS O O.Flexural-torsional coupled vibration analysis of axially loaded closed-section composite Timoshenko beam by using DTM [J].Journal of Sound and Vibration,2007,306(3/4/5):495-506.

[8] VIOLA E,RICCI P,ALIABADI M H.Free vibration analysis of axially loaded cracked Timoshenko beam structures using the dynamic stiffness method [J].Journal of Sound and Vibration,2007,304(1/2):124-153.

[9] NIU Z R.Interpolating matrix method for multi-point BVPs and its error analysis [J].Chinese Journal of Computational Physics,1993,10(3):336-344.

[10] 张方,王国砚.轴向受载的Euler-Bernoulli梁的双向弯曲扭转耦合振动研究[J].力学季刊,2009,30(2):311-316.

(责任编辑 张淑艳)

Analysis of bi-axes bending-torsional coupled vibration of Euler-Bernoulli beams under axial load by interpolating matrix method

ZHANG Jinlun1, GE Renyu1, HAN Youmin1, NIU Zhongrong2, CHENG Changzheng2

(1.Key Laboratory for Mechanics, Anhui Polytechnic University, Wuhu 241000, China; 2.School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

The bi-axes bending-torsional coupled free vibrations of axially loaded Euler-Bernoulli beams with bi-asymmetric cross sections are studied by the interpolating matrix method. The reference point coincident with shear center of the beam is chosen and the reference axes are parallel to the geometric axes of cross sections. The geometric parameters of the cross sections of the beam are determined with respect to geometric axes. Then the governing equations of the free vibrations of axially loaded Euler-Bernoulli beams are transformed into a set of nonlinear characteristic ordinary differential equations(ODEs) with the natural frequencies orders. The interpolating matrix method is introduced to solve the derivative ODEs with three kinds of boundary conditions. Then the natural frequencies and the associated mode shape of the beam are obtained. The numerical results show that the method is efficient and has very high accuracy while comparing with the existing solutions.

Euler-Bernoulli beam; axial load; natural frequency; interpolating matrix method

2015-07-20；

2016-12-27

国家自然科学基金资助项目(11272111;11372094);安徽省高等学校自然科学研究重点资助项目(KJ2016A055)

张金轮(1984-),男,安徽合肥人,安徽工程大学讲师; 牛忠荣(1957-),男,安徽合肥人,博士,合肥工业大学教授,博士生导师; 程长征(1979-),男,安徽合肥人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2017.03.016

O326;TU323.3

A

1003-5060(2017)03-0373-06