嵌套抽样算法用于地下水模型评价的算例研究
曹彤彤,曾献奎,吴吉春
(南京大学地球科学与工程学院/表生地球化学教育部重点实验室,江苏 南京 210023)
嵌套抽样算法用于地下水模型评价的算例研究
曹彤彤,曾献奎,吴吉春
(南京大学地球科学与工程学院/表生地球化学教育部重点实验室,江苏 南京 210023)
模型评价(模型选择)是地下水数值模拟不确定分析的重要研究内容,模型边缘似然值是进行模型评价的重要依据。嵌套抽样算法是一种高效的高维积分计算方法,能有效计算复杂模型的边缘似然值。本次研究提出了一种基于Adaptive Metropolis的嵌套抽样算法,通过对两个(线性、非线性)解析函数及一组不同结构的地下水模型边缘似然值的计算,并与大样本条件下算术平均方法的计算结果相对比,验证了该方法对于计算模型边缘似然值的有效性。
嵌套抽样算法;模型评价;模型选择;地下水流模型;边缘似然值
近年来,数值模拟技术已成为地下水研究领域中一种不可或缺的方法,对于水资源评价、开发、管理与保护、地下水污染防治等问题具有重要意义[1]。受制于地下水系统自身的复杂性和人类认知的局限性,地下水模型的模拟结果与真实结果往往存在偏差,通常将这种差异归结为地下水模拟的不确定性[2]。按照不确定性的来源,可以分为参数、模型结构(概念模型)和观测资料的不确定性[3]。
贝叶斯推理作为一种有效概率分析理论,已广泛用于地下水模型参数和概念模型不确定性分析[4]。在贝叶斯分析框架内,通常根据观测资料(如钻孔数据、物探数据等)建立一组可行的概念模型,分别针对各概念模型进行参数不确定性分析,计算模型的边缘似然值(或称贝叶斯证据、综合似然值)[5~10]。边缘似然值是评价模型表现或计算模型权重的重要依据,然而模型的边缘似然值是其似然函数在复杂空间内的高维积分,直接计算十分困难,通常采用算术平均或基于马尔可夫链蒙特卡洛(MCMC)的调和平均进行间接数值计算[11]。算术平均方法在参数先验分布空间内随机抽样,收敛速度慢且得到的边缘概率值偏小。调和平均方法利用参数的后验分布,计算稳定性差且容易高估边缘似然值。有些学者[12~13]试图将两种方法相结合,即在参数先验分布和后验分布中混合抽样,但是在混合中又引入了新的不确定性,如混合系数等。
John Skilling[5]提出了一种计算边缘似然值的新方法——嵌套抽样算法(Nested Sampling Algorithm)。该方法基于贝叶斯理论,其核心是将复杂的高维积分转化为便于数值计算的一维积分。不同于算术平均或调和平均方法仅在先验或后验概率空间内抽样,也不是简单地将先验与后验空间混合,嵌套抽样法在抽样过程中由先验空间逐步过渡到后验空间,从而有效降低了从单一分布抽样引起的边缘似然值估计误差。嵌套抽样算法可以看作一种全局优化算法,因为其利用的有效参数集遍历了整个先验分布及后验分布。目前,嵌套抽样方法已经在水文模型中得到应用,如Elsheikh等[6]将嵌套抽样算法应用于地下水流模型的评价与不确定性分析,验证了嵌套抽样算法的收敛性和高效性,随后Elsheikh等[7~9]对嵌套抽样算法中有效集的迭代演化过程进行优化,引入非嵌入式随机多项式混沌方法(Non-intrusive Polynomial Choas)、混合蒙特卡洛方法(Hybrid Monte Carlo)、多点统计学方法(Multipoint Statistics)等提高了抽样精度和效率。Liu (2016)等[10]对嵌套抽样算法中的Metropolis-Hasting算法进行改进,分别应用于线性、非线性函数的边缘似然值的计算,并与算术平均、调和平均及热力学积分(Thermodynamic Integration)方法的计算结果对比,验证了改进后的嵌套抽样算法的计算精度与效率。
本文尝试将Adaptive Metropolis算法应用于嵌套抽样算法有效集的迭代更新,拟提高抽样效率与精度。其次,通过两个简单的解析函数验证该方法的准确性、收敛性及稳定性。最后,基于一个地下水流模型案例分析展示嵌套抽样算法在地下水模型评价中的应用。
1 理论和方法
1.1 贝叶斯理论
贝叶斯理论是不确定性分析与模型评价(或模型选择)的基础[5],对于一系列的模型Mk,k=1, 2,…,K,根据已有的数据D,相应的模型参数θ后验分布p(θ|D,Mk)可表示为:
(1)
式中:p(θ|D,Mk)——参数θ的先验概率分布; p(D|θ,Mk)——参数θ的似然函数; p(D|Mk)——模型Mk的边缘似然值。
边缘似然值(Zk)是模型Mk中似然函数在先验概率分布下的期望,通常用于评价模型表现或估计模型权重,其数学表达式为:
(2)
基于贝叶斯理论,模型的后验概率(或后验权重)p(Mk|D)定义为:
(3)
式中:p(Mk)——模型Mk的先验概率分布(先验权重)。
p(Mk|D)通常用于贝叶斯模型平均(BayesianModelAverage)。
1.2 嵌套抽样算法理论
通过积分变换,边缘似然值Zk的数学表达式(2)可以转换为[5]:
(4)
式中,L(θ|D,Mk)=p(D|θ,Mk)表示联合似然函数,dX=p(θ|Mk)dθ是先验分布累积(cumulativepriormass)的微分。定义先验分布累积为:
(5)
式(5)中X的取值范围为0≤X≤1,随着λ值的增加,即对联合似然函数的约束变强,使得满足条件L(θ|D,Mk)>λ的参数值θ越来越少,即参数空间由先验分布p(θ|Mk)逐步过渡至后验分布p(θ|D,Mk)。若X(λ)的逆向函数p(D|X,Mk)满足p(D|X(λ),Mk)= λ,将该逆向函数代入公式(4)中得到一维积分:
(6)
式(6)即为嵌套抽样方法的核心,将公式(2)中关于θ的多元高维积分转化为关于X的单变量一维积分,这相当于将多维参数空间投影到关于变量X的坐标轴上。式(6)中一维积分的数值积分累加形式可表示为:
(7)
式中:N——离散值Xi的总个数; wi——关于Xi的权重,可用向前差分的形式表示wi=Xi-1-Xi。
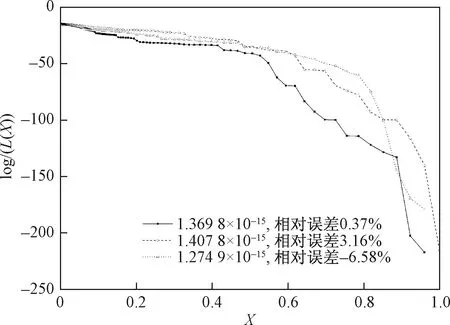
将Xi按下标递减的顺序排列成0 (8) 1.3 嵌套抽样算法的计算步骤 嵌套抽样算法可以分为嵌套抽样主算法和局部限制抽样子算法(Constrainedlocalsampling)两部分,主算法通过有效集迭代更新的方式实现公式(6)~ (8),局部限制抽样负责生成每次迭代过程所需的L~X样本。局部限制抽样通常基于概率抽样方法,如Metropolis-Hasting(MH)算法[14]等。Liu等[10]在MH算法基础上进行了3处改进,以提高计算结果的效率和准确性。本文在嵌套抽样算法的理论框架内,采用AdaptiveMetropolis(AM)算法[15]来处理局部限制抽样问题,较传统的MH算法能更好地处理复杂非线性问题。主算法的流程图如图1所示,具体步骤如下。 图1 嵌套抽样主算法流程图Fig.1 Flowchart of main algorithm of nested sampling (1) 定义参数服从的先验分布及有效集(activeset)中样本的个数N,有效集是从先验分布中随机生成参数向量θ的集合S={θ1,θ2,…θN}。计算关于每个样本的联合似然函数,将最小的联合似然函数Lworst值作为公式(5)中的λ。 开始R次迭代的第i (i=1,…, R)次循环: (2) 对于第i次循环,计算有效集S中的最小值θworst和Lworst,令Li=Lworst,根据公式(8)计算Xi,根据公式(7)计算Zi=Zi-1+wiLi(Z0=0)。 (3) 通过局部限制抽样从参数先验分布中生成新样本θnew,若L(θnew|D,M)>Lworst,则用θnew取代有效集S中的样本θworst;否则,继续从局部限制抽样算法中生成新样本θnew,直至满足L(θnew|D,M)>Lworst或达到人为定义的抽样次数上限为止。 局部限制抽样的步骤如下: (1) 从有效集S中随机选择某一参数向量θl作为φ0。开始H次迭代的第j(j=1, …,H)次循环,H是AM算法迭代的最大次数。 (2) 从正态分布N(φj-1,Cj)中生成新样本ξ,计算对应的联合似然函数值Lξ。φj(j=1,2,…,H)是生成的长度为H的马尔可夫链,Cj为协方差矩阵,在T0次迭代前取固定值C0,之后自适应更新协方差矩阵计算公式如下: (9) Cov(φ0, …, φj-1)为已有的所有样本向量的协方差矩阵。为方便计算,可以通过递归公式计算Cj+1: (10) (4) 从均匀分布U(0, 1)中随机生成u,比较u与α的大小;若u≤α则接受φj==ξ,否则φj=φj-1。 (5) 重复以上(2) ~ (4),直至生成长度为H的马尔可夫链为止;令θnew=φH。 首先,基于线性与非线性解析函数,分别应用基于MH、AM的嵌套抽样算法(NSE-MH、NSE-AM)进行案例分析。其次,基于一个理想地下水流模型,建立4个不同结构的概念模型,说明该算法在地下水数值模拟的模型选择与评价中的应用。此外,针对地下水模型,为验证嵌套抽样算法的准确性,将大样本条件下算术平均方法(ArithmeticMeanEstimator,AME)计算得到的边缘似然值作为参考值。 2.1 解析函数 (1) 线性解析函数 定义如下形式的线性解析函数: (11) 式中:x——自变量; y——因变量;a,b——常数,a=1,b=-5。 (12) 式中:C——协方差矩阵,通常为单位矩阵Id;N——监测值和样本值的个数,本例中n=20。 本例中NSE-AM参数取值为:N=25,R=250,H=100,T0=20。为验证计算结果的准确性,同时采用算术平均方法及NSE-MH进行计算,前者使用样本数量为2千万次,后者参数取值为:N=25,R=250,局部限制抽样算法中生成的马尔可夫链长为100。嵌套抽样算法和算术平均方法各运行50次,分别从50次运行中挑选出最终结果与解析解最为接近的一次,根据以上方法的抽样过程绘制边缘似然值随抽样次数的变化趋势图(图2)。从图2中可以看出,在算法收敛性的比较中,嵌套抽样算法计算的边缘似然值随抽样次数的增加而增加,NSE-AM在抽样次数达到2万次后达到稳定,且与解析解较为接近,NSE-MH在抽样次数达到20万次后达到稳定,而算术平均方法在抽样过程的前期波动较大,直到50万次后才趋于稳定,说明嵌套抽样算法的计算效率高且收敛速度快。图3是分别利用嵌套抽样算法和算术平均方法独立运行50次的计算结果绘制得到的箱形图,从图3中可以看出,算术平均方法运行结果之间相差较小,而嵌套抽样算法每次运行的结果以解析解为中心上下浮动,少数情况下存在较大的误差,这说明嵌套抽样算法在稳定性上比算术平均方法差。此外,NSE-AM在收敛速度、计算精度与稳定性方面比NSE-MH有了明显提高。 图2 线性函数的抽样过程Fig.2 Sampling process of linear function 图3 线性函数边缘似然值的箱形图Fig.3 Boxplot of marginal likelihood of linear function (2) 非线性解析函数 定义如下形式的非线性解析函数: (13) 式中:x——自变量; y——因变量;c,d——常数,c=2,d=-3。 从x={1,2,…,20}中生成20个y的样本值,在样本值加入高斯白噪声(平均值为0,方差为1)后作为监测值μ。两个参数的先验分布为c~N(2, 1)和d~N(-3, 1),生成的新样本值为Y,联合似然函数L(θ|D,Mk)同样是多维正态分布,与公式(12)相同。非线性解析函数中嵌套抽样算法和算术平均方法的参数取值和运行次数与线性解析函数相同。同理得到抽样次数和边缘似然值的关系图(图4)及每次运行结果统计得到的箱形图(图5)。从图4和图5中可以得到与图2和图3相似的结论。从图3和图5的结果可以看出,嵌套抽样算法在计算非线性函数边缘似然值时50次独立计算结果的平均值(中位数)与解析解的偏差要大于线性情况下的偏差。此外,对于非线性函数而言,基于AM的嵌套抽样算法(NSE-AM)要比基于MH的嵌套抽样算法(NSE-MH)的计算结果更为准确。 图4 非线性函数的抽样过程Fig.4 Sampling process of nonlinear function 图5 非线性函数边缘似然值的箱形图Fig.5 Boxplot of marginal likelihood of nonlinear function 2.2 地下水流模型 本次研究对象为一个三维稳定流地下水流模型,该模型在Rojas等[4]和Zeng等[16]的研究基础上建立,研究区示意图如图6所示,为一矩形含水层,东西长为5 000m,南北宽为3 000m,均匀剖分为25m×25m的网格。含水层总厚度为60m,进一步划分为3个子含水层,从上至下依次为潜水含水层、弱透水层和承压含水层,厚度分别为35m、5m和20m。渗透系数K具有非均质性,假定各层渗透系数场都符合平稳分布条件,渗透系数随机场可用各向同性的指数方差模型描述,相关长度为200m,渗透系数K的对数(lgK)的方差为1.0。各层渗透系数平均值依次为1.0m/d、0.1m/d和5.0m/d。基于地质统计学软件库(GSLIB)的序贯高斯模拟(SGSIM)[17]生成每层的渗透系数场。此外,含水层水平方向渗透系数是垂向渗透系数的10倍。 图6 研究区平面示意图Fig.6 Sketch map of the study area 研究区东侧为一河流边界,仅切穿潜水含水层,河水位35m,河床底板高程30m,河床水力传导系数20m2/d;西侧为一定水头边界,水位56m。仅有表层接受大气降水的均匀补给,降水量9.0×10-4m/d,入渗补给系数0.15。区内共有5口抽水井,总抽水量1 250m3/d(每口井的抽水量均为250m3/d)。右侧有一排水渠,渠道底板高程45m,渠的水力传导系数20m2/d。此外,研究区的南部、北部和底部均为隔水边界。地下水流模型基于MODFLOW-2005[18]建立,区内共有32口地下水位监测井(第1层和第3层中各16口)。水位的模拟值加入高斯白噪声(平均值为0,方差为0.01)后作为监测井的观测值。 图7 地下水流模型的抽样过程Fig.7 Sampling process of groundwater flow models 本次研究采用4个结构不同的概念模型(M1,M2、M3和M4)作为对未知地下水系统的近似。该模型结构的不确定性主要体现为对中间弱透水层的刻画,因为在实际水文地质调查中往往很难查明弱透水层的位置及厚度,而弱透水层又对地下水系统的模拟结果有很大的影响。4个概念模型的空间大小与真实情况完全相同(5 000m×3 000m×60m)。模型M1假设含水层只有1层,为潜水含水层,此时所有的抽水井和观测井均视为在同一层内。模型M2假设有2个含水层,即只考虑真实情况下的第一含水层和第三含水层,厚度分别为35m和25m。模型M3,M4的结构与真实情况相同,M3中含水层的厚度分别为35,3和22m;M4含水层的厚度分别为35,7和18m。 本次研究5个水文地质参数,分别为第一层的入渗补给系数、定水头边界水头、河床水力传导系数、第一层的渗透系数随机场的方差和相关长度。其他模型边界条件与真实模型相同。5个参数的先验信息均为均匀分布,其取值范围见表1。此外,第一层中有120个渗透系数观测点,观测值加上3%的高斯白噪声作为每个概念模型渗透系数随机场的输入数据。 表1 地下水流模型中参数的取值范围 由于地下水流模型具有非线性的特征,解析解不易直接求出,因此在抽样次数足够大的前提下,可将算术平均方法计算的边缘似然值作为参考值。因而本次案例分析中算术平均方法的样本数量为50万,分别计算4个模型的边缘似然值,作为对应的参考值。前面2个解析函数算例的结果说明基于AM的嵌套抽样算法(NSE-AM)的表现明显优于基于MH的嵌套抽样算法(NSE-MH),因此本例采用NSE-AM,其参数取值为:N=25,R=250,H=100,T0=20,对4个模型各进行似然值估计10次。由于嵌套抽样算法的各次计算结果不尽相同,本次研究中取10次计算结果的平均值作为最终结果,从而评价嵌套抽样算的综合表现。根据两种方法的迭代过程绘制边缘似然值随抽样次数的变化趋势图(图7),两种方法收敛后计算得到的边缘似然值见表2。假定各个概念模型的先验概率分布为均匀分布,可根据式(3)计算各个概念模型的后验概率(权重),以表2中2种方法计算得到的边缘似然值作为式(3)中的Zk,计算模型的后验概率(权重)见表3。p(Mk|D)AME表示算术平均方法计算的后验概率,p(Mk|D)NSE表示嵌套抽样算法计算的后验概率。 表2 2种方法计算水流模型的边缘似然值 表3 2种方法计算概念模型的后验概率(权重) 从中可以得到以下结论:(1) 嵌套抽样算法的结果准确、计算效率高,算术平均方法通常需要数十万次的样本数量(即地下水流模型的运行次数)才能达到稳定,需要较长的计算时间,而嵌套抽样算法经过大约2万次的模型运行即收敛,且最终得到的结果与算术平均方法较为接近。(2) 嵌套抽样算法的适应性好,对于不同的概念模型都能在有限的模型运行次数中达到稳定,而算术平均方法对于个别与真实情况相差较大的模型,如M1经过50万次模型运行也未达到稳定,而嵌套抽样算法在2万次模型运行后基本达到稳定。(3) 根据4个模型计算得到的边缘似然值及后验概率(权重),从小到大的顺序依次为:M1 为分析嵌套抽样算法各次计算结果之间存在的差异性,选取M3的3次计算过程进行研究,绘制先验分布累积X与似然函数值的自然对数lg(L(X))的关系图(图8)。可知,在嵌套抽样的前期,各次嵌套抽样过程在同一X处得到的似然函数值变化幅度较大;后期,随着X的减小,各次嵌套抽样过程得到的似然函数值变化幅度变小。根据式(8),嵌套抽样的前期具有较大的ΔX(即Xi-1-Xi),通过式(7)计算边缘似然值时,嵌套抽样初期不稳定的似然函数值L将导致边缘似然值计算结果的差异性。这与嵌套抽样算法由低概率区域快速逼近至高概率区域的抽样轨迹有关。由于随机抽样过程,每次抽样轨迹并不能确保完全一致,这导致嵌套抽样算法相对较差的稳定性。因此,为提高嵌套抽样算法的准确性与稳定性,一方面可以通过增加有效集样本的个数,即增加N来降低嵌套抽样的前期迭代步长(ΔX),但这将导致计算成本的增加[10];另一方面,使用更为高效稳定的局部限制抽样算法,如MT-DREAMzs等[19~20],以获得更加准确可靠的似然函数值L样本,从而提高模型边缘似然值计算结果的准确性和稳定性,这将是今后的研究内容之一。 图8 嵌套抽样算法中边缘似然值的计算过程(M3)Fig.8 Calculation process of marginal likelihood of nested sampling algorithm(M3) (1) 将模型边缘似然值作为评价模型表现的依据,采用基于AM的嵌套抽样算法计算模型边缘似然值,通过对两个(线性、非线性)解析函数及一组不同结构的地下水模型边缘似然值的计算与验证,为模型评价(模型选择)提供了依据。将嵌套抽样算法的结果与大样本条件下算术平均方法的计算结果对比,4个地下水概念模型边缘似然值的计算误差分别为-6.86%、-2.16%、3.27%和-0.94%,说明嵌套抽样算法具有准确性较高、计算效率高、收敛速度快等优点,具有较大的发展潜力。考虑模型的参数不确定性,嵌套抽样算法能够有效计算不同结构(不同复杂程度)模型的边缘似然值,说明该方法有良好的稳定性与适用性。 (2) 尽管基于AM的嵌套抽样算法在准确性、收敛性和稳定性上较基于MH的嵌套抽样算法有所提高,但是在计算的稳定性上还值得进一步改进,使用基于MT-DREAMzs的嵌套抽样算法提高模型边缘似然值计算结果的准确性和稳定性,将是今后的研究内容之一。此外,本次研究省略了对模型和参数后验分布的研究,而模型和参数的识别问题在实际工作中十分重要。因此,下一步的工作中,拟重点针对模型和参数的后验分布展开深入研究。 [1] 陆乐, 吴吉春, 王晶晶. 多尺度非均质多孔介质中溶质运移的蒙特卡罗模拟[J]. 水科学进展, 2008, 19(3): 333-338.[LU L, WU J C. WANG J J. Monte Carlo modeling of solute transport in a porous medium with multi-scale heterogeneity[J]. Advances in Water Science, 2008, 19(3): 333-338. (in Chinese)] [2] 吴吉春, 陆乐. 地下水模拟不确定性分析[J]. 南京大学学报(自然科学版), 2011, 47(3): 227-234. [WU J C, LU L. Uncertainty analysis for groundwater modeling[J]. Journal of Nanjing University (Natural Science), 2011, 47(3): 227-234. (in Chinese)] [3] Hassan A E, Bekhit H M, Chapman J B. Uncertainty assessment of a stochastic groundwater flow model using GLUE analysis[J]. Journal of Hydrology, 2008, 362(1): 89-109. [4] Rojas R, Feyen L, Dassargues A. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging[J]. Water Resources Research, 2008, 44(12): W12418. [5] Skilling J. Nested sampling for general Bayesian computation[J]. Bayesian analysis, 2006, 1(4): 833-859. [6] Elsheikh A H, Wheeler M F, Hoteit I. Nested sampling algorithm for subsurface flow model selection, uncertainty quantification, and nonlinear calibration[J]. Water Resources Research, 2013, 49(12): 8383-8399. [7] Elsheikh A H, Hoteit I, Wheeler M F. Efficient Bayesian inference of subsurface flow models using nested sampling and sparse polynomial chaos surrogates[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 269: 515-537. [8] Elsheikh A H, Wheeler M F, Hoteit I. Hybrid nested sampling algorithm for Bayesian model selection applied to inverse subsurface flow problems[J]. Journal of Computational Physics, 2014, 258: 319-337. [9] Elsheikh A H, Demyanov V, Tavakoli R,etal. Calibration of channelized subsurface flow models using nested sampling and soft probabilities[J]. Advances in Water Resources, 2015, 75: 14-30. [10] Liu P, Elshall A S, Ye M,etal. Evaluating marginal likelihood with thermodynamic integration method and comparison with several other numerical methods[J]. Water Resources Research, 2016, 52(2): 734-758. [11] Kass R E, Raftery A E. Bayes factors[J]. Journal of the american statistical association, 1995, 90(430): 773-795. [12] Newton M A, Raftery A E. Approximate Bayesian inference with the weighted likelihood bootstrap[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1994, 56(1): 3-48. [13] Marshall L, Nott D, Sharma A. Hydrological model selection: A Bayesian alternative[J]. Water resources research, 2005, 41(10): W10422. [14] Chib S, Greenberg E. Understanding the Metropolis-Hastings algorithm[J]. The American Statistician, 1995, 49(4): 327-335. [15] Haario H, Saksman E, Tamminen J. An adaptive Metropolis algorithm[J]. Bernoulli, 2001, 7(2): 223-242. [16] Zeng X, Ye M, Burkardt J,etal. Evaluating two sparse grid surrogates and two adaptation criteria for groundwater Bayesian uncertainty quantification[J]. Journal of Hydrology, 2016, 535: 120-134. [17] Deutsch C V, Journel A G. Geostatistical software library and user’s guide[J]. Oxford University Press, New York, 1998. [18] Harbaugh A W. MODFLOW-2005, the US Geological Survey modular ground-water model: the ground-water flow process[M]. Reston, VA, USA: US Department of the Interior, US Geological Survey, 2005. [19] Andrieu C, Moulines é. On the ergodicity properties of some adaptive MCMC algorithms[J]. The Annals of Applied Probability, 2006, 16(3): 1462-1505. [20] Vrugt J A, Ter Braak C J. DREAM (D): an adaptive Markov Chain Monte Carlo simulation algorithm to solve discrete, noncontinuous, and combinatorial posterior parameter estimation problems[J]. Hydrology and Earth System Sciences, 2011, 15(12): 3701-3713. Application of nested sampling algorithm for assessing the uncertainty in groundwater flow model CAO Tongtong, ZENG Xiankui, WU Jichun (KeyLaboratoryofSurficialGeochemistryMinistryofEducation/SchoolofEarthSciencesandEngineering,NanjingUniversity,Nanjing,Jiangsu210023,China) The model evaluation (model selection) is an important research content of uncertainty analysis of groundwater numerical simulation, and marginal likelihood of a model is an essential basis for model evaluation. Nested sampling algorithm is an efficient high-dimensional integral method, which can effectively calculate the marginal likelihood of complex model. The nested sampling algorithm based on Adaptive Metropolis was proposed in this study, by calculating the marginal likelihoods of two (linear, non-linear) analytic functions and a set of groundwater models with different structures, and compared with the results of the arithmetic average method under the condition of large sample, the validity of the method was verified. The results show that the nested sampling algorithm has high calculation accuracy and computational efficiency, and is an effective model evaluation method. nested sampling algorithm; model evaluation; model selection; groundwater flow model; marginal likelihood 10.16030/j.cnki.issn.1000-3665.2017.02.11 2016-10-08; 2017-01-16 国家自然科学基金项目资助(41302181; 41172207; 51190091);国家重点研发计划“水资源高效开发利用”重点专项项目资助(2016YFC0402802) 曹彤彤(1993-),女,研究生,水文学及水资源专业。E-mail: caotong1993@yeah.net 曾献奎(1985-),男,副研究员,从事地下水数值模拟研究。E-mail: zengxiankui@yeah.net P641.2 A 1000-3665(2017)02-0069-08





2 算例分析


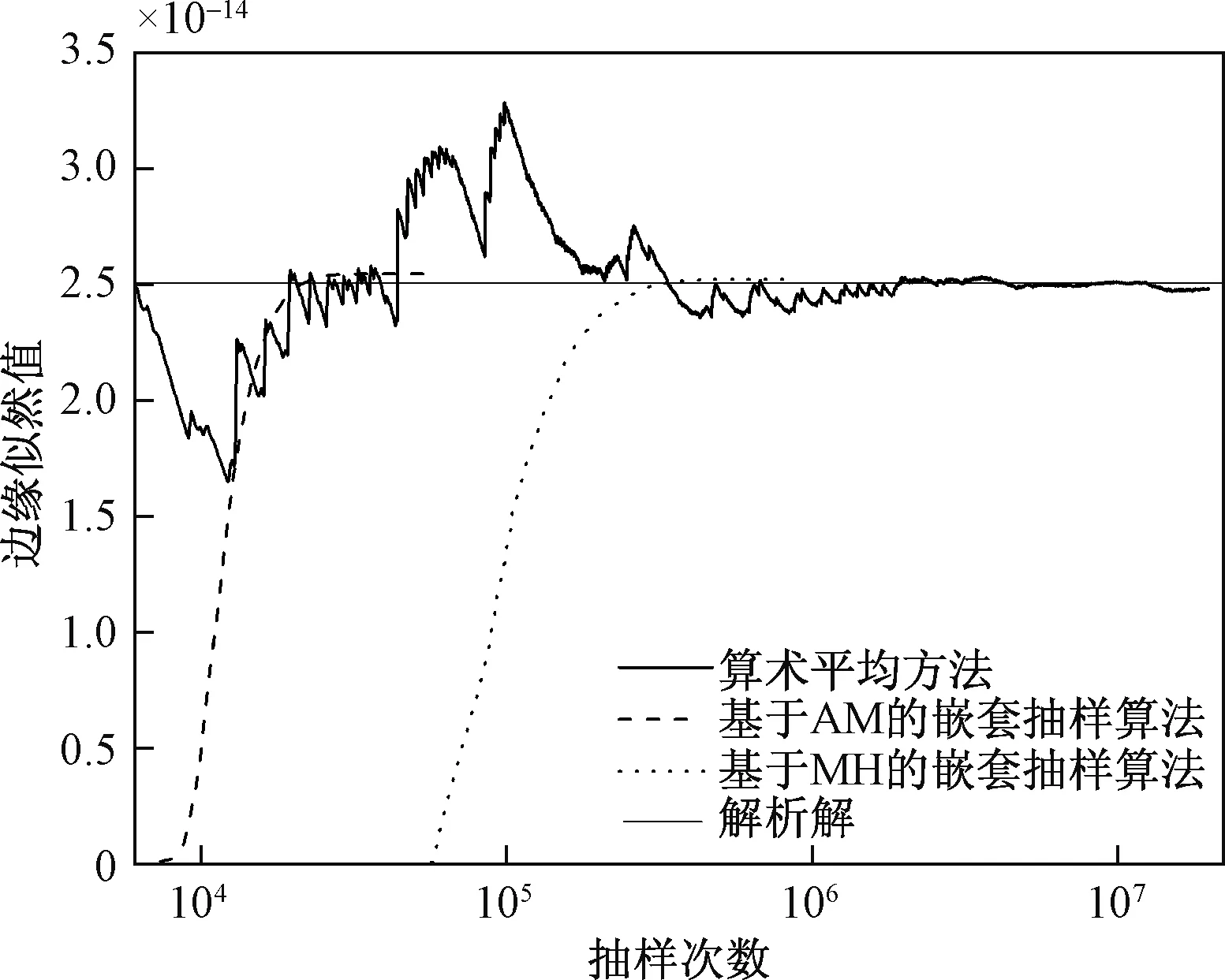


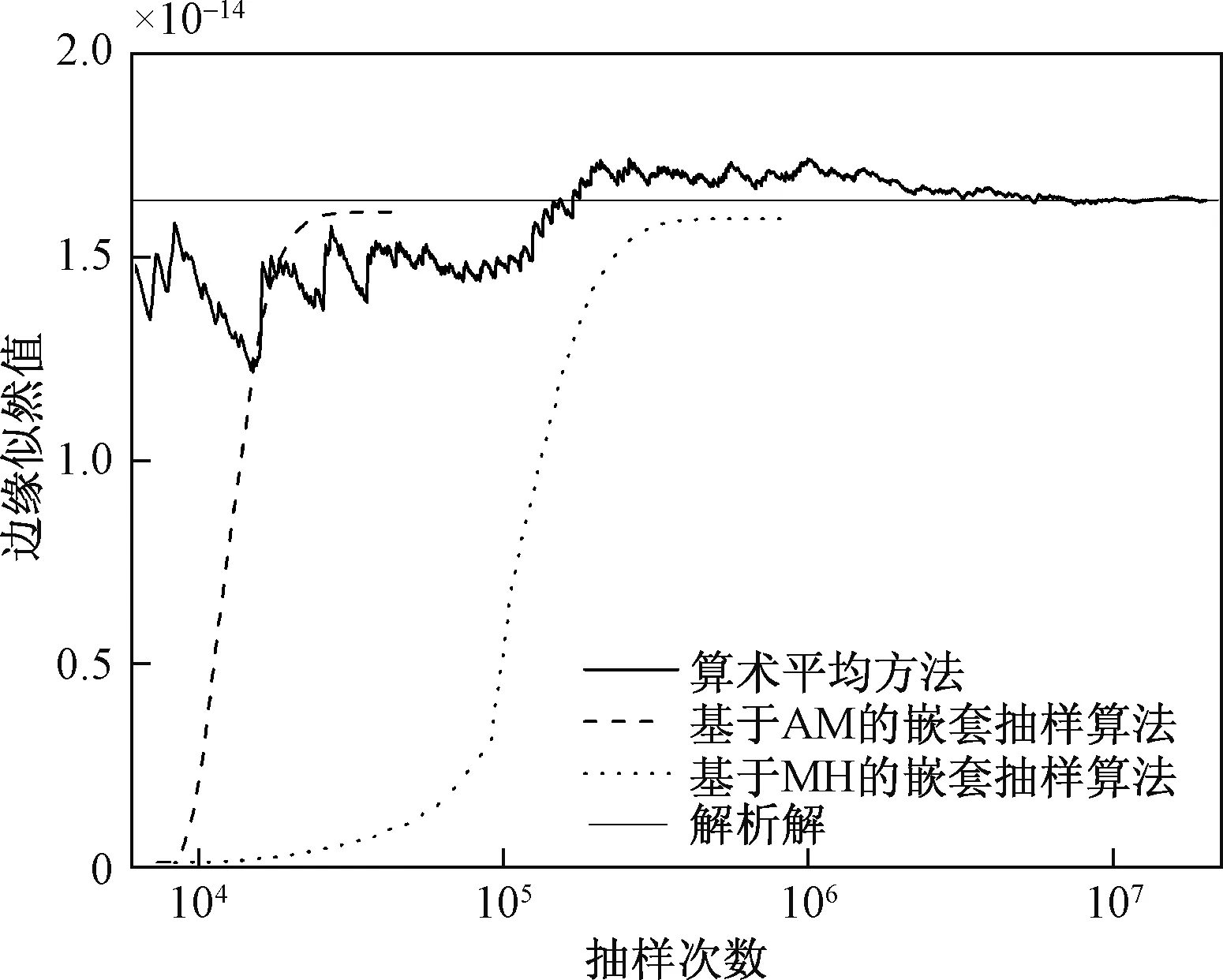

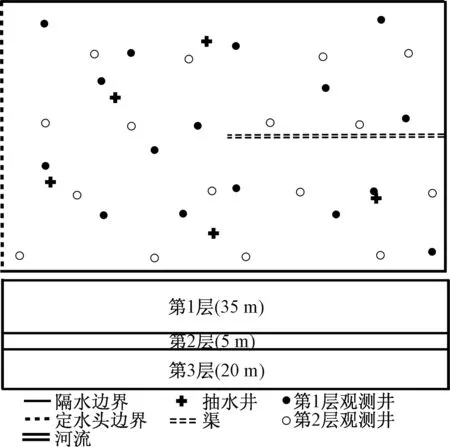
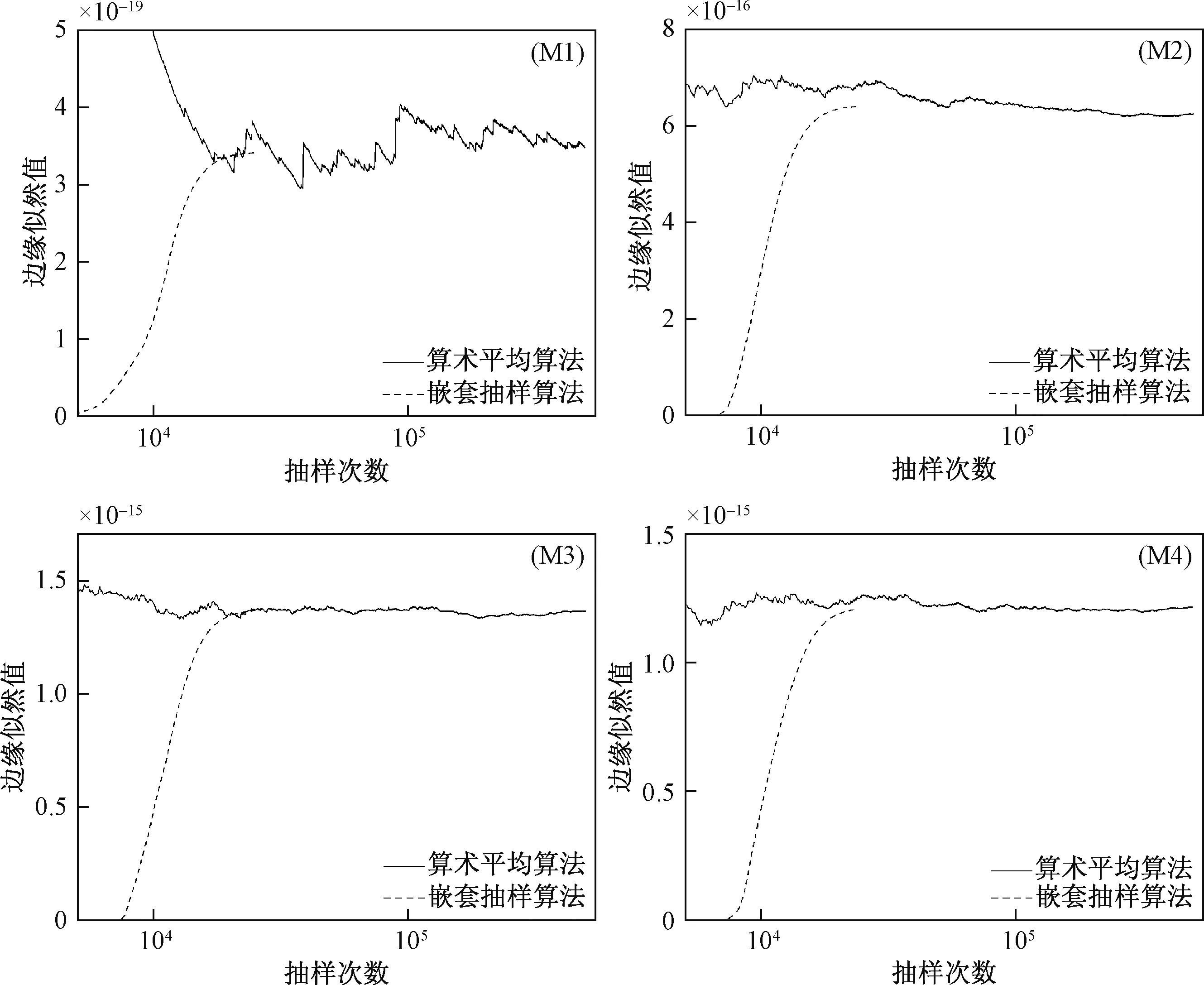



3 结论

