独立覆盖误差分析的子模型法

,,

(1.长江科学院 材料与结构研究所，武汉 430010;2.水利部水工程安全和病害防治工程技术研究中心，武汉 430010)

独立覆盖误差分析的子模型法

苏海东1,2,袁笑晨1,龚亚琦1,2

(1.长江科学院 材料与结构研究所，武汉 430010;2.水利部水工程安全和病害防治工程技术研究中心，武汉 430010)

2017,34(12):147-154

在应用独立覆盖流形法进行自适应分析的前期研究中，发现独立覆盖内部误差不易控制的问题,基于此，提出独立覆盖误差分析的子模型法。在单独的独立覆盖内进行覆盖函数的升阶操作，通过高、低阶之间的相对误差获得独立覆盖内部的逐点误差指标。详细介绍了子模型法的实施步骤，用重力坝算例验证了该方法能有效控制独立覆盖内部误差，不仅解决了目前存在的问题，还为将来实现逐点的误差控制打下基础。最后对独立覆盖流形法的收敛原理及误差控制方法进行了初步的理论分析和讨论。

数值流形方法；独立覆盖；误差分析；子模型法；自适应分析

1 研究背景

在计算机辅助工程分析(Computer Aided Engineering,CAE)中实现最少的人工操作以至于完全的自动计算，这是数值计算的发展方向。目前使用最为广泛的CAE方法是有限元法[1]，各种大型商用有限元软件都在逐步地减少人工操作，但有限元法一直存在的前处理网格剖分以及计算精度控制等问题还有待根本性的解决。其他新兴的数值计算方法，如广义有限元法[2]、无网格法[3]等，能够避免或部分解决有限元法的一些问题，但目前都还处在完善基础理论的阶段。笔者在前期提出的基于独立覆盖的数值流形方法(简称独立覆盖流形法)[4]，具有前处理方便、计算误差相对容易控制的优点，已采用矩形独立覆盖成功地进行了结构静力分析的自动化尝试[5]，以及CAD与CAE的融合研究[6]，展示了实现自动计算的潜力。

自适应分析是自动计算的基础，它运用反馈机理，根据上一次的计算结果来修改模型，逐步减小误差以达到所需的计算精度。自适应分析的核心是误差估计，或称为误差分析。笔者在文献[5]中针对独立覆盖流形法提出3种误差估计指标，通过多个算例验证，表明在多数情况下能够控制计算精度。但进一步研究发现，其中的独立覆盖高阶误差指标的作用不显著，从而在一些情况下造成独立覆盖内部误差没有被捕捉到。

本文提出独立覆盖误差分析的子模型法，在单独的独立覆盖内进行覆盖函数的升阶操作，通过高、低阶之间的相对误差获得新的误差指标，不仅解决目前存在的问题，而且为逐点的误差控制打下基础。

2 独立覆盖流形法及其误差估计问题

1991年，石根华博士发明了数值流形方法[7](以下简称流形法)，采用数学网格覆盖求解域。如图1所示。

图1 矩形独立覆盖系统

2012年，笔者在流形法中首次引入“独立覆盖”[8-9]，即单位分解函数φi=1、近似函数V就是给定级数Vi的覆盖区域。独立覆盖之间用窄条相连，其单位分解函数取为有限元线性形函数从而实现覆盖函数的线性过渡。首先研究了如图1(a)所示的矩形覆盖系统，每个矩形覆盖包含一个独立覆盖(图中的大矩形网格)及其周边的条形区域，条形是相邻覆盖之间的重叠区域。同时，还提出了覆盖加密方法[10]，比如将图1(a)所示的独立覆盖f和g分割成图1(b)所示的小覆盖。除了矩形独立覆盖外，2013年提出任意形状的独立覆盖[11]。

2015年笔者在文献[4]中将上述方法正式命名为“基于独立覆盖的数值流形方法”，并从协调性和完备性2个方面论述了方法的收敛性，同时指出：求解域的整体收敛是基于各覆盖自身收敛而建立的；随着覆盖函数的升阶，不仅物理场本身是收敛的，其导数也是收敛的；覆盖网格具有任意形状、任意连接和任意加密的特性。其中，任意连接是指独立覆盖之间的条形可以任意地错位布置，如图1(b)显示的大、小覆盖之间的连接方式。任意加密是指：不管采用何种加密方式，只要各覆盖均加密至适当大小，总可以做到在各覆盖内用适当阶次的完备级数逼近真实解。上述特性为前处理和误差估计提供了方便。

笔者根据独立覆盖的特点初步提出了3种后验误差指标(以结构静力分析为例)：条形区域的应力连续性指标η1，表示各覆盖的应力在条形重叠区域的连续性；边界应力指标η2，表示自由边界上的应力计算值与实际值的差异；独立覆盖内的高阶误差指标η3，表示在独立覆盖内应用高1阶的多项式对残差进行修正。各指标的具体表达式见文献[5]，均为用积分形式表述的平均误差。在此基础上，利用覆盖网格任意加密的特性，基于矩形独立覆盖进行了h-p型混合自适应研究，初步实现了与AutoCAD相融合[6]的二维结构线弹性静力分析的自动计算：人工只需在CAD中输入结构外形、材料参数和边界条件，其他所有的CAE分析工作完全交由计算机完成。

进一步研究发现，前2个指标非常有效，但η3即独立覆盖高阶误差指标的作用不明显，该指标基于能量模的平均误差，难以捕捉到独立覆盖内部的误差分布。下面看一个典型例子，见图2。

图2 含边界裂纹的平板及流形覆盖网格

如图2(a)所示的无限长条平板，两端受均布拉力P=0.3 kN/cm，平板宽w=0.4 m，含边界裂纹长a=0.05 m，计算I型裂纹的应力强度因子KI，理论值为1.45 kPa/m1/2[12]。

采用自动计算技术，误差限值取η1=5%，η2=0.001 MPa，η3=5%。覆盖网格加密成图2(b)的形式(模型底部全约束)，其中，含裂纹的中部区域在图2(c)中放大，在裂纹所在的网格号为63的独立覆盖中采用了反映裂尖附近位移的Williams解析级数作为覆盖函数。

考察图2(c)右端边界处网格号为11的独立覆盖，计算机自动设为2阶多项式，结果表明，预设的误差指标包括η3均满足。然而，如果人为地将2阶提高为4阶，那么在整体模型重新计算后，整理得到该网格在右端边界上的垂直向应力随y坐标的变化，见图3(a)，可以看出2阶和4阶多项式的应力分布有较大差别，有些部位2阶多项式相对于4阶多项式的误差超出了5%。

再看应力强度因子的计算。当计算机自动设置阶次时，随着63号网格内解析级数的项数增加，KI最多只能计算到1.40 kPa/m1/2左右。但如果人为地将11号网格的阶次从2阶提高为4阶，则KI可以算出1.45 kPa/m1/2的理论值。从裂纹所在水平线上的垂直向应力随x坐标的分布(如图3(b))可以看出，2阶情况在右端附近存在应力误差，而整条线上要保持力的平衡，从而影响到左端裂纹附近的应力分布，造成应力强度因子的计算误差。这表明，独立覆盖的内部误差控制是很重要的，如果控制不好，还有可能导致其他区域的计算精度受到影响。

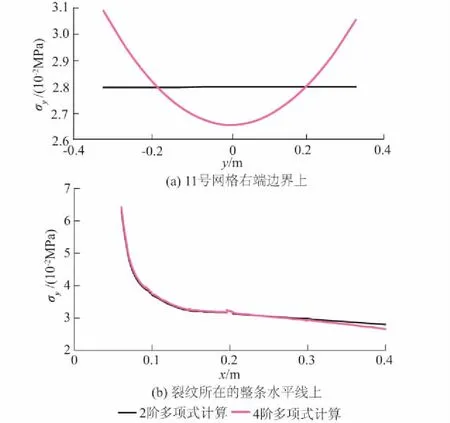
图3 11号网格右端边界和裂纹所在的整条水平线上的 垂直向应力分布

还从其他多个算例中发现：当某个独立覆盖的η3不满足预设误差限值时，其周边一般至少有一个条形的η1是不满足的；反之，当周边所有条形的η1均满足时，η3一般未出现不满足的情况。可见，η3与η1功能重叠，我们需要寻找能表征独立覆盖内部误差的其他指标。

3 独立覆盖子模型

从第2节的算例可以看出，覆盖函数升阶可以有效提高精度。在以往的P型有限元中，高阶计算对低阶计算的改进是很重要的误差指标。一般认为，在一定的网格密度下，当低阶和高阶的计算结果相近时，可以初步判定(但不能完全确定)达成了收敛。通常情况下，低阶和高阶的整体模型都要计算，才能进行对比。

然而到目前为止，我们仍采用基于当前计算结果的后验误差估计，而不是前后2次计算的对比。这样做的优点是可以减少计算量，如果只用当前的计算结果就能判定，就没必要再计算升阶后的整体模型；而不足之处是难以用到“高低阶对比”这个有效指标。因此，本文寻求仅需小规模高阶计算的替代方法，这就是子模型法。

传统的子模型法是一种有限元分析技术，指的是从原模型中切出用户关心的区域，进行细化网格的分析，从而得到结构局部区域更加精确的解而不增加计算规模。子模型法又称为切割边界位移法，“切割边界”就是子模型从大模型中分割开的边界，将大模型计算的位移值施加在切割边界上作为子模型的边界条件。

本文提出独立覆盖的子模型法，将某个独立覆盖及其四周的条形作为一个子模型的覆盖网格，条形周边作为子模型的切割边界。如图4(a)所示的大模型的覆盖网格，从中切取独立覆盖b及周边条形，形成图4(b)的子模型。与传统有限元的子模型稍有不同的是：切割边界上的已知边界条件是由大模型计算得到的各边界结点(如图中的点2，5，8，11，14-17)上的多项式系数，而不是有限元法的结点位移；子模型的覆盖网格区域与流形元的积分区域(图4(b)粗线内的区域)也可能不一致。子模型法相当于建立一个隔离体，上述切割边界上的已知边界条件反映的是相邻覆盖网格中流形元对子模型中流形元的作用;除此之外，子模型上如果存在的约束条件、荷载(包括自由边界上的应力边界条件)都需要施加，才能构成一个完整的平衡力系。

图4 矩形覆盖的子模型

在子模型上建立方程组的过程与整体模型一致，都需要对各个覆盖网格(包括独立覆盖和条形)内的流形元生成刚度矩阵和荷载向量。以图4(b)中结点2,3,9,8构成的条形网格为例，经过对该网格内的流形元进行刚度积分并计算荷载后，形成单元方程如式(1)所示。

(1)

式中：A2，A8分别为已知边界条件的结点2和结点8上的多项式系数组成的子向量；A3，A9分别为待求结点3和结点9上的多项式系数组成的子向量；Kij，Fj(i,j=2,3,9,8)分别为与之相应的刚度矩阵和荷载向量的分块子矩阵和子向量。

只保留含有待求未知量的方程，将左端的已知系数和相应刚度系数的乘积移至方程右端，得到单元方程为

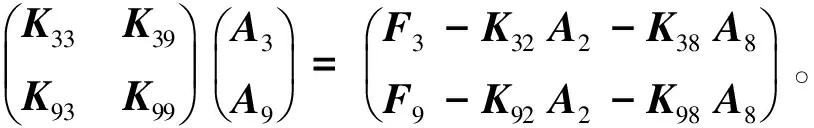
(2)

然后组集所有单元形成整体刚度矩阵和向量，在组集过程中，考虑对独立覆盖采用文献[8]提出的强制约束方法，即令A4=A9=A10=A3，将“从结点”4,9,10上的刚度子矩阵和子向量叠加到“主结点”3的相应位置，最终形成线性无关的代数方程组，其未知量仅为A3，采用高斯消元法求解，计算量很小。

当子模型上有约束信息时，若按通常流形法采用硬弹簧(即罚函数法)的方式施加约束，则弹簧系数(即罚数)的取值对计算结果有一定的影响。笔者在文献[13]中提出，通过改变多项式的局部化表达式使独立覆盖函数自动满足边界条件，不仅能得到稳定的计算结果，而且能使未知量进一步减少。

4 考虑子模型法的自动计算及独立覆盖内部误差指标

引入子模型法后，自动计算的具体步骤初步调整如下：

(1) 按文献[5]的过程，基于η1和η2两个误差指标进行h-p型混合自适应分析，直至整个求解域满足预设精度要求(应力奇异区除外)，即各覆盖的应力值在条形重叠区域内基本连续。将此时的计算模型作为子模型分析前的原模型。此做法的依据在于：子模型的边界条件来自大模型的计算结果，只有在这些边界条件达到一定精度后，子模型法才能得到相对准确的内部计算结果;否则，如果作用在子模型上的边界条件和实际相差较大，那么子模型的结果就没有参考价值。

(2) 对各个独立覆盖形成子模型的数据文件，包括子模型上的流形元几何、约束、荷载、材料参数等信息，以及已知边界条件。由于子模型与大模型的相应部分完全相同，因此直接从大模型中提取有关数据，包括从计算结果中提取切割边界上的多项式系数。

(3) 分析子模型。将子模型中的独立覆盖函数升阶，按上节所述过程进行计算，再与原阶次的应力结果对比，作为新的独立覆盖内部误差指标η3，具体表达式在本节后段讨论。

(4) 如果各独立覆盖的子模型均满足预设精度，则计算结束；否则，根据子模型的计算结果，提高大模型中相应独立覆盖的阶次，或进行覆盖加密，重新计算改进后的大模型，然后回到步骤(2)，对相关的独立覆盖再次验算η3。

这里仍以图2所示的算例为例。对11号网格的独立覆盖建立子模型，由原来的2阶分别升到3阶至6阶，计算得到右端边界上的垂直向应力分布如图5所示。

图5 11号网格右端边界上的垂直向应力分布 (子模型法)

结果分析如下：

(1) 作为验算，首先计算子模型的2阶，其结果与大模型非常接近，表明了方法和程序的正确性。

(2) 3阶结果与2阶相差不大；但升至4阶后计算结果有相对较大的变化，最大差值为0.13×10-2MPa，相对增幅为4.6%；而4，5，6阶变化较小，最大差值<0.03×10-2MPa，相对增幅1%左右，表明在子模型中升至4阶已能得到基本稳定的应力结果。

(3) 子模型的4阶应力与图3中的整体模型4阶应力分布接近，数值稍有差异，最大差值约0.1×10-2MPa，反映了整体模型内部的相互影响，因此有必要回到大模型再进行一次整体计算。

子模型的高阶结果与大模型整体计算的高阶结果相近的事实，给出了一个重要启示：可以将高阶子模型的应力计算结果作为相对正确解σ*，而原阶次计算的σ与σ*的差别作为内部误差指标η3，即

(3)

应用式(3)对各应力分量进行操作，并在子模型中逐点计算，从而得到逐点的应力误差。考虑到式(3)是函数表达，可以借助求解函数极值的程序，找到独立覆盖区域内的相对误差或绝对误差的最大值，与预设精度进行比较。

子模型升至足够高的阶次后，若应力精度仍不达标，则提示当前覆盖需要加密。在一些情况下，误差较大的区域可能就是需要加密的部位，如图5所示的独立覆盖的上下两端。对于包含应力奇异区(如凹体的尖角)的独立覆盖，应力不稳定是无法避免的，一般需要多次的覆盖加密，使应力不稳定的区域局限在很小的范围内。

5 重力坝算例

如图6(a)所示的重力坝，坝高100 m，坝底、坝顶长分别为60 m和20 m，下游面折角处距坝顶20 m，坐标原点位于坝踵处。重力坝底部施加全约束，上游面承受库水压力荷载，库水深80 m。坝体弹性模量为30 GPa，泊松比为0.167。考虑到本算例没有解析的解答，因此采用划分了足够细密网格的有限元结果作为参考解，如图6(b)所示，划分15 840个4结点等参元，结点数为16 245。

图6 重力坝示意图和有限元网格

图7 原模型的覆盖 函数阶次

误差限值取η1=5%，η2=0.001 MPa。设定5×5的初始覆盖网格，基于这2个精度指标进行自适应分析。当覆盖网格加密成图7所示的形式时，除坝踵、下游面折角等应力奇异区外，其他绝大部分区域的误差均小于给定的误差限，故可将图7所示的计算模型作为原模型。对所有独立覆盖逐个建立子模型进行收敛判断，与设定的相对误差限η3=5%比较，决定是否升阶或加密。以下分别以图7中的1号和110号覆盖网格为例，说明子模型的分析结果。

(1) 计算1号网格的独立覆盖3阶原模型和4阶子模型在独立覆盖区域内的应力及误差分布，找到点(35.63，2.952)处的σx分别为-10.506 ×10-2MPa和-9.562 ×10-2MPa，是相对误差最大之处，为9.87%。如图8所示在区域内x=30 m线上的σx分布，可以看出原模型与子模型的应力变化趋势是一致的，只是数值稍有差异。

图8 1号网格的σx沿x=30 m的分布

(2) 110号网格在原模型中的位移函数为3阶，对其建立4阶子模型，σy沿上游面的分布如图9所示。由图9可知,原模型与子模型的应力解稍有差异但变化趋势一致，特别是在点(0,70.62 m)处，σy分别为-0.106×10-2MPa和0.214×10-2MPa，相对误差为149%。同时整理了上游面几个特征高程处的σx应力见表1，与库水压力的理论值对比，可以看出，3阶多项式相对于4阶的误差均已<1%，但高阶子模型的结果更趋近于理论值，表明用其作为参考值来反映独立覆盖的内部误差是合理的。

图9 110号网格的σy沿上游面的分布

Table 1 Values of σx at different elevations alongthe upstream face in mesh No.110 10-2 MPa

图10 改进模型的 覆盖函数阶次

所有独立覆盖进行了子模型分析后，得到图10所示的局部升阶后的改进模型，对其进行整体计算。然后将改进模型作为原模型再次进行子模型分析，结果如下：

(1) 1号网格中，x=30 m线上的σx应力分布及与有限元结果对比见图11，可以看出改进模型的4阶与子模型的5阶应力曲线几乎完全重合。改进模型的应力曲线与有限元解曲线基本重合，只在中段有很小差异。以有限元解为参考解，改进模型的相对误差最大值为2.31%，相比其与3阶原模型的最大相对误差(8.89%)有了较大改善。1号网格内，改进模型与5阶子模型的σx相对误差最大值为2.18%，已小于设定的η3指标，无需再升阶。

图11 1号网格的σx在x=30 m线上的应力对比

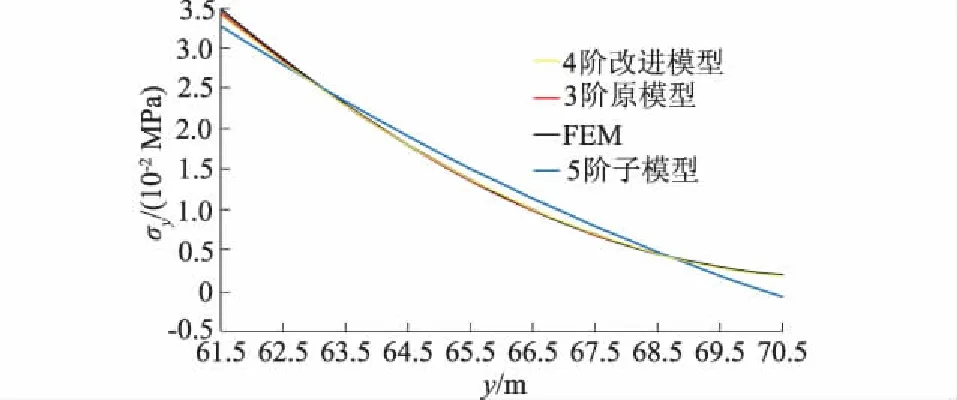
图12 110号网格的σy沿上游面的分布对比

(2) 110号网格在改进模型及5阶子模型中的σy沿上游面的分布见图12，并与3阶原模型以及有限元解比较。可以看出改进模型的σy应力曲线几乎与有限元解重合。以有限元解为参考解，相对误差最大值由3阶原模型的139%降至改进模型的10%，相应的绝对误差由0.27×10-2MPa降至0.02×10-2MPa，说明改进模型的独立覆盖内部精度有了明显提高。110号网格内，改进模型与5阶子模型的相对误差最大值为10%，虽然仍大于设定的η3指标，但考虑到该部位本身应力值很小(0.002 MPa左右)，因此无需再升阶。在坝顶区域的多个独立覆盖中，也存在相对误差大但应力绝对值很小的类似情况。

个别独立覆盖，如图7中45号网格，经过1次改进后，应力相对误差仍较大，说明仅仅采用升阶操作(已升至5阶)还不能达到计算精度，提示需要加密覆盖，然后再通过反复的子模型分析使之收敛。

6 讨 论

(2) 应用微分方程的积分解法进行求解，比如加权残值法中的伽辽金法(在结构分析中即最小势能原理)，当覆盖函数为一定阶次的多项式级数时，并不直接等同于真实场函数的泰勒展开，而是一种积分意义下的平均收敛，反映的是区域内误差的整体度量(即平均误差)随着阶次提高而逐渐减小。具体到各点，虽然不一定是随阶次单调地逼近，但各点误差在整体趋势上一定是减少的，覆盖函数逐步趋向于(1)中所述的分区级数解。因此，用高阶相对于低阶的改进作为误差指标具有渐近精确性。

(3) 独立覆盖流形法采用以独立覆盖为主的分析方式，独立覆盖占据求解域的绝大部分区域，是产生整体平均误差的主体。因此，我们着重于各独立覆盖的内部误差估计。在各覆盖之间的应力基本连续的条件下，子模型法可以用很小的计算量得到高、低阶相对误差指标，并能计算出逐点误差。通常的有限元法、无网格法等采用ZZ法通过应力重构得到相对准确的应力值作为对比[14-15]，但准确应力场的获得往往伴随着较大计算量。

(4) 在独立覆盖内，子模型法可以反映一定边界条件下对微分方程真实解的逼近。但此真实解并不等同于整体求解的真实解，因为代表相邻覆盖对其作用的边界条件不一定准确，而只有在其他覆盖均达成逼近时才是准确的，此时，整体近似函数将成为(1)中所述的分区级数解。这就是经过子模型改进后还需整体计算、甚至不断反复的原因。事实上，ZZ法反映的也只是局部精度，对于结构静力分析这类椭圆型偏微分方程，文献[16]用算例说明了来自远场的所谓“pollution error”的影响，与本文的应力强度因子算例揭示的现象一致。

(5) 以上分析仅仅从截断误差或离散误差考虑，没有论及舍入误差或计算误差。理论上，提高阶次一定会带来精度的改善，但过高的阶次会使计算误差难以控制。在实际操作中建议采用适当的级数阶次，而减小覆盖尺寸是另一选择，下一步的子模型法可以尝试在子模型中加密覆盖，逐点误差可以指示加密区域，有利于自适应路径的优化。另外，通常所取的条形厚度(目前建议条形面积占覆盖面积1%～10%)远不至于影响到方程组的求解精度。如(1)中所述，条形网格的收敛含义不同于常规的有限元网格，关于条形厚度及形状影响计算精度的疑虑是不必要的。

(6) 在逐点误差计算的基础上，将来通过对误差指标和自适应路径的合理安排，有望达成逐点的误差控制，使偏微分方程基于积分解法的数值计算实现从“平均收敛”到“一致收敛”，即求解域内各点误差均小于某一限值。但在实际情况下，也要考虑人们对误差的接受程度，比如在应力很小的部位，稍有改变就可能带来较大的相对误差，而实际上没有必要再去改进。这也关系到自动计算的效率问题，反复的自适应分析会带来较大的计算量。笔者正在尝试一系列手段来提高效率，比如在裂尖附近等特殊区域利用解的先验知识预先布置好局部覆盖，以及利用前次计算结果加快当前计算等，这些研究将另文介绍。

7 结 语

本文首先通过一个计算I型裂纹应力强度因子的算例说明控制独立覆盖内部误差的重要性，然后提出独立覆盖的子模型法，将高、低阶的应力对比作为新的独立覆盖内部误差指标，并用重力坝算例演示了自动计算中的子模型法，验证了本文方法对独立覆盖内部误差的有效控制,为将来实现逐点误差控制打下基础。最后，关于独立覆盖流形法的收敛原理及误差控制方法，给出一些定性的理论分析和讨论。

致谢：感谢石根华博士的指导！

[1] 王勖成．有限单元法[M]．北京：清华大学出版社，2003.

[2] STROUBOULIS T, COPPS K, BABUSKA I. The Generalized Finite Element Method[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(32):4081-4192.

[3]BELYTSCHKO T, KRONGAUZ Y, ORGAN D,etal. Meshless Methods: An Overview and Recent Developments[J]. Computer Methods in Applied Mechanics and Engineering , 1996, 139(1/2/3/4): 3-47

[4] 苏海东，颉志强，龚亚琦, 等．基于独立覆盖的流形法收敛性及覆盖网格特性[J]. 长江科学院院报，2016，32(2)：131-136.

[5] 苏海东，龚亚琦，颉志强, 等. 基于矩形独立覆盖初步实现结构静力分析的自动计算[J]. 长江科学院院报，2016，33(2)：144-150.

[6] 苏海东，陈积瞻，颉志强, 等. 基于独立覆盖流形法的CAD与CAE融合研究[J]. 长江科学院院报，2017,34(12):133-139.

[7] SHI G H.Manifold Method of Material Analysis[C]∥U.S. Army Research Office. Transactions of the Ninth Army Conference on Applied Mathematics and Computing. Minneapolis, Minnesota, U. S. A, June 18-21,1991:51-76.

[8] 祁勇峰, 苏海东, 崔建华．部分重叠覆盖的数值流形方法初步研究[J].长江科学院院报, 2013,30(1):65-70.

[9] SU Hai-dong, QI Yong-feng, GONG Ya-qi,etal. Preliminary Research of Numerical Manifold Method Based on Partly Overlapping Rectangular Covers[C]∥DDA Commission of International Society for Rock Mechanics. Proceedings of the 11th International Conference on Analysis of Discontinuous Deformation (ICADD11). Fukuoka, Japan, August 27-29, 2013, London :Taylor & Francis Group, 2013: 341-347.

[10] 苏海东,祁勇峰. 部分重叠覆盖流形法的覆盖加密方法[J]. 长江科学院院报, 2013,30(7):95-100.

[11] 苏海东, 祁勇峰, 龚亚琦, 等 任意形状覆盖的数值流形方法初步研究[J]. 长江科学院院报, 2013, 30(12): 91-96.

[12] 中国航空研究院．应力强度因子手册[M]. 北京：科学出版社，1993.

[13] 苏海东，颉志强．独立覆盖流形法的本质边界条件施加方法[J]. 长江科学院院报，2017,34(12):140-146.

[14] ZIENKIEWICZ O C, ZHU J Z. A Simple Error Estimator and Adaptive Procedure for Practical Engineering Analysis[J]. International Journal of Numerical Methods in Engineering,1987, 24(2): 337-357.

[15] CHUNG H J, BELYTSCHKO T. An Error Estimate in the EFG Method[J]. Computational Mechanics，1998，21(2)：91-100.

[16] BABUSKA I,STROUBOULIS T,GANGARAJ S K,etal. Practical Aspects of A-posteriori Estimation for Reliable Finite Element Analysis[J]. Computer & Structures, 1998, 66(5):627-664.

Submodel Method for Error Analysis in Numerical Manifold MethodBased on Independent Covers

SU Hai-dong1,2, YUAN Xiao-chen1, GONG Ya-qi1,2

(1.Material and Engineering Structure Department, Yangtze River Scientific Research Institute, Wuhan 430010, China; 2.Research Center on Water Engineering Safety and Disaster Prevention of Ministry of Water Resources, Wuhan 430010, China)

In previous research of adaptive analysis using Numerical Manifold Method based on independent covers, the internal error in an independent cover cannot be effectively controlled. In view of this, a submodel method for error analysis of independent covers is presented, in which, by means of increasing the cover function order in an individual independent cover, a new error estimator for point-by-point error is obtained by calculating the differences of the results between high-order and low-order cover functions. The procedures of the submodel method are introduced in detail, and a case study of a gravity dam shows that the method could effectively control the internal error of independent covers, laying foundation for point-by-point error control in the future. Finally some preliminary theoretical analysis and discussions are given for the convergence principle and the error-control method of Numerical Manifold Method based on independent covers.

Numerical Manifold Method(NMM)；independent covers；error analysis； submodel method；adaptive analysis

2017-02-13；

2017-03-17

国家自然科学基金项目(51409012)；中央级公益性科研院所基本科研业务费项目(CKSF2016266/CL)

苏海东(1968-)，男，湖北武汉人，教授级高级工程师，博士，主要从事水工结构数值分析工作和计算方法研究，(电话)027-82927167(电子信箱)suhd@mail.crsri.cn。

10.11988/ckyyb.20170128

TB115；TV311

A

1001-5485(2017)12-0147-08

(编辑：黄 玲)