具外部位势分数阶Choquard方程的基态解

刘瑞娜, 章国庆, 刘三阳

(1.上海理工大学理学院,上海 200093;2.西安电子科技大学数学与统计学院, 陕西 西安 710071)

具外部位势分数阶Choquard方程的基态解

刘瑞娜1, 章国庆1, 刘三阳2

(1.上海理工大学理学院,上海 200093;2.西安电子科技大学数学与统计学院, 陕西 西安 710071)

研究具外部位势非自治分数阶Choquard方程:

基态解的存在性.利用Nehari流形技巧、集中紧性原理和山路引理得到了基态解的存在性.

分数阶Choquard方程;外部位势;基态解

1 引言和主要定理

本文讨论如下具外部位势的非自治分数阶Choquard方程:

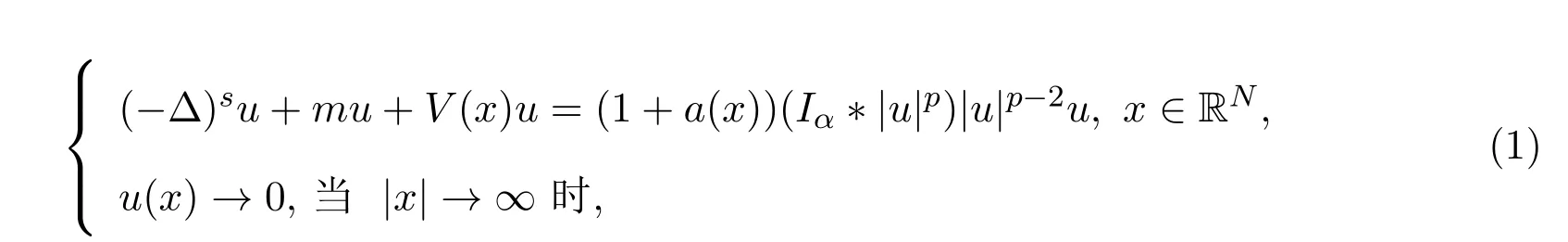
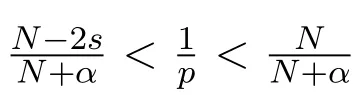
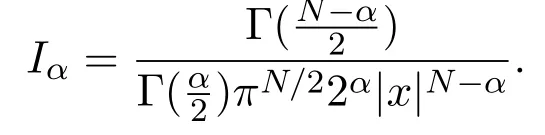
函数a(x)满足:A)a=a(x)∈L∞(RN),a(x)≥0,在RN上的正测度集上a(x)＞0.

外部位势函数V(x)满足:

H1)V(x):RN→R是连续有界函数,且V(x)≥−V0,其中:V0∈(0,1);

H2)V∞=liminf|x|→∞V(x)＞−1.

近年来,许多学者研究了上述类型方程并得到其解的存在性文献[1-2].文献[3]考虑了如下在RN的外部区域Ω内的方程:

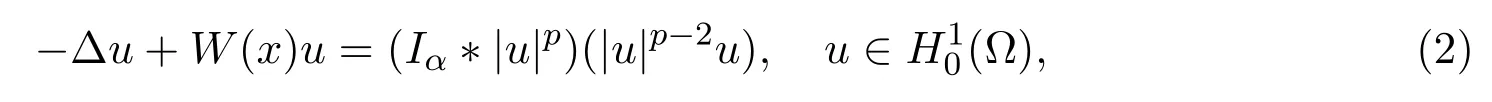
并得到了正解和变号解的存在性;文献[4]讨论了如下方程:

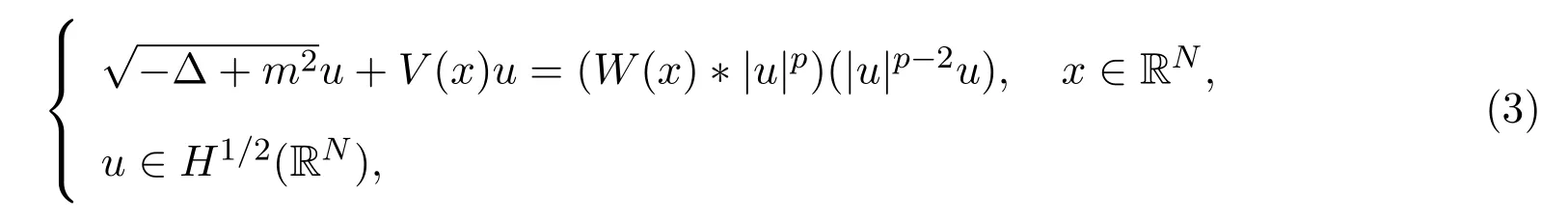
并证明了基态解的存在性;陈红艳和刘春根文献[5]研究了如下方程:

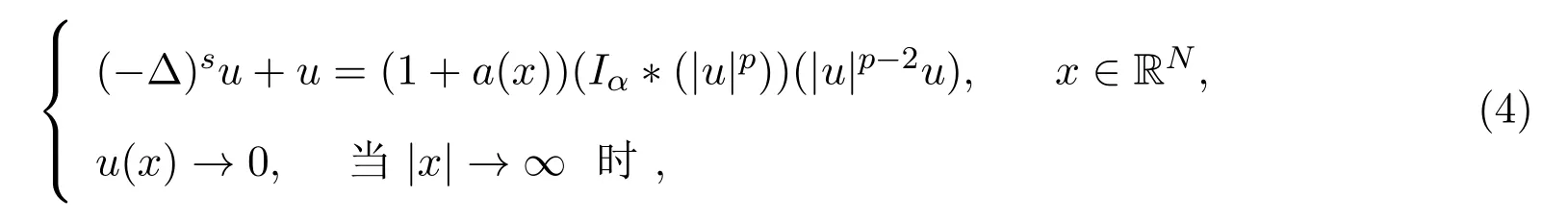
且利用Nehari流形技巧证明了基态解的存在性.

受文献[4-5]的启发,本文研究具外部位势非自治分数阶Choquard方程(1)基态解的存在性.为讨论问题(1),我们将利用文献[6]的技巧.即:对于一些定义在上半空间带有局部微分算子的椭圆边值问题,可将非局部的微分算子表示为一类Dirichlet-Nemann映射.

本文主要的定理为:

在第二节,我们给出一些预备知识.在第三节中,考虑问题(1)极限问题.在第四节中,证明了与方程(1)相关的能量泛函满足Palais-Smale条件(紧性条件).在第五节中,给出了主要定理的证明.

2 预备知识

现定义分数阶Sobolev空间Hs(RN)为:

相应范数为:

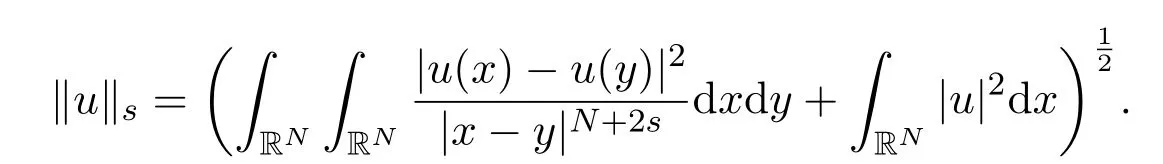
另外,据

这里F表示傅里叶变换.因此,对所有u∈Hs(RN),有

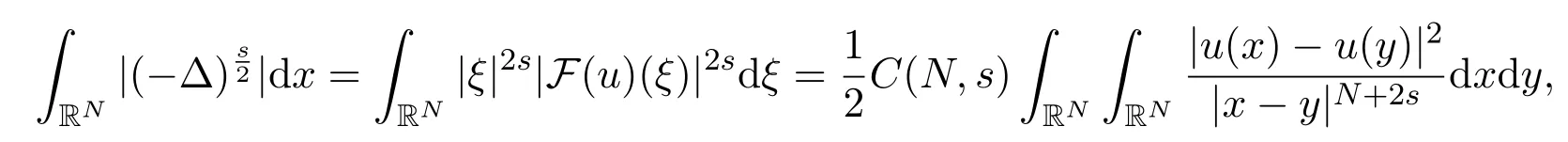
其中

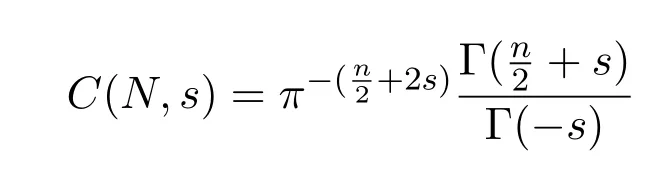
是一个常数文献[7],且当,嵌入映射是连续的,其中

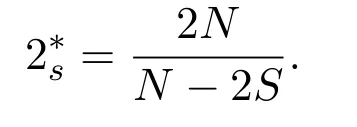
下的完备化空间.另外,

是连续的.接下来,我们定义

相应范数为:

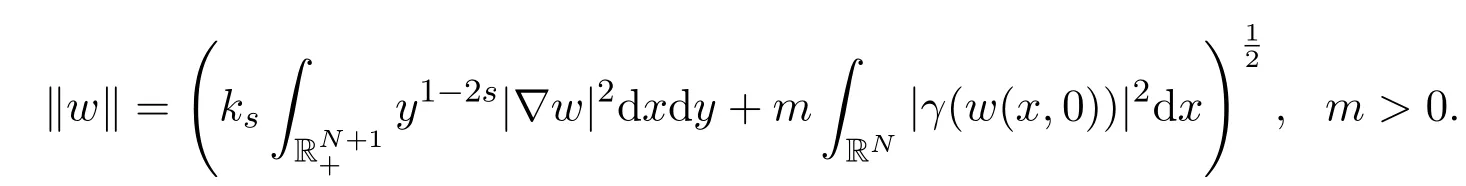
另外,

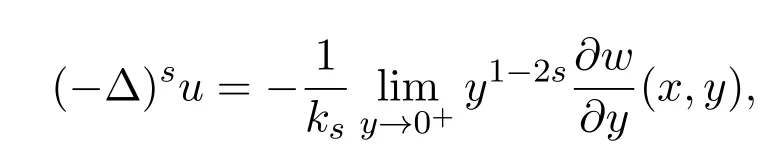
其中

令|·|q表示在中的范数,用|·|q(Ω)表示在Lq(Ω)中的范数,其中开区域.对于 Sobolev 空间,由迹函数理论知,对每个函数都存在迹函数γ(w)∈Hs(RN).

考虑下列方程:

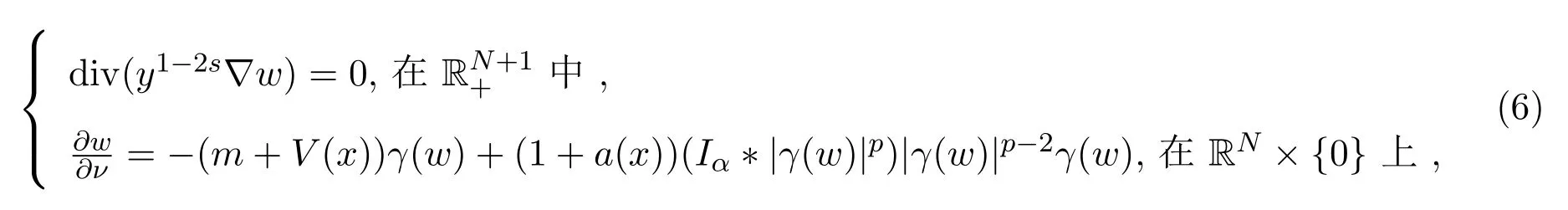
其中

则方程(6)相应的泛函J:E→R为:

首先,由V(x)有界及可得

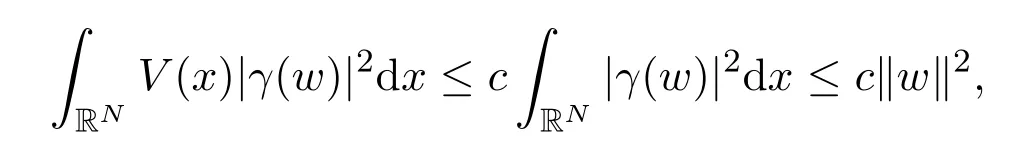
其中c是大于0的常数.另外,由Hardy-Littlewood-Sobolev不等式,可得

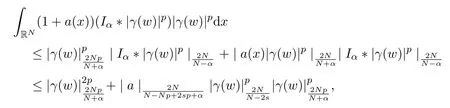
因此,泛函J(w)是有意义的.

经过计算,泛函J(w)∈C1(E,R)且有

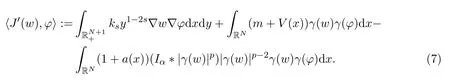
于是,根据文献[6]的结果可得,若w∈Xs(RN+1+)是问题(6)的解,那么

为方程(1)的解.

引理 2.1泛函J具有山路引理的几何结构,即

(i)J(0)=0,且存在ρ＞0,α′＞0对所有‖w‖=ρ,使得J(w)≥ α′＞0;

(ii)当λ→+∞时,存在w∈E{0},有J(λw)→−∞.

证明据

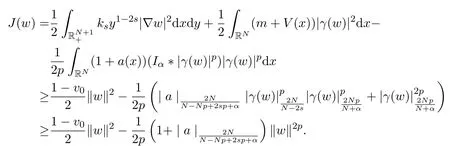
因此,可以找到c1＞0使得

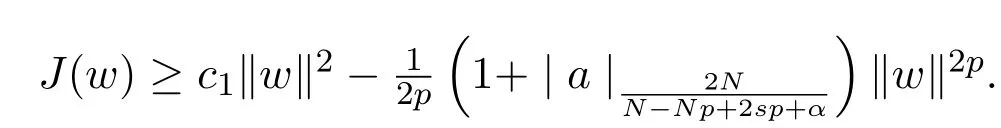
立即推出这存在ρ＞0,α′＞0使得对所有‖w‖=ρ,有J(w)≥α′＞0.另外,对存在w∈E,,易证,当λ→∞时,有J(λw)→−∞.因此,引理 2.1得证.

3 极限问题

当V(x)=V∞时,方程(6)的极限问题就变为

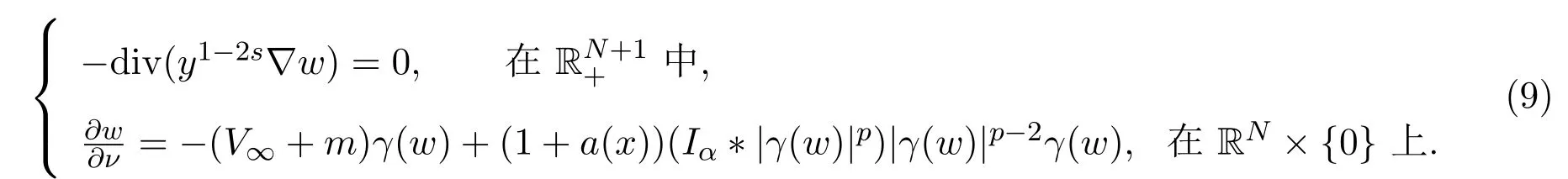
其中

考虑泛函JV∞(w):E→R且定义

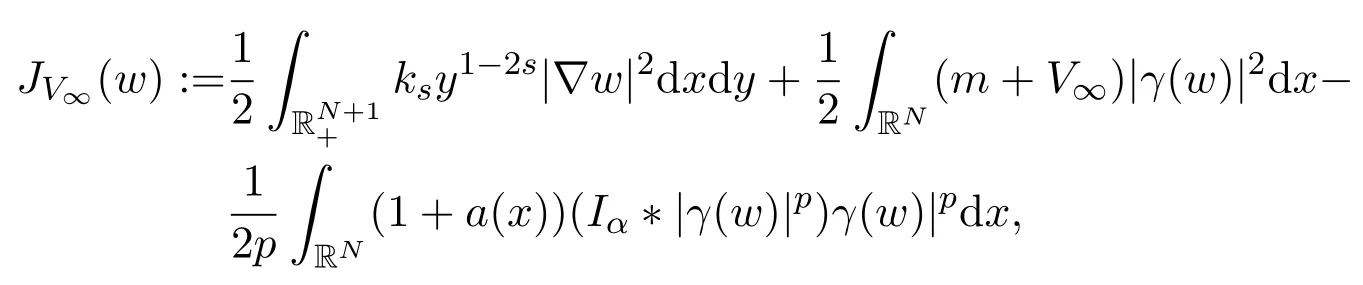
其中m＞0.接下来,定义与泛函JV∞(w)相关的Nehari流形NV∞,即

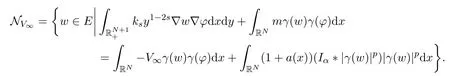
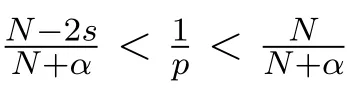
据文献[8]中定理4.3可得,泛函JV∞(w)具有山路型临界点wV∞∈E,即

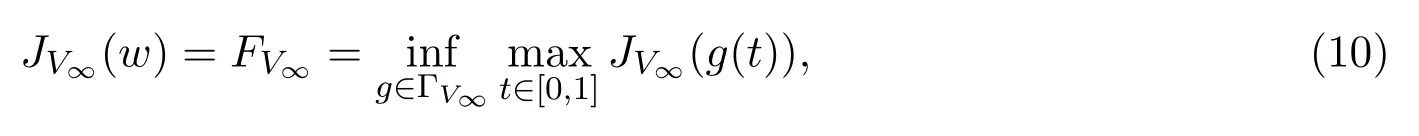
其中

引理3.2公式

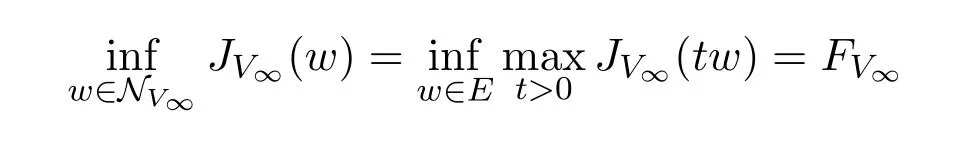
的证明.

证明对于任意w∈E,可得

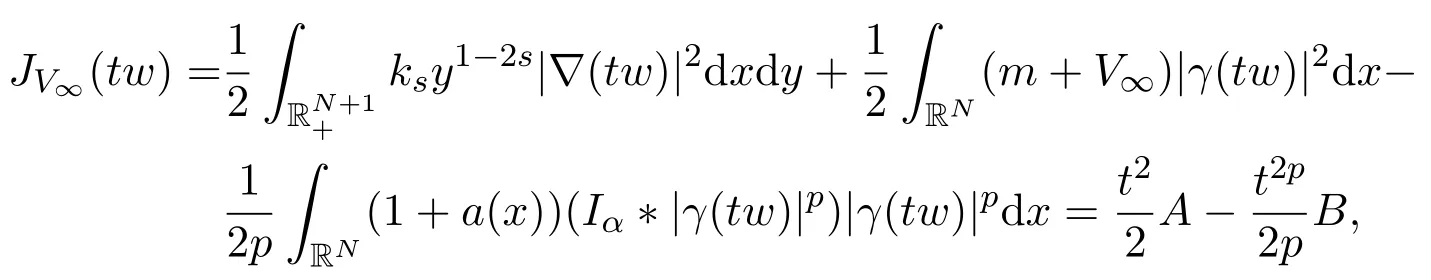
其中

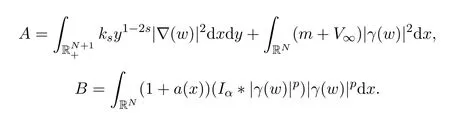
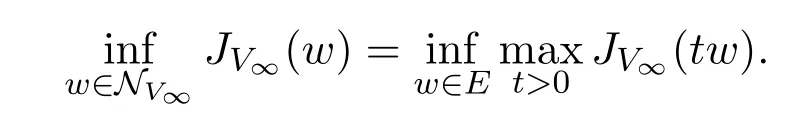
Nehari流形NV∞将E分成两部分,且包含0的部分是开的.另外,当 0＜t≤t(w)时,

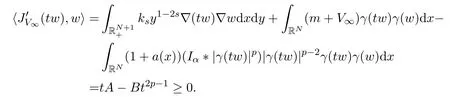
因此,在包含0的区域上JV∞是非负的.则道路γ:[0,1]→E,其中

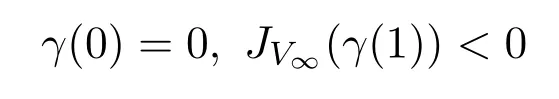
必须经过Nehari流形NV∞,因此,

综上可得,引理3.2得证.

4 Palais-Smale条件

引理 4.1设{wn}n是中的一个序列,使得在中wn⇀0,

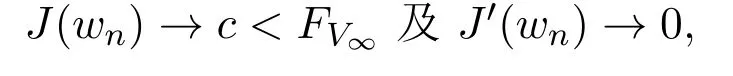
则{wn}n存在子列在中强收敛于0.

证明首先,定义J(w)的等价泛函为:

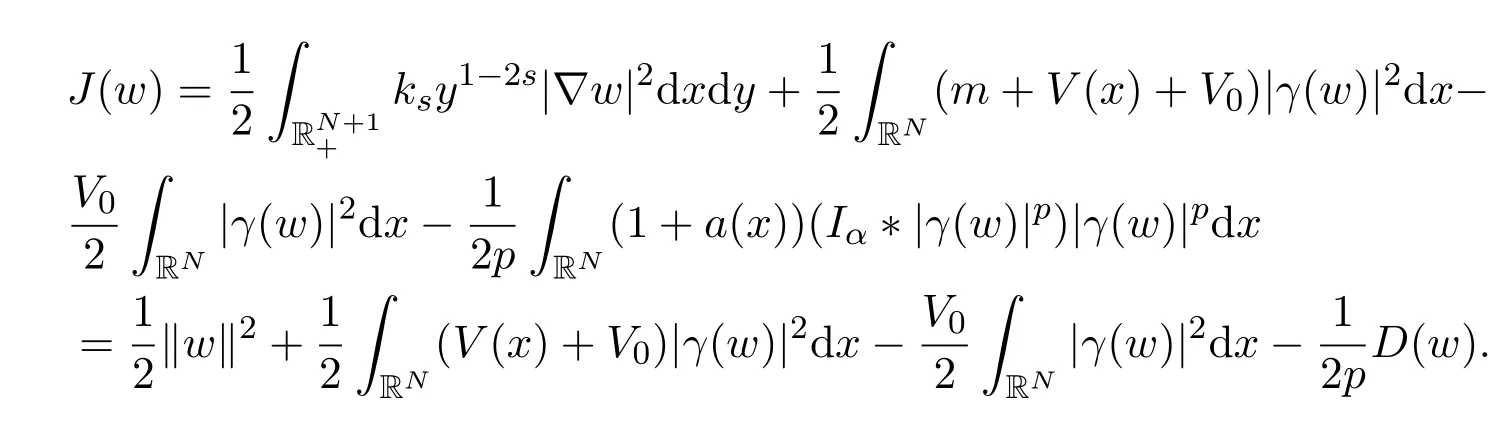
则据已知可得,

则存在常数C1和C2,有

又由于V(x)+V0≥0,以及

因此,{wn}n为中的一个有界序列,且可得

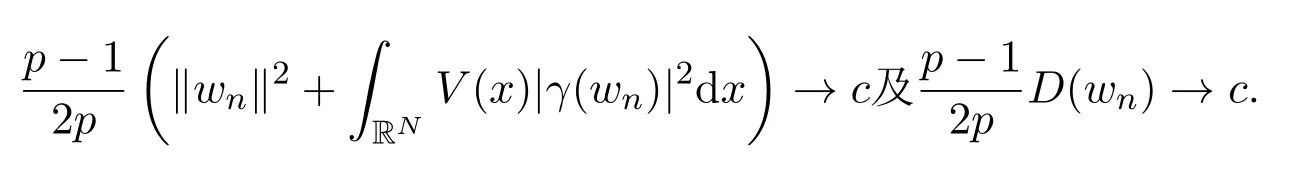
因此,c≥0.

若c=0,则

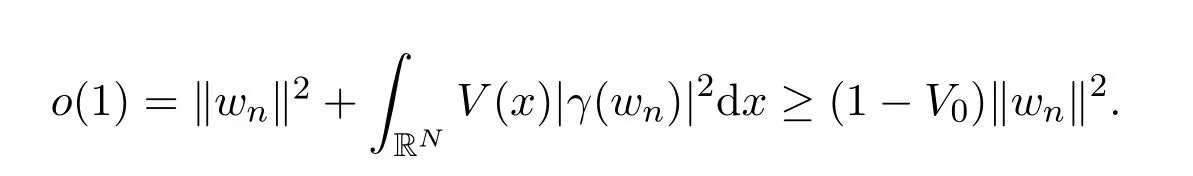
由于V0∈(0,1),故在中wn→0,即wn强收敛于 0.

若c＞0,假设当V∞＜V(x)时满足c＜FV∞,则据H2) 可得V(x)＞V∞.另外,若|x|≥R0,R0＞0,有c＜FV∞.设ε∈(0,1),因为在中{wn}n是有界的,则断言:存在Rε＞R0使得,当ε→0时,Rε→+∞且存在子列{wn},使任意n∈N得

其中

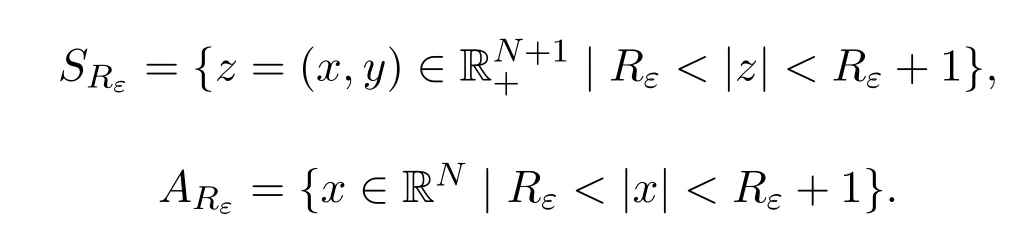
如若不然,对任何l∈N,l≥R0,存在ν(l)∈N使得,对任何n∈N,n≥ν(l)

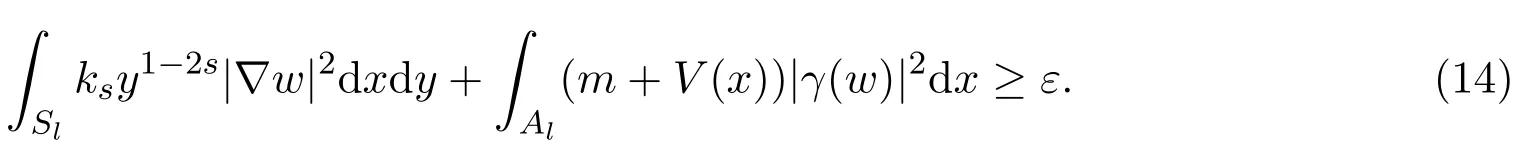
假设ν(l)是不减的,因此,对任何整数l≥R0,存在一个整数ν(l)使得,对任何n≥ν(l)有

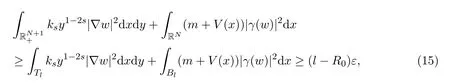
其中

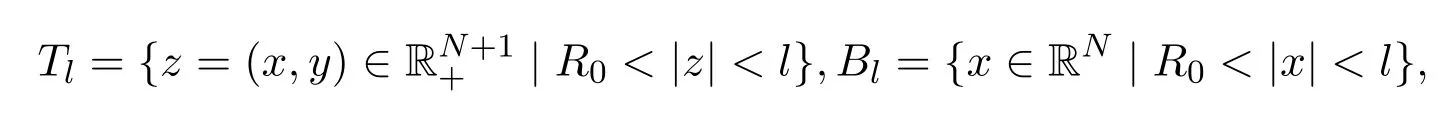
这与‖wn‖是有界矛盾.

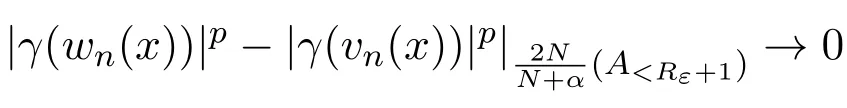
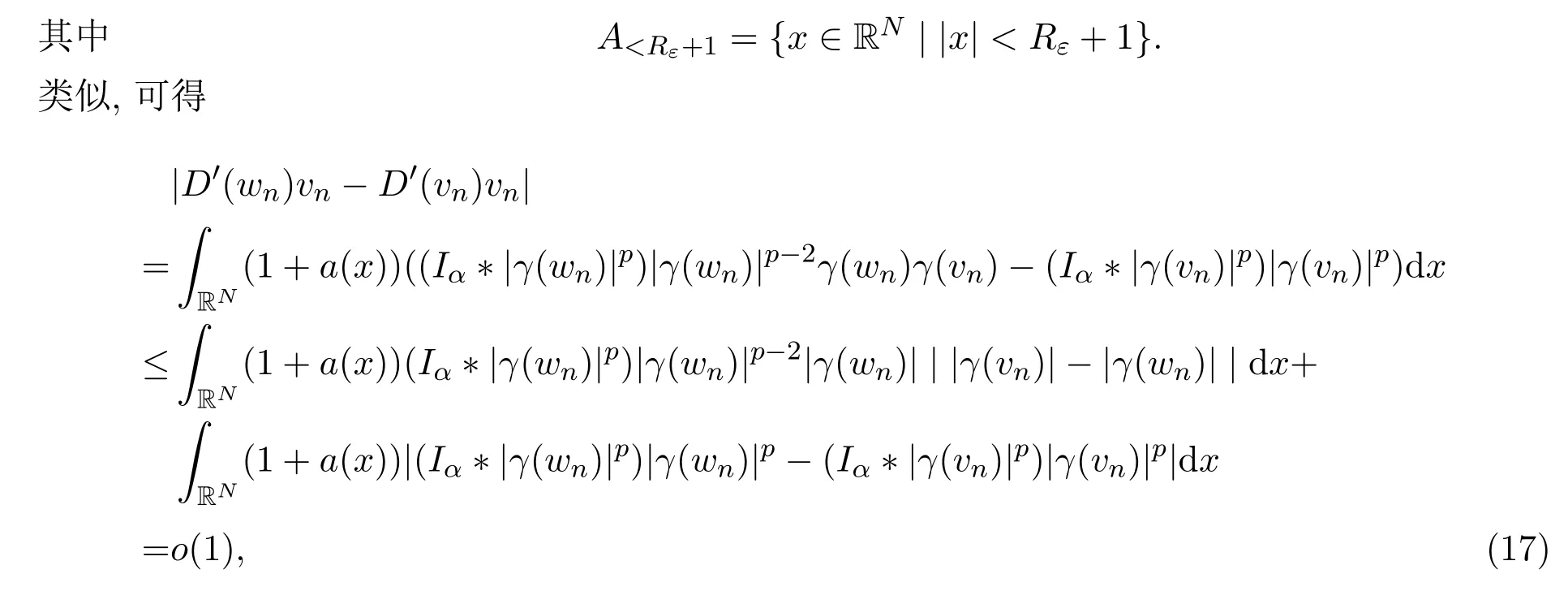
因此,据(7)和(17)可得

设un=(1−ξε)wn，又由

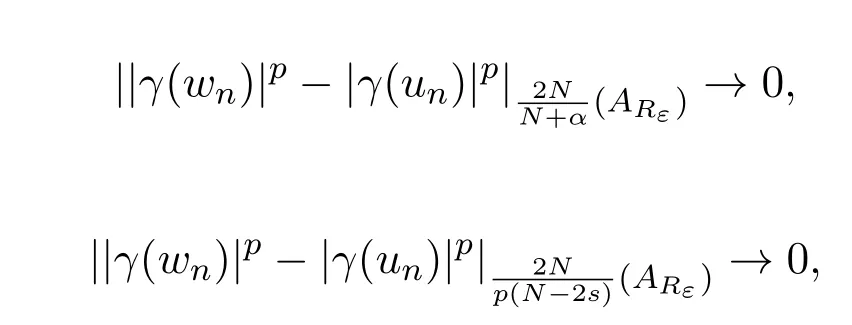
可知,当n→∞时,可得

即可得|D′(wn)un−D′(un)un|→0.当n→∞时,因此,

因此,综合(18)和(20)可得

利用(21)第一个等式可得

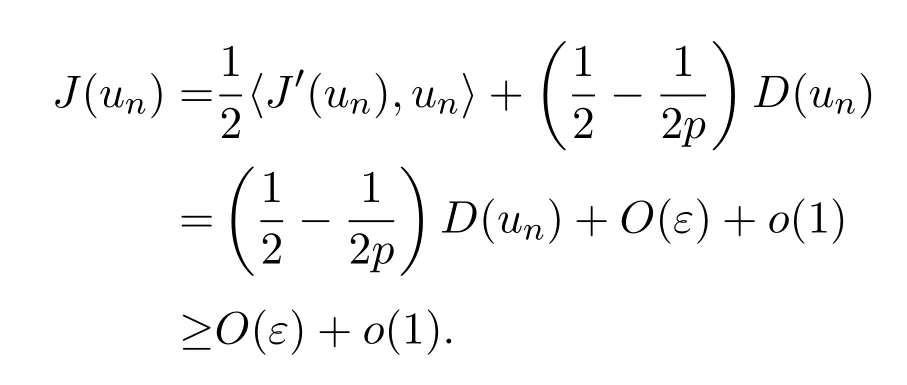
又因为对任意n,tn≥0,则

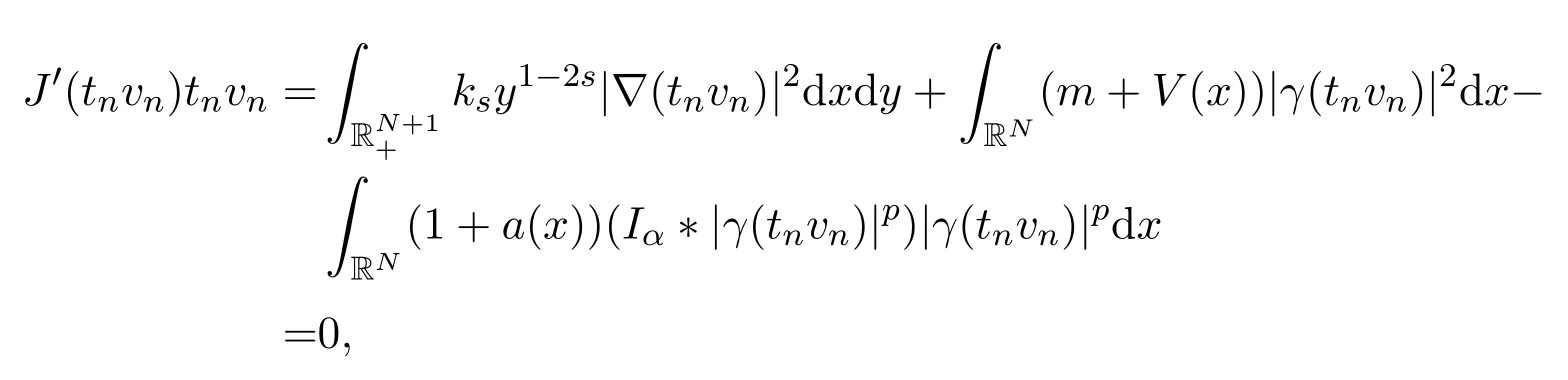
因此,据(21)第二个等式可得

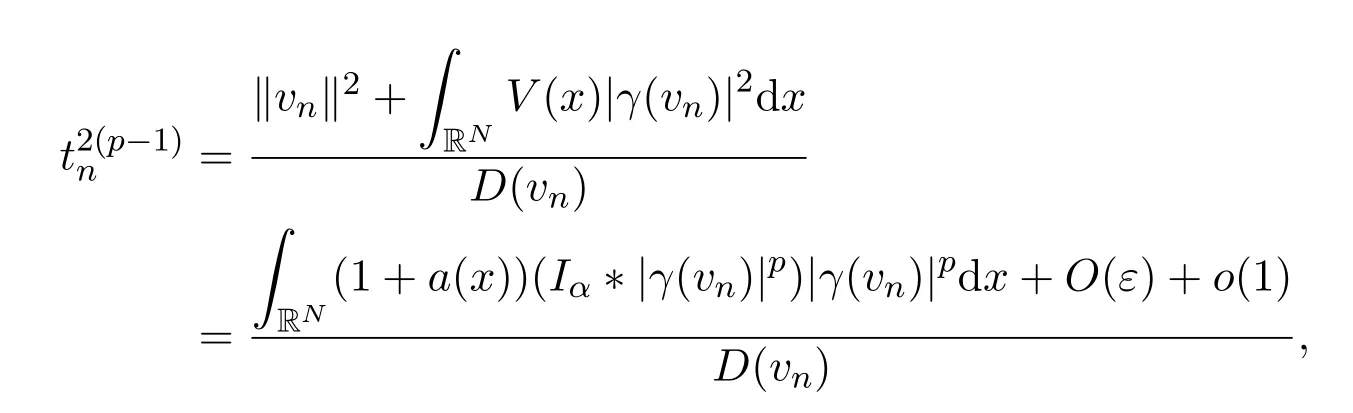
即

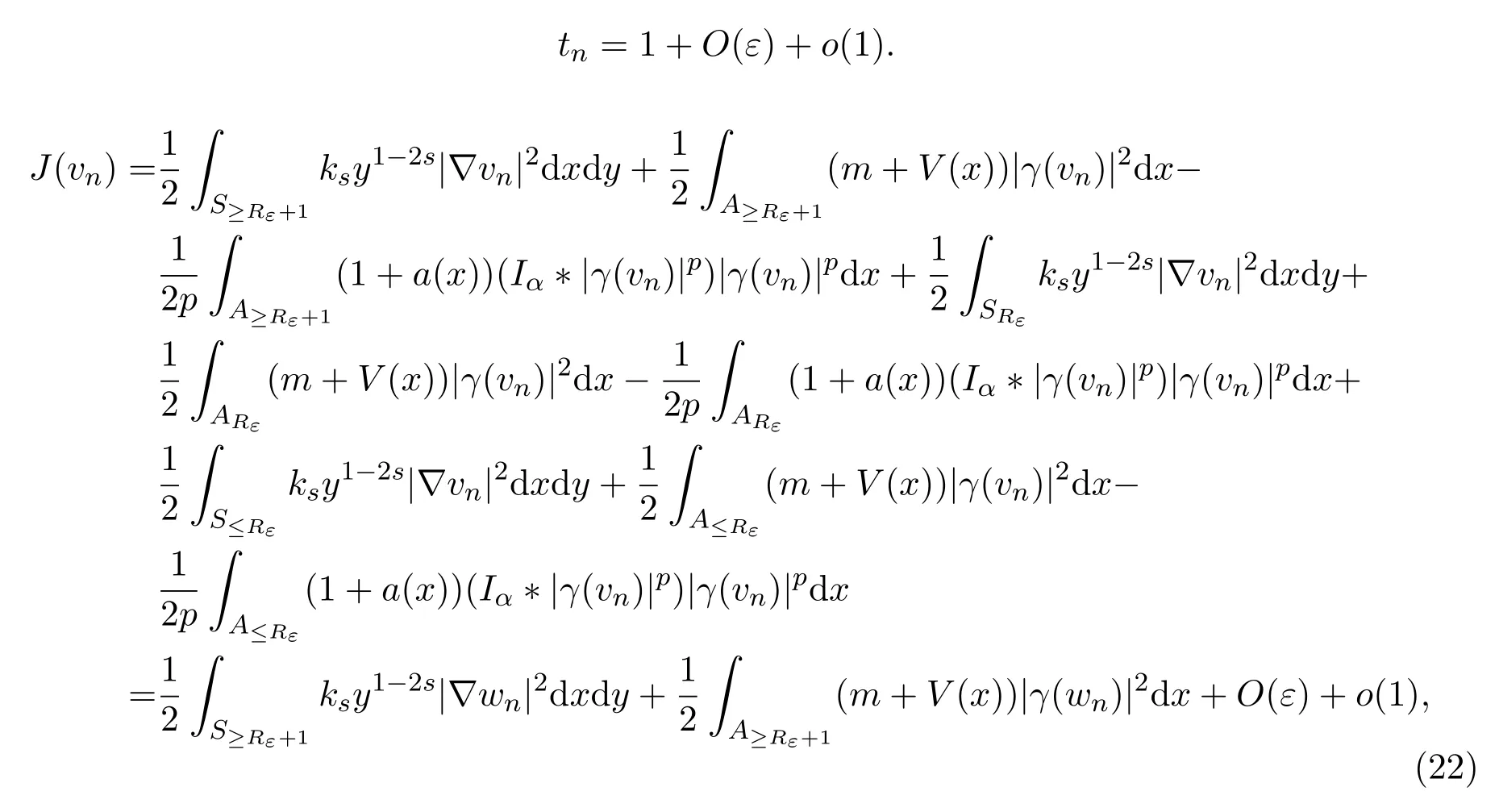
以及

这里

又据引理3.2可得

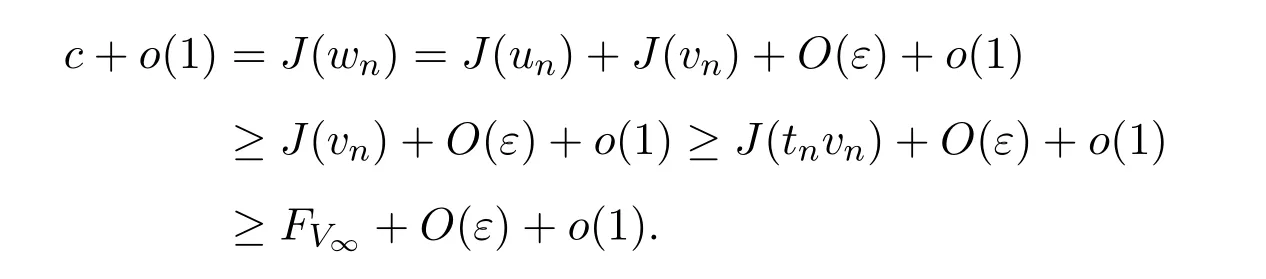
因此,可得c≥FV∞,这与假设矛盾.综上可得,c=0,且在中,当n→∞时,wn→0.

引理 4.2设{wn}n是中的一个序列,使得在中wn⇀w,则

(i)对所有,有D′(wn)u→D′(w)u;

(ii)在中存在子列,使得当n→∞时,在中,以及

,在R中,

,在中.

证明(i)由文献[4]中引理4.2,可得,当n→∞时,

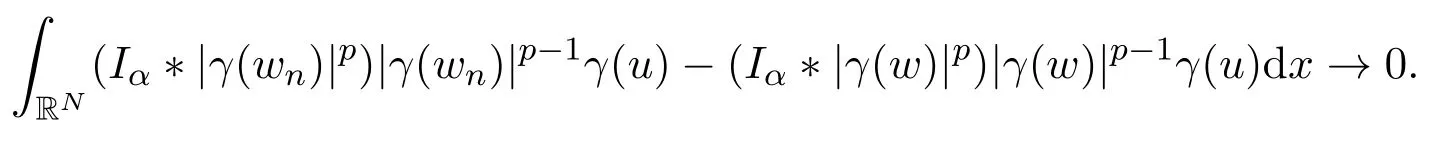
其中

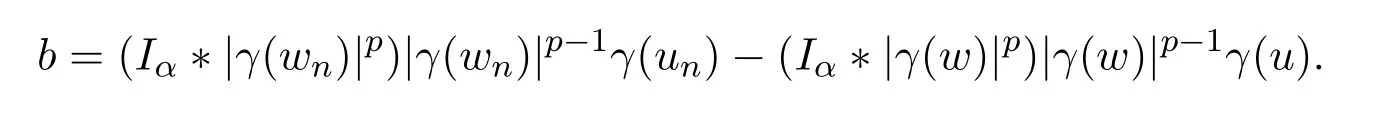
因此,当n→∞时,D′(wn)u→D′(w)u.

(ii)当n→∞时,

综上所述,可得(ii)成立.

命题 4.3当c＜FV∞时,J(w):E(RN+1+)→R满足(PS)c,其中

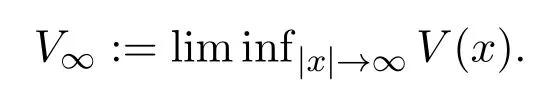
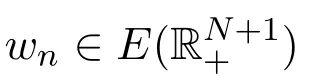
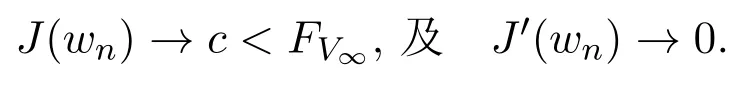
由引理4.2知,w是方程(1)的解,且在中存在序列,使得中的一个子列

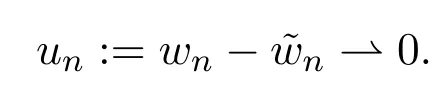
另外在RN中有

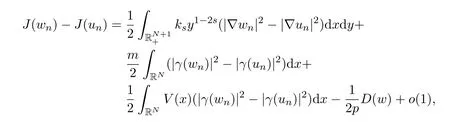
于是有

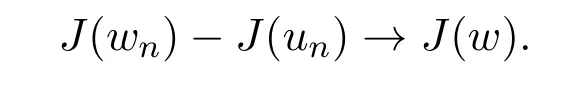
因此,又由

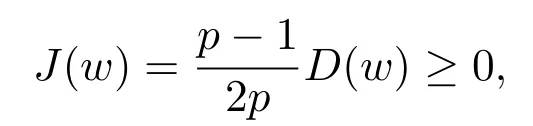
则当n→∞时,J(un)→c−J(w)≤c,及在中,J′(un)→0.再由引理 4.1知,子列{un}n在中强收敛于0,即un→0.这就推出{wn}n的子列在中,当n→∞时,有wn→w.

5 定理1.1的证明

现据引理2.1,泛函J在中满足山路引理的几何条件.另外,据命题4.3,泛函J也满足Palais-Smale条件.则据山路引理可得J至少存在一个非零临界点,

其中

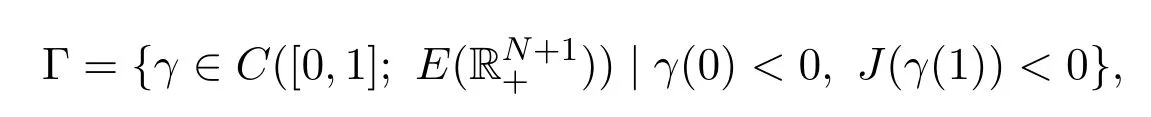
并且是方程(1)的一个弱解.

为证明w≥0.注意到,对于在上泛函J的任何临界点,映射t→J(tw)有且只有一个严格最大值点在t=1处.通过文献[9]中定理6.17可知,对所有有J(|w|)≤J(w),且对所有t＞0,,

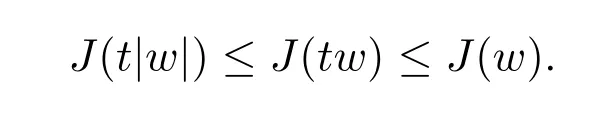
则

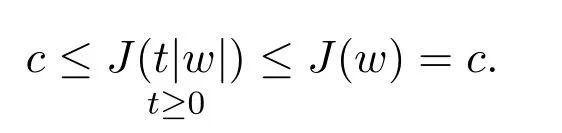
于是,我们断言|w|也是泛函J的一个临界点.否则,可以将道路t→t|w|变形为道路γ∈Γ使得对每一个t≥0,有J(γ(t))＜c,这与c的定义矛盾.因此,w必为非负的.

[1]Moroz V,Van Schaftingen J.Semi-classical states for the Choquard equation[J].Calculus of Variations and Partial Differential Equations,2015,52(1/2):199-235.

[2]Secchi S.A note on Schr¨odinger–Newton systems with decaying electric potential[J].Nonlinear Analysis:Theory,Methods Applications,2010,72(9):3842-3856.

[3]Clapp M,Salazar D.Positive and sign changing solutions to a nonlinear Choquard equation[J].Journal of Mathematical Analysis and Applications,2013,407(1):1-15.

[4]Cingolani S,Secchi S.Ground states for the pseudo-relativistic Hartree equation with external potential[J].Proceedings of the Royal Society of Edinburgh:Section A Mathematics,2015,145(1):73-90.

[5]Chen Y H,Liu C G.Ground state solutions for non-autonomous fractional Choquard equations[J].Nonlinearity,2016,29(6):1827.

[6]Caffarelli L,Silvestre L.An extension problem related to the fractional Laplacian[J].Communications in Partial Differential Equations,2007,32(8):1245-1260.

[7]Nezza E Di,Palatucci G,Valdinoci E.Hitchhiker’s guide to the fractional Sobolev spaces[J].Bulletin des Sciences Math´ematiques,2012,136(5):521-573.

[8]Zelati V C,Nolasco M.Existence of ground states for nonlinear,pseudo-relativistic Schr¨odinger equations[J].Atti della accademia nazionale dei lincei,Rendiconti lincei,Matematica e applicazion,2011,22(1):51-72.

[9]Lieb E H,Loss M.Analysis,Graduate Studies in Mathematics[M].2nd ed.USA:American Mathematical Society,2001.

Ground states for fractional Choquard equations with external potential

Liu Ruina1,Zhang Guoqing1,Liu Sanyang2
(1.College of Sciences,University of Shanghai for Science and Technology,Shanghai 200093,China;2.College of Sciences,Xidian University,Xi′an 710071,China)

We consider the following fractional Choquard equation,

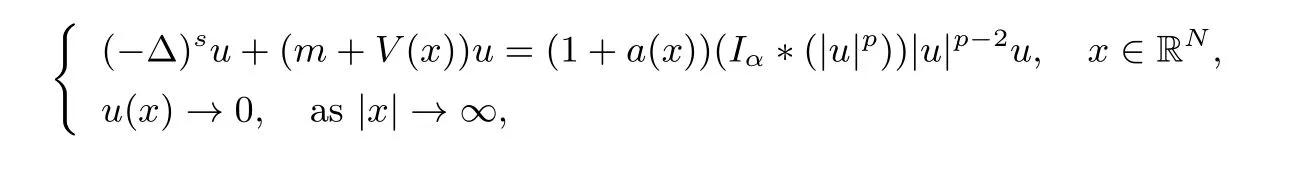
whereV(x)is a bounded external scalar function,Iαis a Riesz potential,s∈(0,1),α∈(0,N)andp∈[2,∞).Asa(x)satis fi es the appropriate condition,and does not have any symmetry condition,we obtain the existence of ground state solutions for the equation by using Nehari mainfold technique,Concentration-compactness principle and the Mountain Pass theorem.

fractional Choquard equation,external potential,ground states

2010 MSC:35J50,35J60

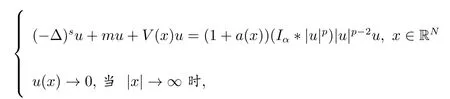
O175.25

A

1008-5513(2017)06-0585-15

10.3969/j.issn.1008-5513.2017.06.005

2017-10-18.

国家自然科学基金(11771291).

刘瑞娜(1989-),硕士生,研究方向：非线性分析,偏微分方程.