中学生数学创新思维体系建构的途径

广东省惠东县教育局教研室(516000) 汪辉

随着现代科技迅猛发展和知识经济的兴起、知识更新速度日益加快,创新将决定一个国家和民族的综合实力和竞争力.正如原总书记江泽民说“创新是一个民族进步的灵魂,是国家兴旺发达的不竭动力.”因此,在中学数学教学中,结合教材内容,刻意挖掘教材中的创新因素,渗透创新教育思想,帮助学生树立创新意识,培养创新思维,发展创新能力,建构创新思维体系.这不仅是时代对我们的客观要求,也是提高民族整体素质和培养本世纪创新人才的需要.本文旨在从“开启创新思维、诱发创新思维、培养创新思维、延续创新思维、升华创新思维”等五个方面对中学数学教学中建构学生创新思维体系的途径,做了一些具体的思考.

一、富于想象,开启创新思维.

想象是在原有表象的基础上加工改造形成新形象的思维.创新想象并不依据现在的描述或图示,而是根据一定的目的和任务,把经过改造的各个成分纳入新的体系而创新出新的完整形象的过程,其结果具有新颖性、独创性、奇特性.古希腊亚里士多德说:“想象是所有发现、发明等创造性活动的源泉.”可见,一切新活动,都是从创新想象开始,没有想象就没有任何发明创造.因此.在中学数学教学中,自觉而有意识地追求数学材料和数学事实的形象,让学生展开思维的翅膀大胆想象,能有效地开启学生的创新思维.讲扇形面积时,可将扇形想象成三角形,便获得是弧长,R为半径).求正n边形的面积,当n无限大时,将正n边形想象成圆进行近似计算.圆锥想象成由一个直角三角形绕一直角边旋转一周所形成的图形.对于某些例题、习题的分析,也可用想象获得巧妙的解法.

例如图1,两个同心圆被两条半径截得的AB弧长为6πcm,CD弧长为10πcm,且AC=12cm,求阴影部分ABCD的面积.

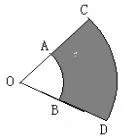
图1

此题的常规解法是:S阴影ABCD=S扇形OCD-S扇形OAB(解略)

解题后,根据图形的特征,引导学生想象成梯形模型,进行探索、分析,可得到创新的解法:以直替曲,把所求阴影部分面积看成是曲边梯形面积,便巧妙地获得新颖解法.

这种解题方法突破了常规性,既准确、快捷,同时又肯有创新性.有利于培养学生独立探索,发现和创造能力.因此,让学生冲破框框的局限,充分发挥想象,常能打破常规,另辟蹊径,获得简捷、明快、精巧的解法,从而有效地开启学生的创新思维,同时也在想象层面对学生的创新思维体系进行了构建.

二、美为媒介,诱发创新思维.

数学家阿达玛指出:“数学家的美感犹如一个筛子,缺少美感的人不会成为一个发明家.”他认为,数学美感是数学发明的真正动力.这种美感越强,数学直觉能力也就越强,数学发现与发明的才能就越大.因此,教学中凭借数学本身所赋予的审美因素,让中学生感受到数学的简洁、对称、相似、和谐、严谨、奇异等数学美.在审美情感支配下对数学美的追求,一旦题目提供的知识信息与审美主体的审美情感相吻合,就会激起审美直觉,引发联想,拓展思维空间,通过归纳、类比、猜想等推理方法,不断发现新知识,创新地解决问题,从而诱发学生的创新思维.

例已知x+2y+3z=20,x+3y+5z=31,求x+y+z的值.

分析已知条件中方程的个数少于未知数的个数,不能直接求解x、y、z的值.但仔细观察,感受到方程与未知数个数的奇异性和等式结构的和谐美感,把x+y+z看作一个整体求出,就能巧妙简洁地解决问题.

解将已知条件化为解得:x+y+z=9.

教学中,教材的很多内容,都可以通过精心设计,引导学生追求数学美感,在数学美的激发下,以美为媒,对于开拓思维,诱发学生的创新思维是非常有益的,而且也在局部与整体两方面构建了学生的创新思维体系.

三、灵活多变,培养创新思维.

思维的灵活性是创新思维的特征之一,它表现为思维敏捷,随机应变,善于全面地转换观察,分析、思考的角度,使问题出奇制胜地获解,这是创新思维的灵魂.在中学数学课堂教学中,依据教材内容有意识地引导学生从多角度、多层次、多方位去思考问题.强化各种数学思维策略变换的训练,促使学生当思维遇到障碍时,迅速进行转换,从而获取解决问题的方法,这样能防止思维僵化、拓宽思路、活化知识,有利于培养创新思维.例:引导学生探讨公式的逆应用或探讨定理的逆命题是否正确,它对于激发学生探索新知,培养学生创新思维能力具有重要意义.

例已知:二次方程(b-c)x2+(c-a)x+a-b=0(b/=c)有相等的实数根,求证:2b=a-c.

分析此题采用常规证法较困难,引导学生转换思考角度,通过观察、分析等式结构系数特征,易知此方程系数和为零的特点.便能创新地获得简捷的证法.

证明因为(b-c)+(c-a)+(a-b)=0,又因为此二次方程有相等实数根,所以两根为:x1=x2=1.由一元二次方程的根与系数关系可得:所以a-b=b-c,所以2b=a-c.

可见,引导学生善于变换思考角度,挣脱思维定势的束缚,敢于打破常规的禁锢,敢于探索创新,便能巧妙地获得简捷、独特、新颖的解法.从而有效地培养学生的创新思维能力,最大程度地在普遍性和特殊性之间建构了学生的创新思维体系.

四、大胆猜想,延续创新思维.

“猜想是人类认识中最活跃、最积极的因素,是人类理性中最富于创造的部分.有了猜想,人的认识才摆脱了消极等待的奴隶状态.”正如伟大的物理学家牛顿所说:“没有大胆的猜想,就做不出伟大的发现.”许多数学结论的发现,都是从猜想开始,然后设法加以证明.可见,猜想是创新思维的源泉,猜想是科学发现的重要途径,猜想是数学发展的强大动力.在数学问题解决的关键时刻,如果善于提出猜想,将有利于解题方向及解题思路的形成.因此,在中学数学教学中,要根据教材编写的特点和学生的认识规律,引导学生开动脑筋,激发学生猜想的欲望,培养学生猜想的兴趣,鼓励学生勤于观察,大胆地提出猜想,允许学生提出各种“异议”,启发学生进行多向猜测、多向思考.对发展学生的猜想能力,实现认识能力的飞跃和突破,从而发展、延伸学生的创新潜能.

例已知(z-x)2-4(x-y)(y-z)=0,求证:x+z=2y.

将原方程展开得x2+2xz-4xy+z2-4yz+4y2=0,引导学生整体考察,凭直觉猜想到可将原方程化为关于x的一元二次方程,从而获得通过解关于x的方程就可得出所要证明的结论.

证明由已知等式得:x2+2xz-4xy+z2-4yz+4y2=0,故有:x2+2(z-2y)x+(z-2y)2=0,于是有(x+z-2y)2=0,故x+z=2y.

再进一步引导学生探索,得出又一新证法.通过整体观察原方程左边的结构与一元二次方程的根的判别式b2-4ac非常相似,从而猜想此题可以构造一元二次方程来求解.于是可把已知条件看作是t的二次方程(x-y)t2+(z-x)t+(y-z)=0有等根的条件.进而观察到方程左边的系数之和为零,故方程的两个根均为1,于是由一元二次方程根与系数的关系得:t1·t2=1,即所以x+z=2y.

可见,精心安排教材,设计教法,引导学生开展各种归纳、类比等丰富多彩的探索活动,鼓励学生积极猜想,对发展、延续学生创新思维具有积极实践意义,在大胆猜想中构建了学生的创新思维体系.

五、打破常规,升华创新思维.

思维的创新性是指思维活动的内容、途径和方法的自主创新程度.它是思维中最可贵的品质,包含有新颖、独特、创造等因素.它表现为思维的不寻常规,不拘常法,不落俗套,寻求变异,勇于创造.因此,中学教师在教学中要注意引导学生积极探索、尝试、不断创新,不断激起学生强烈的求知欲,不断鼓励学生创造思维的萌芽、探究目标、发现隐含条件,不拘常规地以前所未有的思路去探索、尝试问题的解,以不同的崭新的角度去思考问题.使学生的思维纵横驰骋,创造力得到充分的发挥,从而能有效地升华学生思维的创新性.

例如图2,在矩形ABCD中,AB=a,BC=b,M是BC的中点,DE⊥AM,E是垂足,求证:

图2

本题常规解法是应用相似三角形的判定和性质来证明,先证得△ABM～△DEA,再利用相似三角形的性质,本题便可得证,这是一般方法,在此基础上,还应启发引导学生再探索尝试,另辟蹊径得出别开生面的证法.

证明连结DM,如图3,因为故而所以

图3

再进一步引导学生探索,得出又一新证法.如图4:延长AM交DC的延长线于F,易证△ABM△CFM,则△ADF的面积与矩形ABCD的面积相等,从而得出结论.

图4

在整个解题过程中,学生始终处于一种积极探索、创造的状态,根据已学过知识,不断探索、产生“顿捂”或“触类旁通”,创造性地解决了问题,使学生在不断探究中构建了创新思维体系.

综上可知,中学数学课堂中构建学生创新思维体系的关键在于酝酿它的发生机制.因此,教学中教师要从上述五个方面着手深入挖掘,研究教材中的创新因素,从多渠道、多层次积极有地开展创新活动,从而最大限度去开发学生的创新潜能,培养创新思维能力、建构创新思维体系,为进一步提高中学数学课堂教学效率奠定坚实基础.当然,创新思维体系的建构是一项长期艰巨的任务,有待于我们进一步的探讨和开拓.

[1]《数学思维方法》傅学顺、王屏山,暨南大学出版社.

[2]《课程·教材·教法》.人民教育出版社.2003.3.

[3]《创新教学探索全书》.兴旺主编.湖南教育出版社.1999年版.