The{P,k+1}-re flexive Solution to System of Matrix Equations AX=C,XB=D
CAO Nan-bin,ZHANG Yu-ping
(1.Collage of Mathematics and Information Science,Hebei Normal University,Shijiazhuang 050016,China;2.School of Mathematics and Science,Hebei GEO University,Shijiazhuang 050031,China)
§1. Introduction
Throughout this paper,Rm×n,Cm×nand Un×nstand for the sets of all m×n real matrices,the sets of all m×n complex matrices and n×n unitary matrices,respectively.For A∈Cm×n,A∗,r(A),tr(A),kAk represent the conjugate transpose,the rank,the trace and the Frobenius norm of matrix A,respectively.Fordenotes the inner product of A and B.Therefore,Cm×nis a complete inner product space and the norm of a matrix generated by the inner product is the Frobenius norm,i.e.,And A†denotes the Moore-Penrose inverse,namely,the unique matrix X,that satis fies the following four Penrose conditions,
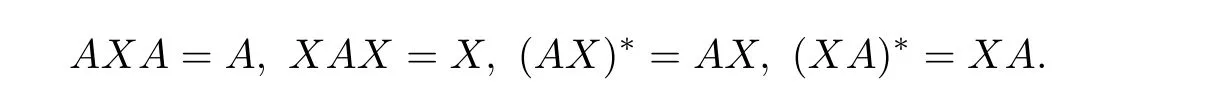
Let Ikbe identity matrix of size k,and Jkcross-identity matrix of size k having the elements 1 along the southwest-northeast diagonal and the remaining elements being zeros.The symbol Om×nis the m×n matrix of all zeros entries(if no confusion occurs,we will omit the subscript).
A matrix P ∈ Cn×nis called Hermitian and{k+1}-potent matrix if Pk+1=P=P∗.
De finition 1Let P ∈ Cn×nbe a Hermitian and{k+1}-potent matrix,we say that the matrix X ∈Cn×nis{P,k+1}-re flexive(anti-re flexive)if PXP=X(PXP= −X).
Obviously,the centro-symmetric and centro-skew matrices(when P=Jn),re flexive and antire flexive matrices(when P is Hermitian involution),are the natural extensions of the{P,k+1}-re flexive and the anti-re flexive matrices,respectively.These kinds of matrices play important roles in information theory,linear system theory,linear estimation theory,numerical analysis theory,etc.,(see,[1-3]).More generally,in[4],Herrero and Thome have obtained the{P,k+1}-re flexive and the anti-re flexive solutions to the matrix equation AXB=C.
Investigating the classical system of matrix equations

has attracted many author0s attention.For instance,in[5],Cecioni gave the necessary and sufficient conditions for the consistency of(1),in[6-7],Chu and Mitra derived an expression for the general solution by using singular value decomposition of a matrix and generalized inverses of matrices,respectively.Moreover,many results have been obtained about the system(1)with various constraints,such as bisymmetric,Hermitian,positive semi-de finite,re flexive,and generalized re flexive solutions,and so on(see,[8-19]).To our knowledge,so far there has been little investigation of the{P,k+1}-re flexive and the anti-re flexive solution of(1).
Motivated by the work mentioned above,we investigate the{P,k+1}-re flexive and antire flexive solutions of(1).We also consider the optimal approximation problem,
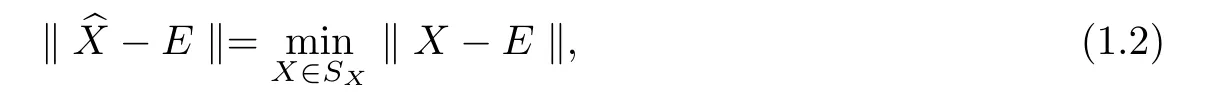
where E is a given matrix in Cn×nand SXthe set of all{P,k+1}-re flexive(anti-re flexive)solutions of(1).In many case the system(1)has not{P,k+1}-re flexive(anti-re flexive)solution,hence we need to further study its least squares solution,which can be described as follows:Let PCn×n(APCn×n)denote the set of all{P,k+1}-re flexive(anti-re flexive)matrices in Cn×n,find X such that
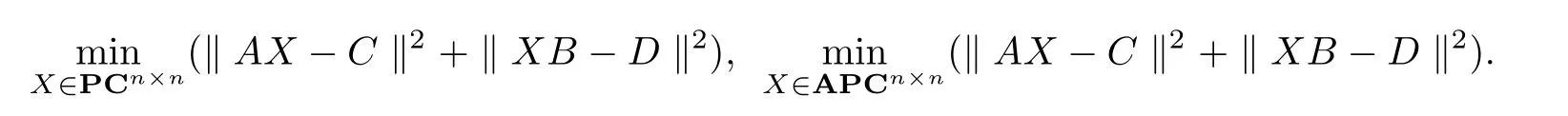
In Section 2,we present necessary and sufficient conditions for the existence of the{P,k+1}-re flexive(anti-re flexive)solution of(1)and give an expression of this solution when the solvability conditions are met.In Section 3,we derive an optimal approximation solution of(2).In Section 4,we provide the least squares{P,k+1}-re flexive(anti-re flexive)solution of(1).
§2. The{P,k+1}-re flexive(anti-re flexive)Solution of(1)
The following lemma derived from[4]characterizes the Hermitian and{k+1}-potent matrices.
Lemma 1Let P ∈ Cn×nbe Hermitian,then P is{k+1}-potent matrix if and only if P is idempotent(i.e.,P2=P)when k is odd,or tripotent(i.e.,P3=P)when k is even.Moreover,there exists U ∈Un×n,such that
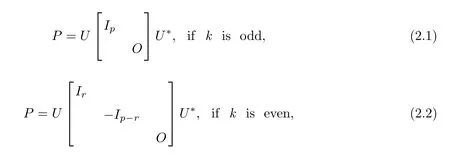
where p=r(P).
Throughout this paper,we always assume that the Hermitian and{k+1}-potent matrix P is fixed which is given by(2.1)and(2.2).
From Lemma 1,we can see that the general{k+1}-potent matrix P can be reduced to only two simpler cases:P2=P(i.e.,k=1)and P3=P(i.e.,k=2).Consequently,we will discuss our problems through{P,2}-re flexive(anti-re flexive)and{P,3}-re flexive(anti-re flexive)constraints.
Note that De finition 1 and Lemma 1,we can easily verify that the following conclusions are true.
Lemma 2Let X ∈ Cn×nis{P,2}-re flexive if and only if

or{P,3}-re flexive if and only if

where
Assume that P is idempotent(i.e.,k=1)and PXP=−X,then by pre-multiplying and post-multiplying it by P,we get PXP=−PXP,which implies that PXP=O and thus,X=O.In this case,the system of matrix equations(1)is inconsistent whenConsequently,for the anti-re flexive case,we only consider the{P,3}-anti-re flexive solution.
From(2.2),X ∈Cn×nis{P,3}-anti-re flexive if and only if it can be written as
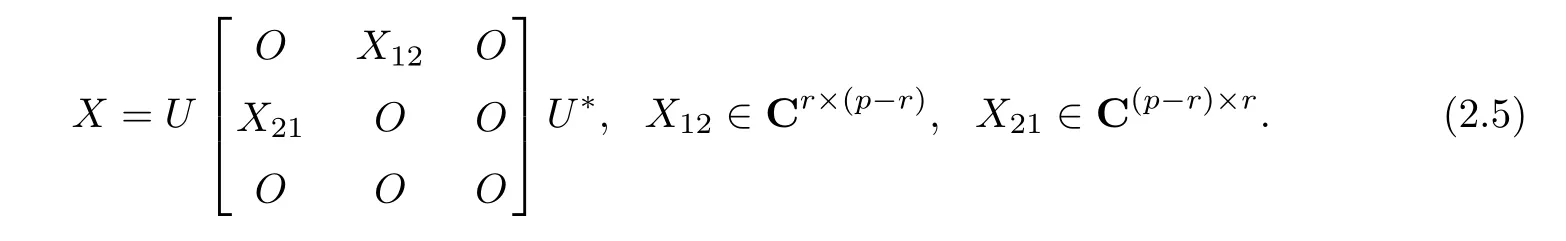
In addition,the following lemma is well-known(see,[10]).
Lemma 3The system of matrix equations(1)is consistent for unknown matrix X if and only if

In this case,the general solution is
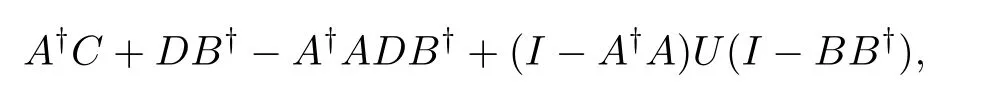
where U is arbitrary.
2.1 The{P,2}-re flexive Solution of(1)
Let P ∈ Cn×nbe Hermitian and{k+1}-potent matrix as given in(1),and partition

where.Then,we have the following result.
Theorem 1Given A,C ∈Cm×n,B,D ∈Cn×k.Let A1,C1,B1,D1be de fined in(2.6),then the system of matrix equations(1)is consistent for{P,2}-re flexive X if and only if

In this case,the general solution is

where U1∈ Cp×pis arbitrary.
ProofFrom the formula(2.3)in Lemma 2,we deduce that(1)is consistent for{P,2}-re flexive X can be equivalently converted into solving the following matrix equations
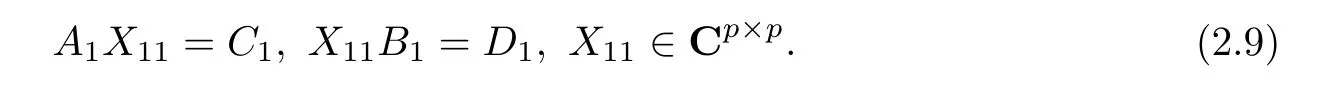
It follows from Lemma 3 that(2.9)is consistent if and only if(2.7)and the expression of the general solution is(2.8).
2.2 The{P,3}-re flexive Solution of(1)
Let P ∈ Cn×nbe Hermitian and{k+1}-potent matrix as given in(2.2)and partition

where
Then,we have the following result.
Theorem 2Given A,C ∈Cm×n,B,D ∈Cn×k.Let A1,A2,C1,C2,B1,B2,D1,D2be de fined in(2.10),then the system of matrix equations(1)is consistent for{P,3}-re flexive X if and only if

In this case,the general solution is
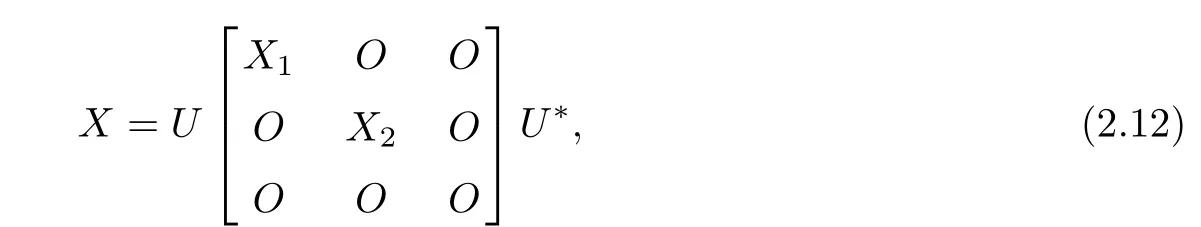
whereare arbitrary.
ProofFrom the formula(2.4)in Lemma 2,we deduce that(1)is consistent for{P,3}-re flexive X can be equivalently converted into solving the following matrix equations
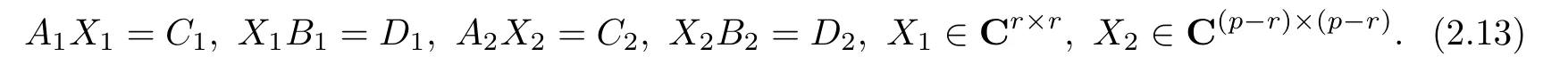
It follows from Lemma 3 that(2.13)is consistent if and only if(2.11),and the expression of the general solution is(2.12).
Remark 1From(2.5),the key to solve{P,3}-anti-re flexive constraint solution of(1)is to find the solution of the system of matrix equations

Similar to Theorem 2,the conclusion is omitted.
§3.Solution to the Optimal Approximation Problem
This section solves the optimal approximation problem,i.e.,suppose that the solvability conditions of matrix equation(1)in Theorem 1,and Theorem 2 hold,then we derive the following results.From AX=C it follows that C=AX=AA†AX=AA†C and D=DB†B.
Lemma 4[20]Suppose thatand Γ ∈ Rm×m,where∆2= ∆ = ∆Tand Γ2= Γ = ΓT.Then

if and only if∆(A−D)Γ =0,in which case,

By Lemma 4,letthen the procrustes problem

has a solution if and only if
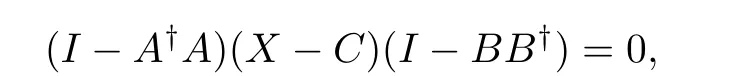
that is,the solution can be expressed as

whereare arbitrary matrices.
Theorem 3Let SXbe the set of all{P,2}-re flexive solutions to(1)as in Theorem 1 and E is a given matrix in Cn×n.Partition

Then,

has a only solutionwhich can be expressed as

ProofIt is easy to verify that the solution set SXis a closed and convex set in matrix space Cn×nunder Frobenius norm,so the solution to the approximation problem is unique.Note that(2.8),(3.2),and the unitary invariance of the Frobenius norm,we get


By(3.1),we have

if and only ifwithbeing arbitrary is the solution of the above procrustes problem.
Theorem 4Let SXbe the set of all{P,3}-re flexive solutions to(1)as in Theorem 2,and E is a given matrix in Cn×n.Partition

Then,

has a only solutionwhich can be expressed as
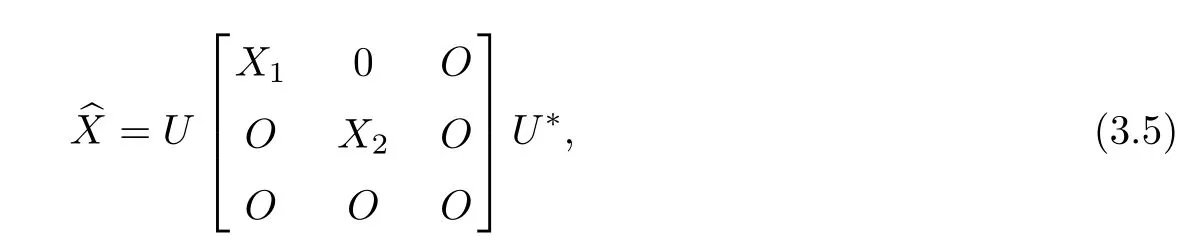
where
ProofSimilar to Theorem 3,the proof is omitted.
§4. The Least Squares{P,k+1}-re flexive(anti-re flexive)Solution to(1)
Lemma 5[9]Given E,F ∈ Cm×n,Ω1=diag(a1,···,am),Ω2=diag(b1,···,bn),ai>0(i=1,···,m),bj>0(j=1,···,n).Then there exists a unique matrixsuch that

andcan be expressed as
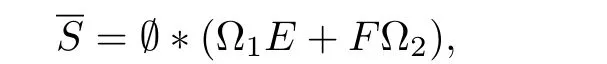
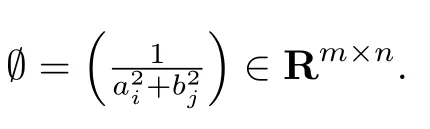

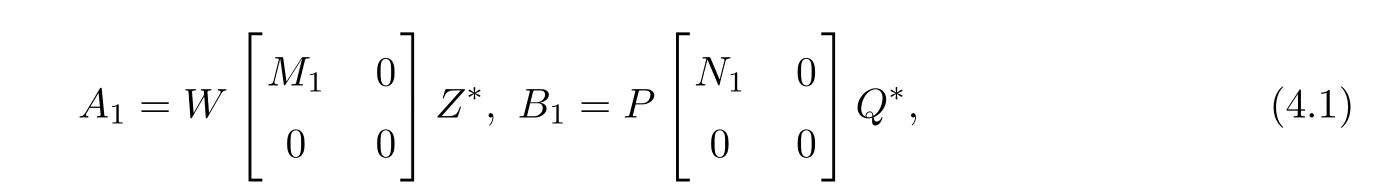
whereand Q=[Q1,Q2]∈ Ck×kare unitary matrices,Then X ∈ SLcan be expressed as
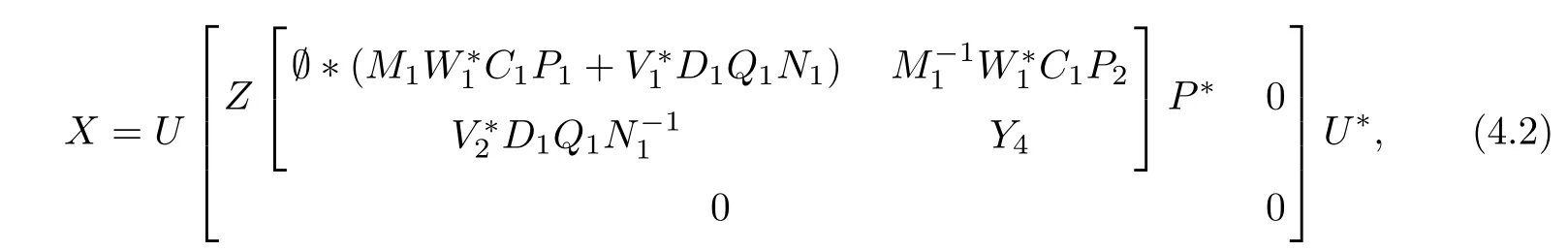
ProofIt yields from(4.1)that

Assume that
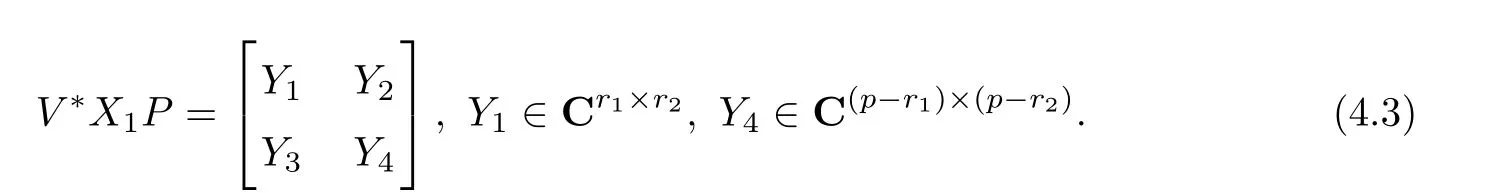
Then we have
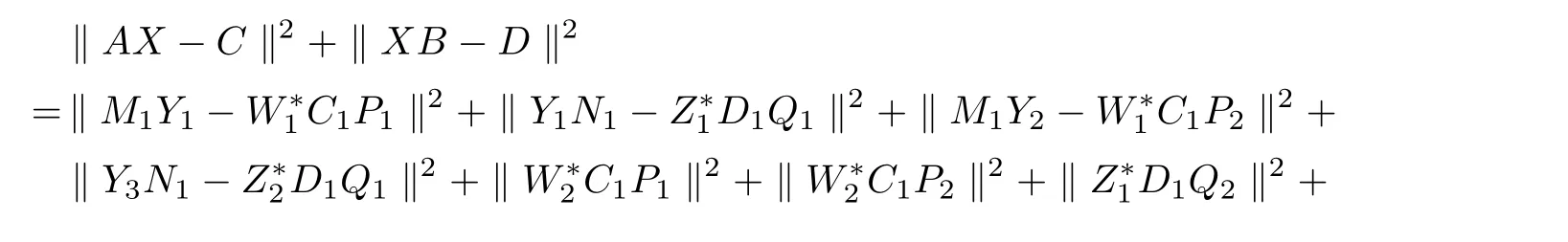

Hence
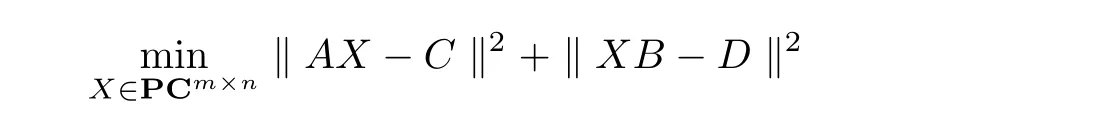
is solvable if and only if there exist Y1,Y2,Y3such that
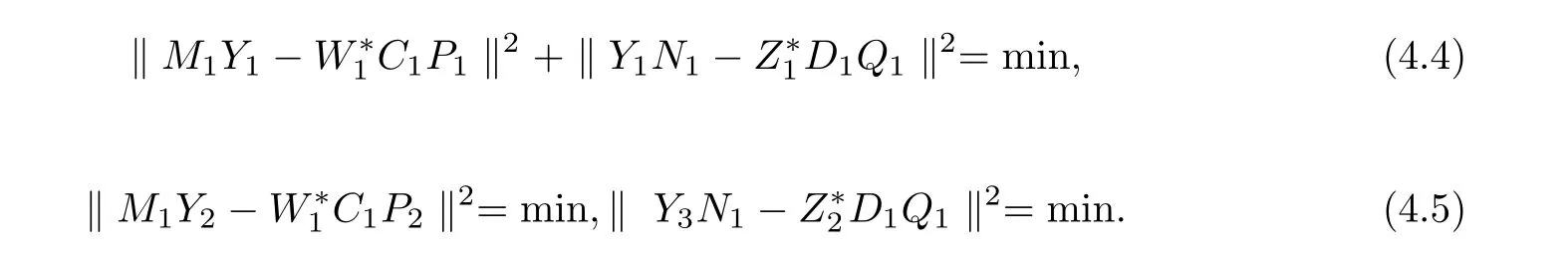
It follows from(4.4)and(4.5)that
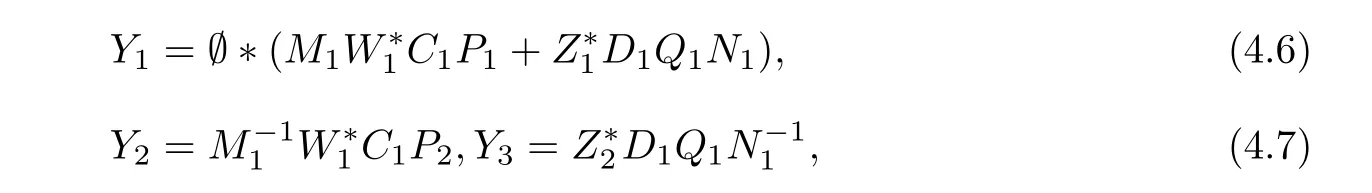
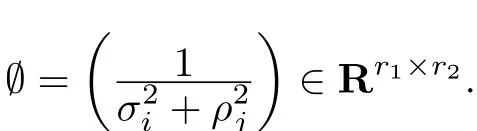
Theorem 6Let SXbe the set of all least squares{P,2}-re flexive solutions to(1)as in Theorem 5 and E is a given matrix in Cn×n.Partition

Partition

Then,

has a only solutionwhich can be expressed as

ProofIt is easy to verify that the solution set SXis a closed and convex set in matrix space Cn×nunder Frobenius norm,so the solution to the approximation problem is unique.Note that(4.2),(4.8),(4.9)and the unitary invariance of the Frobenius norm,we get
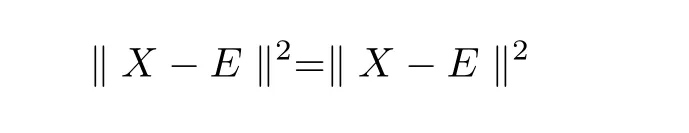

It is easy to know(4.10)is the solution of the above approximation problem.
Remark 2The{P,3}-re flexive and anti-re flexive constraint least squares problem can be reduced similar to Theorem 5 and Theorem 6,the conclusion is omitted here.
[1]ANDREW A L.Centrosymmetric matrices[J].SIAM Rev,1998,40:697-698.
[2]WANG Qing-wen,SUN Jian-hua,LI Shang-zhi.Consistency for bi(skew)symmetric solutions to systems of generalized Sylvester equations over a finite central algebra[J].Linear Algebra Appl,2002,353:169-182.
[3]CHEN H C.Generalized re flexive matrices:special properties and applications[J].SIAM J Matrix Anal Appl,1998,19(1):140-153.
[4]HERRERO A,THOME N.Using the GSVD and the lifting technique to find{P,k+1}re flexive and anti-re flexive solutions of AXB=C[J].Appl Math Lett,2011,24:1130-1141.
[5]CECIONI F.Sopra operazioni algebriche[J].Ann Scuola Norm Sup Pisa Sci Fis Mat,1910,11:17-20.
[6]CHU W E.Singular value and generalized singular value decomposition and the solution of linear matrix equations[J].Linear Algebra Appl,1987,88/89:83-98.
[7]MITRA S K.A pair of simultaneous linear matrix equations A1XB1=C1,A2XB2=C2and a matrix programming problem[J].Linear Algebra Appl,1990,131:107-123.
[8]WANG Qing-wen,WANG De-sheng.A further study of the system of matrix equations over a skew field[J].Chin Quart J of Math,1994,9(4):22-30.
[9]CHANG Hai-xia,WANG Qing-wen,SONG Guang-jing.(R,S)-conjugate solution to a pair of linear matrix equations[J].Appl Math Comput,2010,217:73-82.
[10]DAJIĆ A,KOLIHA J J.Equations ax=c and xb=d in rings and rings with involution with applications to Hilbert space operators[J].Linear Algebra Appl,2008,429:1779-1809.
[11]DAJIĆ A,KOLIHA J J.Positive solutions to the equations AX=C and XB=D for Hilbert space operators[J].J Math Anal Appl,2007,333:567-576.
[12]DONG Chang-zhou,WANG Qing-wen,ZHANG Yu-ping.The common positive solution to adjointable operator equations with an application[J].J Math Anal Appl,2012,396:670-679.
[13]FANG Xiao-chun,YU Jing,YAO Hong-liang.Solutions to operator equations on Hilbert C∗-modules[J].Linear Algebra Appl,2009,431:2142-2153.
[14]QIN Jian-guo,SONG Guang-ai.The general and centro(kewsy)symmetric solutions to a system of matrix equations over an arbitrary skew field[J].Chin Quart J of Math,2006,21(1):66-70.
[15]KYRCHEI I.Analogs of Cramer0s rule for the minimum norm least squares solutions of some matrix equations[J].Appl Math Comput,2012,218:6375-6384.
[16]LI Fan-liang,HU Xi-yan,ZHANG Lei.The generalized re flexive solution for a class of matrix equations(AX=C,XB=D)[J].Acta Math Scientia,2008,28B:185-193.
[17]WANG Qing-wen,DONG Chang-zhou.The positive solution to a system of adjointable operator equations over Hilbert C*-modules[J].Linear Algebra Appl,2010,433:1481-1489.
[18]XU Qing-xiang.Common hermitian and positive solutions to the adjointable operator equations AX=C,XB=D[J].Linear Algebra Appl,2008,429:1-11.
[19]ZHNG Zhong-zhi,HU Xi-yan,ZHANG Lei.On the Hermitian-generalized Hamiltonian solutions of linear mattrix equations[J].SIAM J Matrix Anal Appl,2005,27:294-303.
[20]TRENCH W F.Inverse eigenproblems and associated approximation problems for matrices with generalized symmetry or skew symmetry[J].Linear Algebra Appl,2004,380:199-211.
 Chinese Quarterly Journal of Mathematics2018年1期
Chinese Quarterly Journal of Mathematics2018年1期
- Chinese Quarterly Journal of Mathematics的其它文章
- Common Fixed Point Results for Quasi-contractions Involving Altering Distance Functions in Ordered Cone Metric Spaces
- Some Generalized Normal Subgroups and p-nilpotency of Finite Groups
- The Growth Order of Solutions of Systems Complex Di ff erence Equations
- The Credibility Estimators under MLINEX Loss Function
- Implicative Pseudo Valuations on Hoops
- An Elliptic Gradient Estimate for A Non-homogeneous Heat Equation on Complete Noncompact Manifolds
