The Credibility Estimators under MLINEX Loss Function
(School of Science,Nanjing University of Science and Technology,Nanjing 210094,China)
§1. Introduction
In insurance practice,credibility theory has been widely used in commercial property of liability insurance and group heath or life insurance.The well-known credibility formulas are written as a weighted sum of the average experience of the policyholder and the average of the entire collection of policyholders.These formulas are easy to understand and simple to apply due to their linear properties.The modern credibility theory is believed to be attributed to the remarkable contribution by Bühlmann[1].He is the first one that based the distribution free credibility theory on modern Bayes statistics.For the recent detailed introduction,one can see Bühlmann and Gisler[2].
In classical decision theory,the loss function usually focuses on precision of estimation.However,the use of symmetric loss functions,such as quadratic loss function,may be inappropriate,see,for example,Varian[3],Berger[4],Ferguson[5],Zellner[6].Lin[7]used Entropy loss function to study the parameter estimations of Rayleigh distribution.Credibility estimator based on symmetric loss functions usually leads to very high maluses.To overcome this problem,using asymmetric loss functions in building credibility estimator is considered.That is,for a policyholder,”paying too much” is more serious than ”not paying enough”.In the loss functions,overcharges should be penalized more than undercharges to satisfy the policy-holders.Wen[8]established Bayes premium and two forms of credibility premiums under generalized weighted loss functions and discussed the consistency of these premiums.Wen[9]proposed a new from of credibility estimators with multiple contracts for the generalized weighted premiums and estimated the structure parameters.Kang[10]studied the empirical Bayes estimation for the parameter of the two-dimensional one side truncated distribution families by using the LINEX loss function.Then,Wen[11]discussed the single contract credibility model under LINEX loss function.Podder[12]introduced a modi fied linear exponential(MLINEX)loss function as
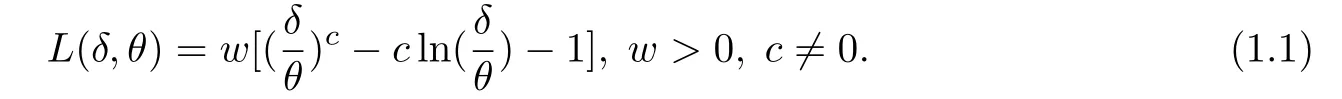
where θ is a unknown parameter and δ is the estimator of θ to be determined by minimizing this loss function in certain sense.MLINEX is a useful asymmetric loss function.Many researchers have discussed some Bayesian estimation problems under this loss function,such as Dey[13],Rahman[14]and others.Ifthen L(δ,θ)=0,writingthe relative error L(R)is minimized at R=1.If we write D=lnR=lnδ−lnθ,then L(R)can be expressed as the same form of LINEX loss function.

The property of a MLINEX function is useful in building a credibility estimator.Inspired by these papers,we aim at extending credibility estimator under MLINEX loss function.The rest of the paper is arranged as follows.Section 2 derives the collective premium and Bayes premium for MLINEX loss function.In section 3,the inhomogeneous and homogeneous credibility estimators with multiple contracts are built.Finally,the estimations of the structure parameters and a numerical example are investigated.
§2.The Premiums under the MLINEX Loss Function
In classical credibility theory,the risk X can be identi fied by a risk parameter Θ,which is an unobservable random variable with distribution π(θ).Given Θ = θ,X1,···,Xn,Xn+1are independent and identically distributed copies of X,following the common distribution F(x,θ).Let h(Θ)be a function of Θ.We use h(Θ)to estimate the future claim Xn+1by minimizing the expected lossThen the optimal premium for Xn+1under MLINEX loss function is given by
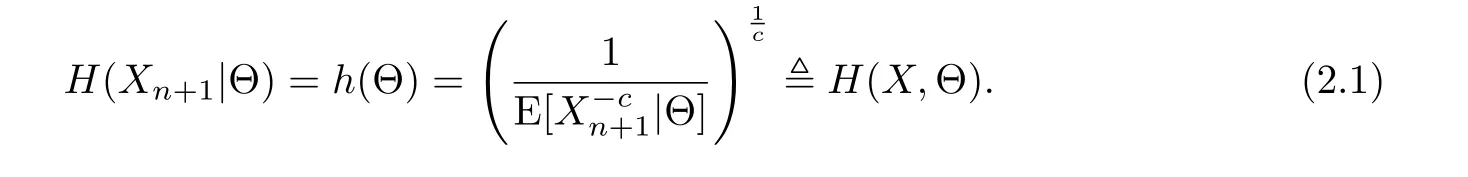
wheredenotes “de fined by”.If the risk parameter Θ is known,the premium H(X,Θ)will be the most adaptive premium for the risk X to charge under MLINEX loss function.However,the risk parameter Θ is generally unknown in practice and hence H(X,Θ)is also unknown and needs to be estimated based on the samplesDenote by Ψ the class of all measurable functions ofThe predictor of Xn+1,denoted byis such that

We can find the similar result in Wen[8]or Heilmann[15]also.
Theorem 2.1Given Θ,X1,···,Xn,Xn+1are independent and identically distributed.Under the expected loss function given by(1),the optimal estimator of Xn+1based on the sampleis

which is called Bayes premium of Xn+1.
ProofFrom the Bayes theorem,we need to solve the following problem
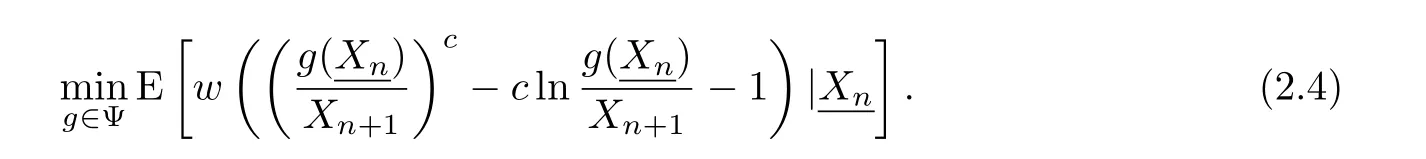
Let
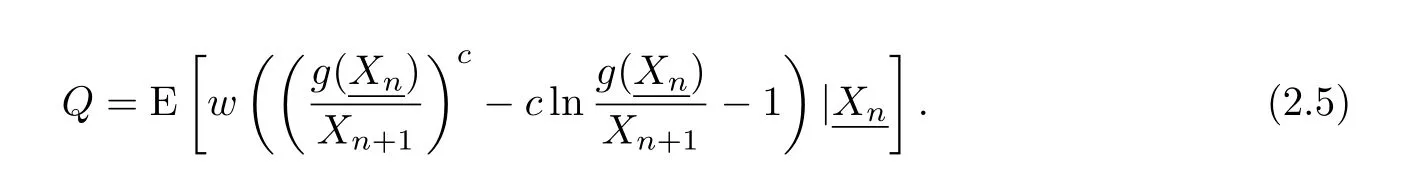
then di ff erentiate Q with respect to g and let the derivation be zeros,we get

Hence,
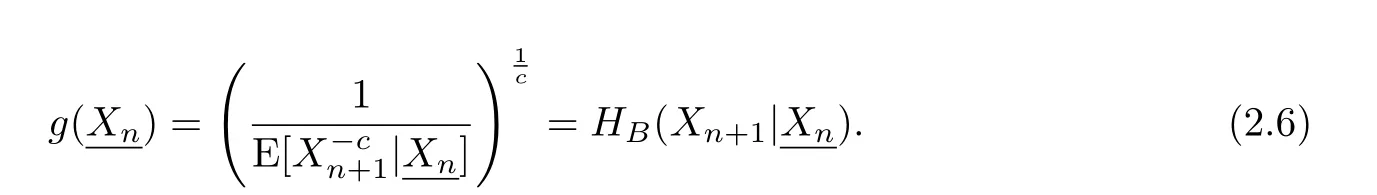
However,in order to calculatethe joint distribution of the random variables involved need to be completely speci fied and the Bayes premiumcan not be solved explicitly in most insurance practice.Notice thatanalogy to the classical credibility theory,we firstly construct the estimator ofby solving the following optimization problem



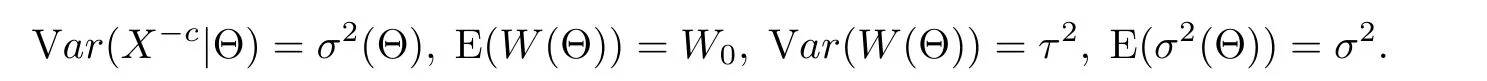
By solving(2.7),we derive the following theorem.
Theorem 2.2Under assumptions and notations above,the credibility estimator of H(X,Θ)is given by

whereis the so-called credibility factor.
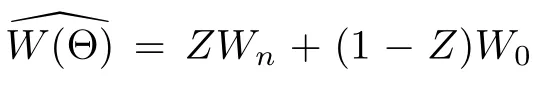

Writedi ff erentiate P with respect to b1and let the derivation be 0,then we get
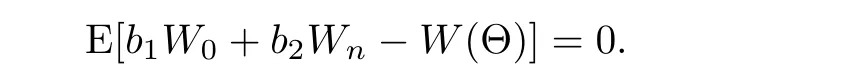


Inserting(2.10)in P,it gives P=E[W0−W(Θ)+b2(Wn−W0)]2.We di ff erentiate P with respect to b2and let the derivative be 0,and get

Then

Notice that
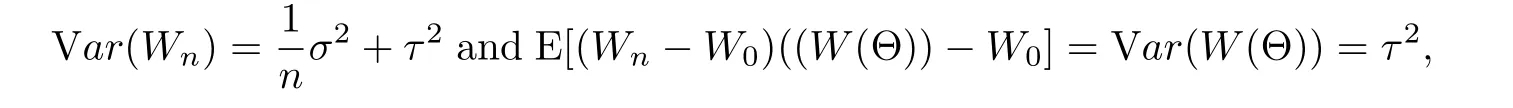
we obtain
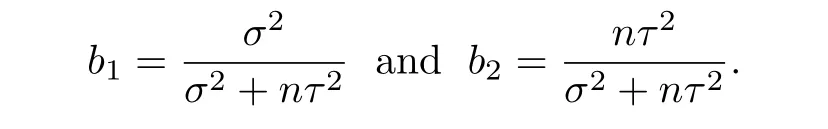
Therefore

So the credibility estimator of risk premium H(X,Θ)is

Remark 2.1If n→∞,the Z→1,and n→0,the Z→0.In addition,from the central limit theorem,we have Wn→W(Θ),a.s..

§3.The Credibility Model with Multiple Contracts
In real applications,however,the structure function π(θ)usually can not be completely speci fied so that the structure parameters are actually unknown.Therefore,the claim experiences over a number of risks in the same portfolios have to be observed in order to estimate π(θ)or the collective premium from empirical Bayes techniques.We consider a portfolio of K insured individuals,which has been studied in Wen[9].In this portfolio,each individual i is associated with a claim experience Xijover n time periods j=1,2,···,n.Write Xi=(Xi1,···,Xin)0,i=1,2,···,K.Our interest is to predict the future claim Xi,n+1for each individual,taking into account all observed claim experiences X1,X2···,XK.Formally,the assumptions of the model of multiple contracts are stated as follows.
Assumption 3.1For fixed contract i,givenare conditionally independent,withandIn addition,
Assumption 3.2The risk parameter Θ1,Θ2,···,ΘKare independent with the same structure distribution function π(θ).
Assumption 3.3The random vectors(Xi,Θi)are independent and identically distributed for i=1,2,···,K.
Our goals are to estimate the individual MLINEX premium H(X,Θi)of the i-th contracts for i=1,···,K.So we firstly consider the inhomogeneous estimators of W(Θi)by means of credibility idea,i.e.,to solve the following optimal problem

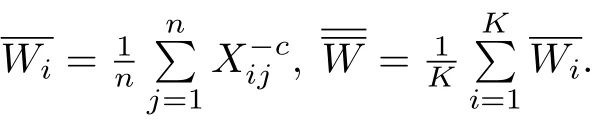
Theorem 3.1Under assumptions 3.1-3.3,the inhomogeneous credibility estimators of W(Θi)for i=1,···,K is given by

Consequently,the inhomogeneous credibility estimators H(X,Θi)under MLINEX loss function is

Remark 3.1In this model,if the nimay be di ff erent for i=1,···,K,the results of Theorem 3.1 are still true with
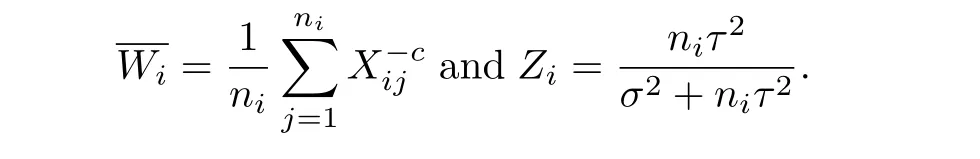

If we construct the estimator of W(Θi)to be a homogeneous linear class of samlpe,we can derive the homogeneous credibility estimator.Hence we should solve the following problem

Then we obtain the theorem as follows.
Theorem 3.2The homogeneous credibility estimators of W(Θi)for i=1,2,···,K is

where Ziis the same as in Theorem 3.1.
ProofNoting that,The optimization problem(3.4)is as the same to

Analogy to the proof of Theorem 2.2,we can get

§3. Estimation of Structure Parameters

Proposition 4.1The unbiased estimators of σ2and τ2are given by

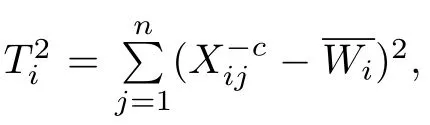



then

So

§3.Numerical Example


In this simulation,we take α =2, β =5 and c= −1.Six di ff erent values θi=0.1,0.2, ···,0.6 and three sample sizes n=10,100,500 are considered.For each combination of values of parameters θiand n,we carry out a simulation of 10000 times.The simulation results are listed in the following tables:
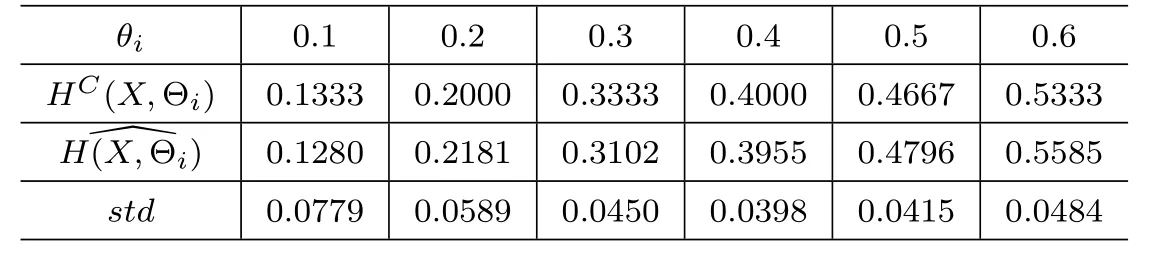
Table 1 the results with n=10
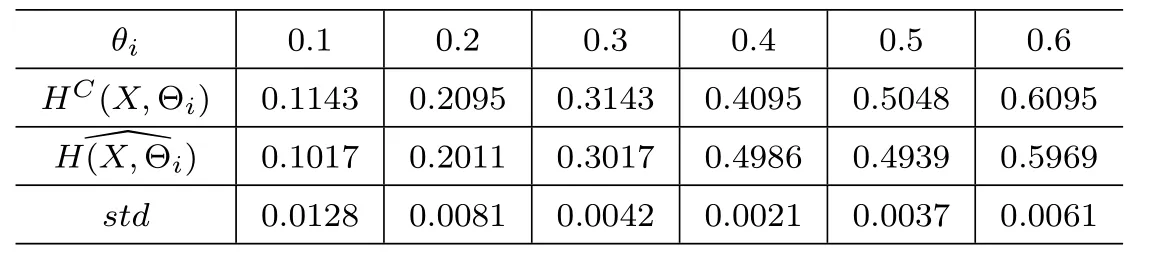
Table 2 the results with n=100

Table 3 the results with n=500
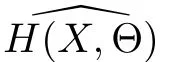
[1]BÜHLMANN H.Experience rating and credibility[J].Astin Bulletin,1967,4:199-207.
[2]BÜHLMANN H,GISLER A.A Course in Credibility Theory and its Application[M].Netherlands:Springer,2005.
[3]VARIAN H R.A Bayesian approach to real estate assessment,Studies in Bayesian Econometrics and Statistics in Honor of Leonard J Savage[J].Amsterdam:North-Holland,1975,195-208.
[4]BERGER J O.Statistical Decision Theory:Foundations,Concepts and Methods[M].New York:Academic Press,1980.
[5]FERGUDON T S.A Decision Theoretic Approach[M].New York:Academic Press,1967.
[6]ZELLNER A.Bayesian estimation and prediction using asymmetric loss functions[J].Journal of the American Statistical Association,1986,81(394):446-451.
[7]LIN Jin-guan.Parameter estimations of Rayleigh distribution[J].Chinese Quarterly Journal of Mathematics,2000,15(4):49-54.
[8]WEN Li-min,WU Xian-yi,ZHAO Xiao-bing.The credibility premiums under generalized weighted loss functions[J].Journal of Industrial and Management Optimization,2009,5(4):893-910.
[9]WEN Li-min,WANG Jiang-feng,WU Xian-yi.A new class of credibility estimators under the generalized weighted premium principle[J].Communications in Statistics-Theory and Methods,2013,42(3):447-465.
[10]KANG Hui-guang,SHI Yi-min,ZHAO Xiao-shan.Empirical Bayes Estimation for the parameter of twodimensional One-side truncated distribution families with LINEX loss[J].Chinese Quarterly Journal of Mathematics,2001,16(3):14-21.
[11]WEN Li-min,ZHANG Xian-kun,ZHENG Dan,et al.The credibility models under LINEX loss functions[J].Chinese Quarterly Journal of Mathematics,2012,27(3):397-402.
[12]PODDER C K,ROY M K,BBUIYAN K J,et al.Minimax estimation of the parameter of the Pareto distribution for quadratic and MLINEX loss functions[J].Pakistan Journal of Statistics-All Series,2004,20(1):137-149.
[13]DEY S,MAITI S S.Bayesian estimation of the parameter of Maxwell distribution under di ff erent loss functions[J].Journal of Statistical Theory and Practice,2010,4(2):279-287.
[14]RAHMAN H,ROY M K,BAIZID A R.Bayes estimation under conjugate prior for the case of power function distribution[J].American Journal of Mathematics and Statistics,2012,2(3):44-48.
[15]HEILMANN W R.Decision theoretic foundations of credibility theory[J].Insurance:Mathematics and Economics,1989,8(1):77-95.
 Chinese Quarterly Journal of Mathematics2018年1期
Chinese Quarterly Journal of Mathematics2018年1期
- Chinese Quarterly Journal of Mathematics的其它文章
- Common Fixed Point Results for Quasi-contractions Involving Altering Distance Functions in Ordered Cone Metric Spaces
- Some Generalized Normal Subgroups and p-nilpotency of Finite Groups
- The Growth Order of Solutions of Systems Complex Di ff erence Equations
- The{P,k+1}-re flexive Solution to System of Matrix Equations AX=C,XB=D
- Implicative Pseudo Valuations on Hoops
- An Elliptic Gradient Estimate for A Non-homogeneous Heat Equation on Complete Noncompact Manifolds
