复赋范线性空间上的(I,B)-近似保正交映射
孔亮
(商洛学院数学与计算机应用学院,陕西商洛 726000)
为了研究赋范空间的几何性质,各种正交性和近似正交性定义被相继引入和研究[1-4],其中B-正交即Birkhoff正交受到了许多学者的关注[5-8]。在此基础上,一些学者研究保持各种正交性和近似正交性映射的性质。文献[9-12]在内积空间给出了近似保正交映射的性质,文献[13-14]在实赋范空间中给出了近似保等腰正交线性映射的刻画,文献[15-17]在实赋范空间中分别研究了保ρ-正交、保ρ*-正交和近似保等分线正交线性映射,文献[18]在实赋范线性空间中引入了(I,ρ)-近似保正交映射的概念并证明了非零(I,ρ)-近似保正交线性映射有界并且是下有界的。本文在复赋范线性空间中,给出近似(I,B)-保正交映射的定义,证明非零(I,B)-近似保正交线性映射有界并且是下有界的,证明在一定条件下,非零(I,B)-近似保正交线性映射是近似保B-正交线性映射。
1 预备知识
定义1[5]若则称x和y是B-正交的,记为
定义2[7]设则称x和y是近似B-正交的,记为
定义3[7]设若则称x和y是δ-近似B-正交的,记为
定义4设映射若对任意的则称 T 是近似保B-正交的。
定义5[13]若且则称x和y是等腰正交的,记为x⊥Iy。
定义6[16]设x,y∈X,称为范数导数。
定义7设映射T:X→Y,ε∈[0,1),若对任意的则称 T 是(I,B)-近似保正交的。
2 结论及其证明
为了完成定理的证明,先介绍几个引理。
引理1设x,y∈X,则
证明由定义5可知结论成立。
引理2[8]设 ε∈[0,1),x,y∈X,则
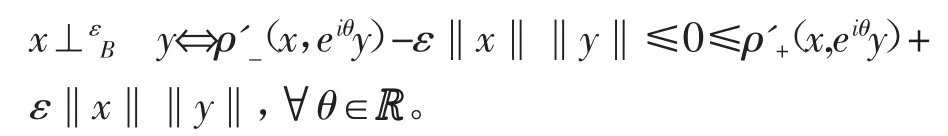
引理3[8]设定义映射为为 φ(t)=‖u+tv‖2+a‖u‖‖tv‖。 若φ(0)<φ(t),∀t∈[b1,b2]{0},其中b1<0,b2>0,则φ(0)≤φ(t),
定理 1设 ε∈[0,2-1),T:X→Y 是非零(I,B)-近似保正交线性映射,则T有界且‖T(x)‖,∀x∈X。 从而 T 是下有界的。
证明设x,y∈X且‖x‖=‖y‖=1, 则由引理1知于是由(I,B)-近似保正交线性映射的定义知从而由引理2得有

和

于是对任意的γ∈(0,1),

由T是线性映射和范数导数的定义可知
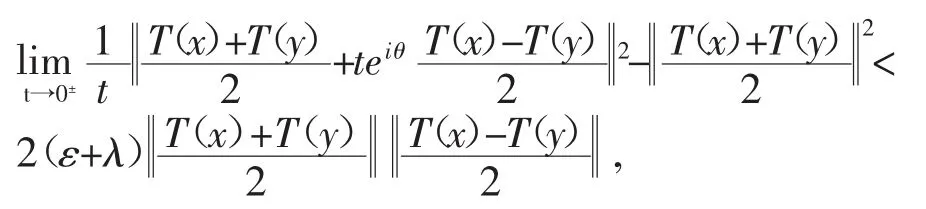
由极限的保号性得,存在 δ1<0,使得∀t∈[δ1,0),

同理由(2)式和极限的保号性得,存在 δ2<0,使得∀t∈(0,δ2],(3)式成立,故∀t∈[δ1,0)∪(0,δ2],(3)式成立。定义凸函数


在(4)式中令γ→0得

在(5)式中令 θ=0,t=1 得

则由文献[18]定理1的证明知T有界且
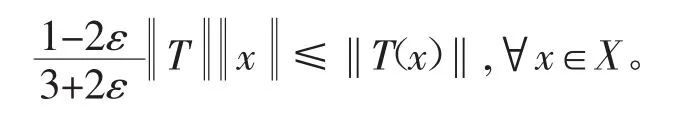
定理 2设 ε∈[0,2-1),T:X→Y 是非零(I,B)-近似保正交线性映射,则T:X→Y是近似保B-正交映射。
证明由定理1知

设 x,y∈X 且 x⊥By,即于是有


