一类分数阶广义捕食者-食饵模型的动力学分析
蒲武军,杜争光
(陇南师范高等专科学校数学系,甘肃陇南 742500)
分数阶微积分将导数和积分推广至任意阶,分数阶微分方程常被用来描述黏弹性、电动电路、电化学现象等.近年来,随着分数阶微积分方程研究的不断发展,分数阶种群系统的动力学研究逐渐成为了一个热点课题,并且已经取得了一系列好的结果[1-4].Erbach等[5]讨论了一类广义捕食系统的双稳态和极限环的存在性问题,指出广义捕食系统的动力学行为较具有一般反应函数的捕食系统更加丰富.El-Shahed[6]等讨论了一类分数阶广义捕食者-食饵模型正平衡点的存在性、稳定性和极限环.目前,针对Holling-Ⅱ型功能反应的分数阶捕食系统的研究已有许多结果[7-9].
文中考虑一类具有Holling-Ⅱ型功能反应的分数阶广义捕食者-食饵模型:
(1)
其中α∈(0,1],r,K,β,δ,σ,c,d,e均为正常数,x,y分别表示食饵和捕食者的种群密度,初始条件为x(0)>0,y(0)>0且c>e.有关系统(1)的详细生物学意义参见文献[5].
1 预备知识和引理
首先介绍分数阶微积分的相关知识.

其中Γ(·)是伽玛函数.
定义2[11]Caputo分数阶导数定义如下:
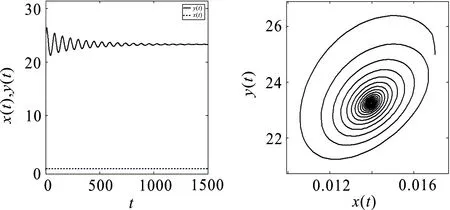
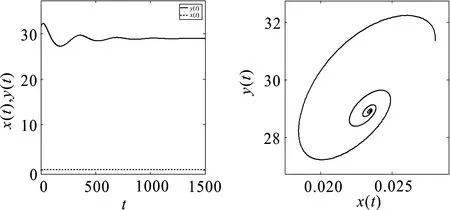
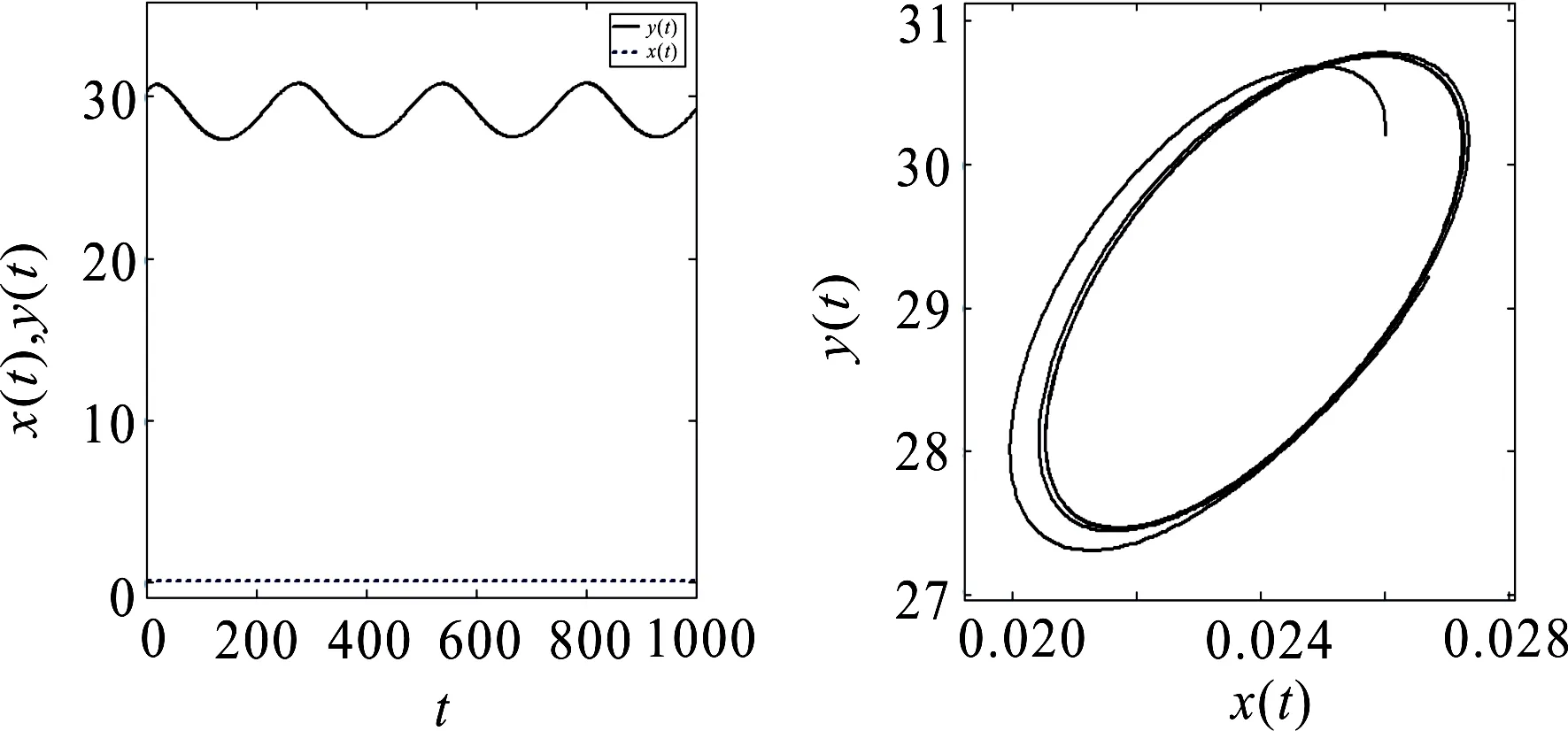
其中α>0,n-1<α 设分数阶系统 (2) 有平衡点(xe,ye). 引理1[12]分数阶系统(2)的平衡点(xe,ye)是局部渐近稳定的当且仅当雅克比矩阵 引理2[13]设x(t)∈R+是一个连续可微函数,则对任意时刻t≥t0,有 引理3[14]考虑如下分数阶系统: Dαx(t)=f(t,x),t>t0, (3) 引理4[14](比较定理) 若Dαx(t)≤Dαy(t),x(0)=y(0),其中α∈(0,1],则x(t)≤y(t). 引理5[15]设u(t)是定义在[t0,∞)上的连续函数且满足 其中0<α<1,(λ,μ)∈R2且λ≠0,初始时刻t0≥0.则 其中Eα是M-L函数,即 定理1对任意初值(x(t0),y(t0))∈Ω,Ω={(x,y)∈R2:max{|x|,|y|}≤M},系统(1)存在唯一解X=(x,y)∈Ω. (4) 其中 即系统(1)关于X满足局部利普希茨条件,由引理3知系统(1)存在唯一解. 】 定理2记Ω+={(x,y)∈Ω:x∈R+,y∈R+},且x(t0)>0,y(t0)>0.则对任意始于Ω+的初值,系统(1)的所有解是非负的. 定理3集合 是关于系统(1)的正不变集,且对任意初值条件(x(t0),y(t0))∈Ω+,Γ是关于系统(1)的全局吸引集,并且系统(1)的所有解均有界. 由引理5可得 因此,系统(1)始于Ω+的所有解均位于集合 中,即Γ是关于系统(1)的正不变集. (7) 其中, 显然,系统(1)的平凡平衡点E0(0,0)和边界平衡点E1(K,0)均不稳定. 定理4若red<β(c-e),则系统(1)的边界平衡点E2局部渐近稳定;若red>β(c-e),则系统(1)的边界平衡点E2不稳定. ( i )tr(J(x*,y*))≤0; ( ii )tr(J(x*,y*))>0, 则系统(1)的正平衡点E3(x*,y*)局部渐近稳定. 证明由(7) 式得系统(1)在正平衡点E3(x*,y*)的雅克比矩阵为 其特征方程为 λ2-tr(J(x*,y*))+det(J(x*,y*))=0, 故其特征根可表示为 若条件( i )成立,则有下列3种情形: 在初中数学教学实践过程中,培养学生自身的创新思维有着非常重要的教学意义。随着新课改的贯彻落实,培养创新思维已经逐渐成为初中数学教学过程中非常关键的内容,教师在教学期间不仅要高度重视数学知识的科学传授,还必须要强调学生的创新思维能力的锻炼与培养,从而使每位初中生都可以运用创新思维有效解决数学问题,养成良好的数学学习习惯,增强学生的创新意识,为未来学习奠定良好的基础。 综上可知,在条件( i )下正平衡点E3(x*,y*)局部渐近稳定. 若条件( ii )成立,则由特征值表达式(8)和(9)可知:λ1和λ2是一对共轭复根,且 于是 这意味着 故 由引理1可知,在条件( ii )下正平衡点E3(x*,y*)局部渐近稳定. 】 定理6若eσ<δ,β(c-e) ( i )tr2(J(x*,y*))-4det(J(x*,y*))≥0; ( ii )tr2(J(x*,y*))-4det(J(x*,y*))<0, 则系统(1)的正平衡点E3(x*,y*)不稳定. 证明若条件( i )成立,则其特征方程至少有一个正根,此即意味着平衡点E3(x*,y*)不稳定. 若条件( ii )成立,则λ1和λ2是一对共轭复根,且 结合条件(2),有 即 故 结合引理1知平衡点E3(x*,y*)不稳定. 】 证明定义E3(x*,y*)处的Lyapunov函数V(t)为 其中L>0,则由引理2可得 即得 例1取r=0.6,K=1,σ=40,β=0.04,δ=20,c=0.5,d=1,d=0.48,α=0.99.显然不等式eσ<δ,β(c-e) 图1 平衡点E3(0.5146,157.15)局部渐近稳定 图2 平衡点E3(0.0139848,23.2273)局部渐近稳定 (a)α=0.53 (b)α=0.58 (c)α=0.612 若取K=2,e=0.2,α=0.71,其他参数不变,则不等式eσ<δ和β(c-e) 取K=2,δ=15,其他参数不变,α分别取0.53,0.58和0.612,两不等式仍然成立,图3(a)~(c)体现了相应的平衡点从稳定到不稳定的变化过程.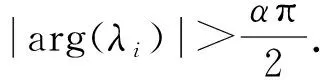

2 主要结果及其证明
2.1 解的存在唯一性
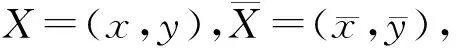

2.2 非负性和有界性
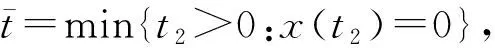

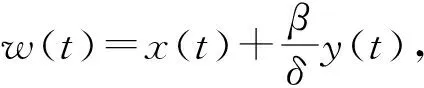
2.3 平衡点的局部稳定性


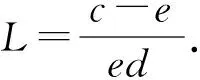

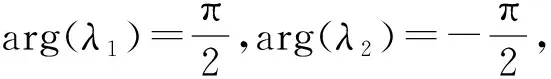
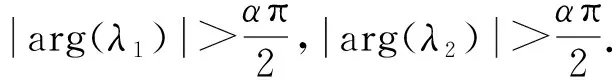
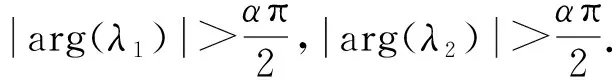
2.4 平衡点的全局渐近稳定性
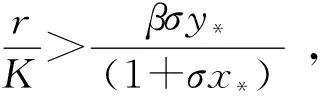

3 数值模拟