外来物种入侵的Logistic时滞模型的稳定性与Hopf分支分析

张巧玲，陆海霞,张 翼

(1.宿迁学院 文理学院，江苏 宿迁 223800；2.沈阳工业大学 理学院，辽宁 沈阳 110870)

0 引言

种群生态学是生态学中发展最为成熟的一个重要分支.对于生态学中的一些有趣现象，我们可以用数学理论解释说明，而生态现象又是检验数学理论的最好实践，两者之间相互联系、彼此促进，使得两门学科共同发展.近年来，种群生态学研究备受关注[1-4].随着经济的不断发展，人们对生态环境的保护更加重视，对生物种群的数学研究也越来越细化[5-10].

文中是关于水生植物大米草的研究.近些年来,随着我国水产养殖业的迅猛发展以及资源增殖放流的需要,从国外引进水生物种步伐加快,水生外来物种安全状况也令人担忧[11].因此，对外来物种的研究也越来越多[12-15].文中综合运用微分动力系统的分支理论和外来物种入侵规律，以养殖渔业为背景，通过数学建模分析生态系统的平衡点及其稳定性.分别以养殖对象和外来物种为研究对象，引入净化努力量，不仅能够更好地揭示生物发展规律，而且有利于促进经济发展和环境保护.

本文的创新之处在于将外来物种与时滞模型结合.大米草的净化努力量对物种密度的影响具有延迟效应，并且鱼类种群的孕期时滞也会使种群密度发生改变，所以考虑孕期时滞和净化时滞，可以提高系统描述的真实性.大米草可以促淤围垦、改善土壤，改善土壤性质才能起到保护环境的作用,因此控制大米草的密度是非常重要的.实际上，由于考虑时滞影响，系统会存在一些很复杂的动态特性，如Hopf分支，它们会影响系统的稳定性.特别地，本文模型展示了时滞τ=0和τ≠0时系统的平衡点及其稳定性.根据Hopf分支理论，分析正平衡点出现Hopf分支的临界时滞τ0；对τ<τ0及τ≥τ0分别进行仿真分析，从生物学角度揭示时滞对整个生态系统的重要意义.

1 系统建模

生态学上著名的Logistic方程为

其中，N(t)为t时刻的种群数量或密度，r为该种群的内禀增长率，即出生率减去死亡率，K为环境容纳量.文献[12]研究了外来物种入侵下单种鱼群Logistic增长模型的分岔及控制,考虑如下带有捕获努力E(t)的增长模型：

(1)

在该模型中，x(t)为t时刻鱼群的密度，y(t)为t时刻外来物种大米草的密度，E1(t)为渔民对大米草的净化努力量，β为大米草的内禀增长率，-hE1(t)为人为净化大米草的量，θy(t)为大米草的疯长程度，ω为单位净化行为的成本，-αx(t)为鱼群数量减少刺激的净化努力.

引入时滞τ1,τ2，考虑如下模型：

(2)

(3)

文中研究系统(3)在时滞τ=0和τ≠0时的动力学行为，分析系统出现Hopf分支的临界时滞，并通过仿真验证理论分析结果.最后，从生物学角度讨论时滞制定对于生物保护和治理外来物种的实践意义.

2 无时滞时平衡点的稳定性分析

引理1若系统(3)中参数均为正常数，且满足M>hθ+βω+Knαβω，令P(t)=(x(t),y(t),E1(t))表示系统(3)的平衡点.则对所有t≥0，系统(3)的平衡点被定义在[0,+∞)上，且存在正平衡点.

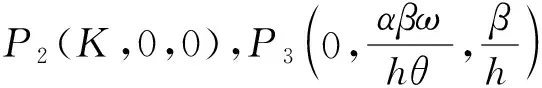
这里

当M>hθ+βω+Knαβω时，正平衡点P*=(x*,y*,E*1)存在.

为了简便，以下记τ1=τ2=τ.本节主要讨论τ=0时，系统各平衡点的稳定性.

定理1平衡点P1(0,0,0)是不稳定的鞍结点.

证明将系统(3)在平衡点P1(0,0,0)处线性化可得

由此得到的特征方程为

(λ-r)(λ-β+he-λτ)(λ+ω)=0，

当τ=0时对应的特征值:λ1=r>0,λ2=β-h,λ3=-ω.故P1(0,0,0)不稳定. 】

定理2如果β-h<0,则平衡点P2(K,0,0)是稳定的.

证明将系统(3)在平衡点P2(K,0,0)处线性化可得

由此得到的特征方程为

(λ+r)(λ-β+he-λτ)(λ+ω)=0，

当τ=0时，对应的特征值:λ1=-r<0,λ2=β-h<0,λ3=-ω<0.故P2(K,0,0)是稳定的. 】

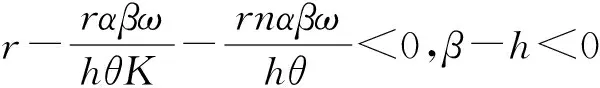
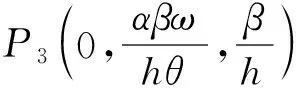
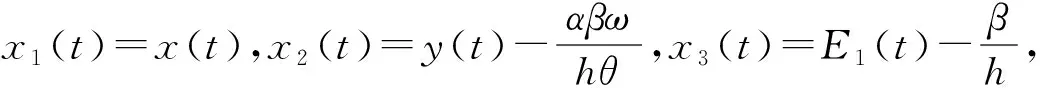
该点处的线性化系统为

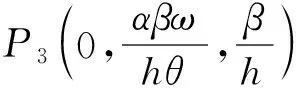
定理4系统(3)的正平衡点P*=(x*,y*,E*1)渐近稳定当且仅当以下条件同时成立：

( i )A1+B1>0;

( ii )(A1+B1)(A2+B2)-(A3+B3)>0;

(iii)A3+B3>0.

其中

证明系统(3)在正平衡点P*=(x*,y*,E*1)处的Jacobi矩阵为

其中，

从而系统(3)在正平衡点处的特征方程为

若τ=0，则特征方程变成

λ3+(A1+B1)λ2+(A2+B2)λ+(A3+B3)=0.

利用Hurwitz判据[16]，特征方程的特征根全部都具有负实部的充分条件是：

即

故τ=0时，系统(3)的正平衡点P*=(x*,y*,E*1)渐近稳定当且仅当条件(i)～(iii)成立. 】

3 时滞影响下的稳定性与Hopf分支分析

定理5τ>0时，若Q1>0,Q2>0,Q3>0，则存在τ=τn，n∈N，使得

( i )当τ在τ0附近且τ∈[0,τ0)时，系统(3)的正平衡点局部渐近稳定；

( ii )当τ=τn,n∈N时，系统(3)在正平衡点附近出现Hopf分支.

其中

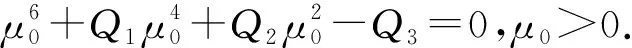
证明(i) 设λ=iu(u≠0)为特征方程(4)的一个纯虚根，代入(4)式得到

分离实部和虚部，有

(5)

其等价于(A1μ2-A3)2+(μ3-A2μ)2=(B2μ)2+(B1μ2-B3)2,即

为方便讨论，不妨设

将μ0代入方程组(5)，可得

从而得到与μ0相对应的临界时滞τ，记作τn，即

根据Hopf分支理论[17]可知，当τ∈[0,τ0)时，特征方程(4)的根都具有负实部,即当τ在τ0附近且τ∈[0,τ0)时，系统(3)的正平衡点局部渐近稳定.

( ii )设λ=λ(τ)=Re(λ(τ))+iIm(λ(τ))为特征方程(4)的一个复根(满足λ(τn)=iμ0≠0)，将其代入(4)式，不难得到

又

从而

已知条件Q1>0,Q2>0，所以

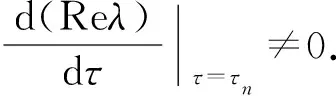
4 仿真

使用文献[12]中的仿真数据，取r=1,K=4,n=0.1,β=3,h=2.5,θ=1,ω=0.45,α=0.5,τ1=τ2=0.1，则系统(3)变为

正平衡点P*=(x*,y*,E*1)=(1.826,1.2526,1.2)，此时τ0=0.6807.由定理5可知:

( i )当τ在0.6807附近且τ∈[0,0.6807)时，系统(3)的正平衡点局部渐近稳定；

( ii )当τ=0.6807，n∈N时，系统(3)在正平衡点附近出现Hopf分支.

图1说明取初始值(0.1,0.1,0.1)，当τ=0.1<τ0时系统(3)的正平衡点P*=(x*,y*,E*1)是渐近稳定的.图2说明取初始值(0.1,0.1,0.1)，当τ=0.6807=τ0时系统(3)的正平衡点P*=(x*,y*,E*1)是不稳定的并且存在稳定的周期轨迹.极限环在参数τ大于分岔值τ0的范围内存在，因此为超临界Hopf分岔，并且分岔周期解在轨迹上渐近稳定.

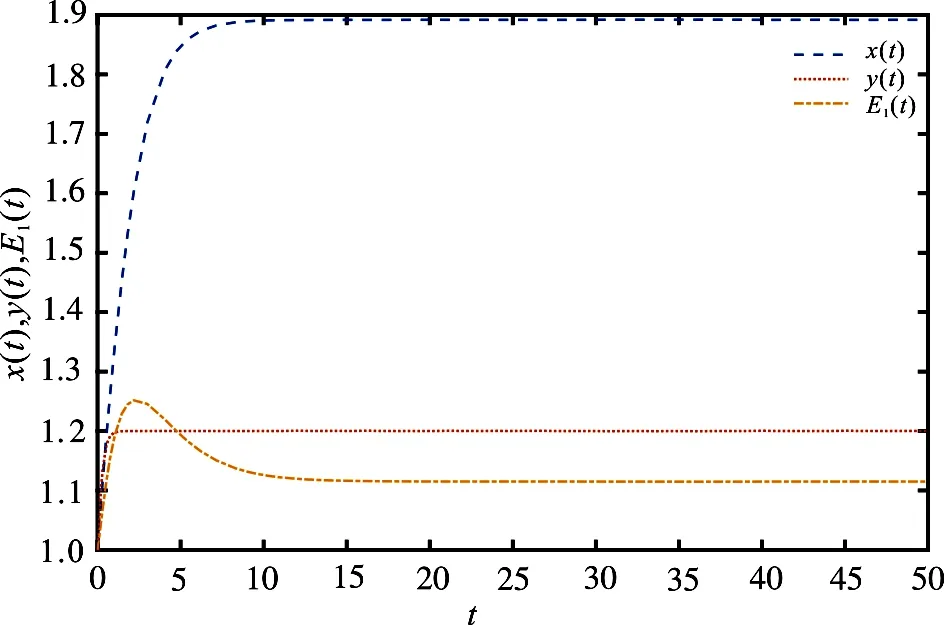
图1 当τ=0.1<τ0时x(t),y(t),E1(t)的状态响应

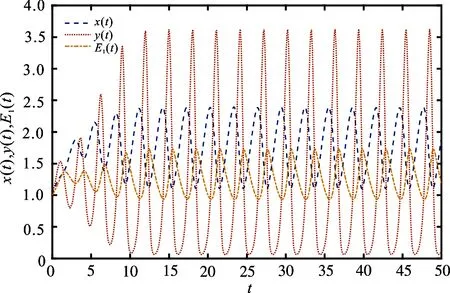
图2 当τ=0.6807时x(t),y(t),E1(t)的状态响应

5 结束语

文中以大米草为例，运用微分方程定性理论，研究了具有净化努力量和时滞的Logistic模型的动力学行为.通过建模分析，得到以下结论：当τ=0时，零平衡点是不稳定的鞍结点，系数满足一定条件时，两个边界平衡点和正平衡点是稳定的；当τ≠0时，存在临界时滞τ0，当τ在τ0附近且τ∈[0,τ0)时，系统(3)的正平衡点局部渐近稳定；当τ=τn,n∈N时，系统(3)在正平衡点附近出现Hopf分支.从仿真结果可见，在一定范围内缩短时滞有利于系统稳定性的提高.在实践中，提高净化努力量的效率,如发放净化补贴、选育产程较短的鱼苗等政策和手段，都有利于保持渔业生物系统的稳定性.这对于维持生态系统的持续良好循环、改善水陆环境以及长期稳定地获取经济利益具有积极而又深远的影响.