自旋轨道耦合自旋1旋量玻色-爱因斯坦凝聚体中波的传播

薛具奎，万年胜

(西北师范大学 物理与电子工程学院，甘肃 兰州 730070)

玻色-爱因斯坦凝聚体(BEC)[1-3]中线性与非线性波研究一直是人们关注的热点问题.随着科技发展与认识水平的进一步提高，标量和旋量玻色系统中波的传播特性得到了详细的研究，取得了丰硕的成果[4-8].最近，美国国家标准与技术研究所完成了一项具有里程碑意义的实验，在87Rb原子的BEC中实现和观测到了自旋轨道耦合现象[9].这一突破性的进展又为此领域的研究打开了一扇新的大门.

一般来说，没有自旋轨道耦合时，玻色系统表现出各种各样的磁现象，通过一个外部的塞曼场可以调控系统的磁化，从而观测研究系统各类基态.自旋轨道耦合的实现不仅带来了许多可调的参数，还因其典型的非线性特性带来更多更有趣的奇异基态，如平面波相[10]、驻波相[11]、三角晶格相[12]以及方格相[13].特别是自旋轨道耦合引起的非线性激发更是成为了人们研究的焦点.许多新奇的拓扑相干结构已经成功找到并得到了详细的研究.例如，斯格明子[14]、涡旋[15]、狄拉克单极[16]等，尤以孤子形式的非线性激发受到物理学家的青睐[17-20].大量的相干结构被发现，例如暗-亮孤子复合体[21]、磁畴壁[22]、反涡旋偶极子[23]等.人们首先在两组份BEC 中研究了自旋轨道耦合对孤子传播特性的影响[24]，不久又在不同维度的自旋轨道耦合BEC 中展示了孤子的传播特性[25].有趣的是，具有自旋轨道耦合的两组份BEC 因其特有的激发能谱还存在正负质量孤子.最近的研究又表明，自旋轨道耦合对自旋1旋量BEC的基态结构[26]、相分离[27]、元激发[28]及量子相变[29]等各个方面都有十分重要的影响.然而关于该系统中孤立子波的研究由于其复杂性仍处于探索阶段.

自旋轨道耦合效应如此丰富的非线性特性对波传播的影响必将非常显著.因此，文中重点讨论了具有自旋轨道耦合的自旋1旋量BEC系统中线性与非线性波的传播特性.由描述该系统的三组份GP方程出发，首先考虑在弱扰动情形下的线性波激发，解析地得到了平面波解及其存在的条件.其次，以平面波解分析为基础，研究了强扰动情形下的非线性波激发，即文中的孤子解.

1 模型

考虑自旋轨道耦合自旋1旋量BEC囚禁于准一维势阱中，此时囚禁势沿着y轴和z轴方向的频率要远远大于沿着x轴方向的频率，即ωy,ωz≫ωx[27].其次，考虑具有相同强度的Rashba和Dresselhaus型自旋轨道耦合，则系统单粒子哈密顿量可写为[29]

(1)

(2)

在平均场理论下，使用单粒子哈密顿量表达(1)式，并考虑Hartree 近似，则自旋轨道耦合自旋1旋量BEC 可被如下一组耦合GP方程描述

方程(3)～(5)式可被如下条件进行无量纲化处理:

(8)

得到无量纲GP方程

值得注意的是，不考虑自旋轨道耦合时，也就是γ=0时，方程(9)～(11)在两种特殊的参数条件下是可积的，这意味着可以写出其具体形式的解.第一种情况是c2=0，这时方程(9)～(11)是一组非线性薛定谔方程.第二种情况是c2=c0，此时方程(9)～(11)是一组可积的矩阵非线性薛定谔方程[4].而根据不同的参数关系，系统可能有亮孤子解、暗孤子解、亮-暗孤子解以及畴壁解[30].

当外部囚禁势非常弱的时候，可以将外部势V(x)忽略，因此文中仅考虑均匀情况下系统的线性与非线性波解.此时系统的总能量可写为

基于上述能量函数的形式，很容易推导出系统各组份之间的相分离.

2 平面波解

下面讨论系统在弱扰动下的线性激发，由于三组份GP方程是一组不可积的偏微分方程，它没有一个通解，因此以平面波解作为初始波函数进行分析讨论，假定其具有如下形式

其中,kj为波数；Ωj为频率；θj为相位；Aj为振幅且取为正实数.

将波函数(16)代入方程(9)～(11)，并考虑到波数、频率都是实数，因此三组份参数应满足

这里n是任意整数，表示不同模式的平面波解，其具体的取值主要取决于系统的基态性质，用来调控系统处于能量最低的态上，下文中用n=0和n=1分别代表n取偶数和奇数.使用上述参数条件得到

需要注意的是方程(18)应该是一致的，由相容性条件出发得到

(19)

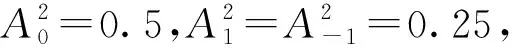
将(19)式代入(18)式简化得到系统的色散关系

(20)

特别需要强调的是，平面波的频率是表征系统色散情况的重要物理量之一，充分反映了系统的基态性质.这里频率Ω由原子间相互作用、波数、自旋轨道耦合、参数n以及0组份原子数密度共同决定.有趣的是，不同参数下系统具有不同的色散行为，可以通过调控参数，研究系统的基态性质.图1-2给出了不同参数下系统的色散关系，其中碰撞相互作用c0=2,A0=0.5.图1a～c展示的是n取偶数时频率Ω随原子自旋交换相互作用c2的变化趋势.可以清晰的看到，无论是在铁磁还是反铁磁凝聚体中，不考虑自旋轨道耦合时，Ω是关于k对称的，并且在k=0处取最小值对应凝聚体的基态.当我们进一步考虑自旋轨道耦合相互作用时，Ω取最小值时所对应的k值发生了明显的偏移，并由(20)式可知，此处k=-γ.图1d～f展示的是n取奇数时频率Ω随原子自旋交换相互作用c2的变化趋势.显然，不考虑自旋轨道耦合时的情况与n取偶数时一致，当引入自旋轨道耦合后，此时Ω在k=γ处取得最小值对应凝聚体的基态.由上述讨论得出平面波与n取奇数或偶数的关系，即k>0时，

图1 频率Ω随原子自旋交换相互作用c2的变化规律

n取奇数；k<0时，n取偶数.

此外，随着自旋交换相互作用c2的增加，频率Ω呈现增大的趋势，也就是说铁磁凝聚体的基态能量要高于反铁磁凝聚体的基态能量.图2展示的是频率随波数的变化趋势.可以清晰的看到，色散关系表现为抛物型结构，不考虑自旋轨道耦合的情况下在k=0处频率Ω取得最小值，引入自旋轨道耦合后，n取奇数时频率Ω在k=γ处取得最小值，n取偶数时频率Ω在k=-γ处取得最小值，结果与图1分析一致.

综上所述，自旋轨道耦合显著地改变系统色散关系，从而改变凝聚体基态及平面波的性质.

图2 频率Ω随波数k的变化规律

3 孤子解

首先假定孤子具有如下形式:

将(29)式代入方程(9)～(11)得到

对于这样一个复杂的三组份偏微分方程而言，要得到它的孤子解是困难的，而对于单组份的非线性薛定谔方程来说，它的孤子解却是为人们所熟知的，因此通过一些运算使三组份的偏微分方程简化为一个单组份的非线性薛定谔方程，进而得到系统的孤子解.为了达到这样的目的，采用上一部分中类似的解法，并使用(19)式，则方程(30)简化为

然后利用变换Ψ=φexp(iγx+iγ2x/2)消除方程(31)中的最后一项得到非线性薛定谔方程

至此达到了将三组份的偏微分方程简化为单组份非线性薛定谔方程的目的，对于这样一个熟知的非线性薛定谔方程来说，当c0+c2>0时可得到系统的暗孤子解

图3 亮孤子随波数k的变化规律

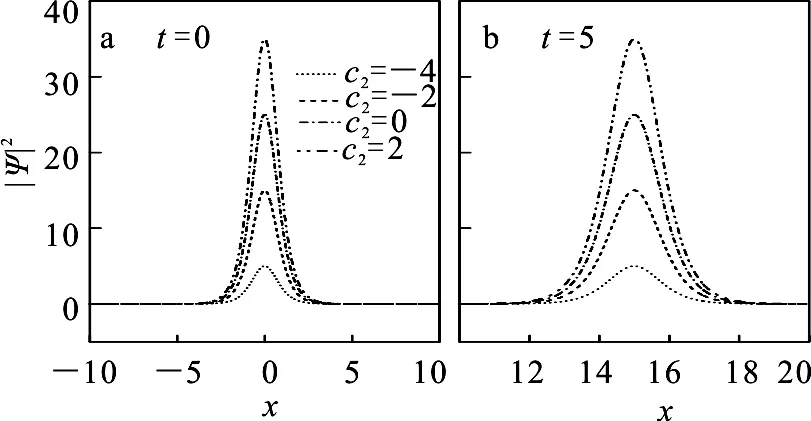
图4 亮孤子随自旋交换相互作用c2的变化规律

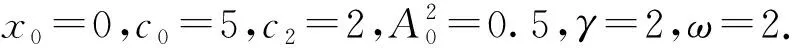
4 结束语

研究了自旋轨道耦合自旋1旋量玻色-爱因斯坦凝聚体中线性与非线性波的传播特性.在平均场理论下，自旋轨道耦合自旋1旋量玻色-爱因斯坦凝聚体可被三组份GP方程描述.研究了弱扰动下系统激发的线性波解，获得了系统的平面波解及其存在条件，并讨论了自旋轨道耦合对系统基态性质的影响，同时给出了两种模式的平面波参数n的取值依据.其次，考虑了强扰动下系统激发的非线性孤子解.由于三组份GP方程是不可积的复杂偏微分方程，因此将其简化为一个等效的非线性薛定谔方程.通过这个非线性薛定谔方程，分析研究了系统的亮孤子解和暗孤子解，并给出了各参数对孤子振幅和宽度的影响趋势，发现随着原子间相互作用或波数的增加，孤子的振幅呈现增大的趋势，而孤子的宽度呈现变窄的趋势.