例谈创造性思维的自我培养
(湖南省长沙市周南梅溪湖中学 湖南长沙 410002)
创造性思维是个体不依照常规思考问题,寻求变异,建立新的理论,用新的思维、方可来解决问题的方式。[1]
在教学中,创新从来都是一个常谈、常讲、又常很困难的一件事情。老师在教学中难以把握,难以传授。或者说老师自己本身就很难办到,要求学生能够做到就可想而知了。下面以从举例法出发,针对创造性数学思维的自我培养方式进行探讨和分析。
一、培养发散思维——从多方面多角度去思考问题
例如数形结合,立几和向量结合,三角和函数结合,解几和向量结合,数列和函数从而和图形结合等等,都适合采用这种方式。
在传统的数学教学活动中,一般是根据既定的内容、标准来传授知识结构,从单向思维的角度来联系内容学习公式、定理,这种思维模式是单一的,知识解决问题的基本方式。但是,如果一直按照这种模式来解决问题,必然会出现思维定势,影响创造性思维能力的发展。[2]
尤其是在学期结束时期上复习课,老师可以把整个内容从整体上划分为几个大的部分,例如我在期末复习中,会将整个立体几何和空间向量、棱柱和棱锥、球及欧拉公式从整体上联系结合,将内容分成三个部分,即线线关系、线面关系、面面关系,学生在复习当中,普遍反映一下子要用到好多好多的知识,涉及高一、高三的内容;在对高三的高考内容的复习当中,我是结合导数和函数,导数和图形,导数和不等式来复习的,达到很理想的效果,学生在无形中,可以将整个高中内容百分之80到百分之90的内容又过了一遍,好像不仅局限于高二的复习内容,突然觉得可以用很多方法来解决问题了。[3]
为此,在数学学习中,要掌握发散性思维的应用方式,掌握一题多解、一题多变等方法的应用,我们来看一个例题,举例来说明发散思维该如何考虑。
根据题目的特点,可以从不等式、数列、函数、几何、三角等内容来分析和思考,通过对比来找出最合适的解决方式,根据种种分析可以得出:
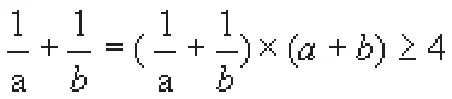
解决上述问题的最有效方式。除了该种方式之外,还可以改变题设、结论、条件来进行训练。根据本题,可以采用如下的拓展方式:

通过一系列的训练,可以从多个角度分析问题,加深自身对于知识的感受和理解,提高解题能力和思维能力。
二、善用逆向思维——“正难则反”的数学思维
如果采用从正面入手很难找到突破口,我们则会思考反面入手,即我们常说的逆向思维。常见方法以反证法最为突出。逆向思维最大的好处在于培养自己独立的思考能力,锻炼自己的头脑。碰到较难找到方法的题目,请你常试着倒过来想一想。
正向思维就是以已知条件为出发点,按照常规的解题思路、先后顺序来解决数学问题,所谓逆向思维,就是正向思维的相反,在解题时,应用逆向思维,能够锻炼独立思考能力,突破学习中的难点和重点,将难题简单化。
如,数 y=f(x)的图象上的每一点的纵坐标不变,将横坐标伸长至2倍,把图象沿X轴向左边平移个单位,再沿Y轴向下平移1个单位,得出的图象和图象相同,那么f(x)的表达式是?
在这一题目中,如果按照常规的思维来分析,解答过程十分繁琐,为了简化解题方式,可以尝试采用逆向思维,让解题过程变得简单明了。
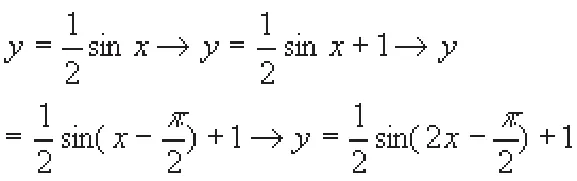
三、构建整体思维——整体思维是整体原理在数学中的反映
在解决数学难题的过程中,思维不一定集中在个别问题上,有的时候,将问题看做一个整体,往往可以取得意想不到的效果,对问题的整体结构、形式进行处理,即可简单、顺利的解决问题,即要学会站在一定的高度来看问题,先宏观调控,在各个点来击破。
例如,求sinl0°.sin30°.sin50°.sin70°的值.
在解决这一问题时,可以乘积看成整体,可得如下解法:设a=sinl0°.sin30°.sin50°.sin70°,b=cosl0°.cos30°.cos50°.cos70°两式相乘然后运用倍角公式后可解得。
此外,还可以把a直接转化为cos80°.cos60°.cos40°.cos20,通过这种转化方式,让解题过程变得更加简单,老师在教学的时候可以以此来推广,多让学生总结。
再以某高考题为例:
四、注意直觉思维
在解决数学问题时,可以先对解题途径、结果进行大概的猜测,得出大致的解题方向,这就是直觉思维,在解决数学问题时,不能忽视直觉的出现,这种直觉,往往是你在不经意中对这道题的一个宏观把握,难怪有人说,在考试的时候,我突然灵光一现,会达到意想不到的结果。对于抽象的数学问题,都可以采用直觉思维来解决问题,将抽象思维转化为形象思维,得出正确的答案。
思维是解决数学问题的基础,也是重中之重,思维的核心,便是其创造性、独立性,要解决数学问题,不仅要把握好定理、公式的应用,还要掌握思维方式的应用,以此来提高自身的素质,成为综合能力过硬的人才。

