半线性椭圆方程组正解的存在性
张亚静,杨燕君,郭伟香
(山西大学 数学科学学院,山西 太原 030006)
0 引言
本文研究以下半线性椭圆方程组
(1)
(2)

(3)
其中βjj>0,j=1,2,…,k,βij=βji≤0,i≠j,i,j=1,2,…,k.作者使用Pohozaev等式且通过积分估计证明了方程组(3)有无穷多个变号解。除此之外,Chen等人在文献[4]中研究了以下问题
(4)
其中λ1,λ2,μ1,μ2>0,他们证明了对任意的k∈N,存在βk>0,使得方程组对每个给定的β∈(0,βk),方程组(4)至少有k个变号解。随着研究的不断深入,许多学者都考虑了Ω=RN的情形,比如文献[5]中研究了以下问题
(5)
他们通过对f,g进行适当的假设证明了方程组(5)至少存在一个正解。在文献[6]中Liu对类似的方程组
(6)
进行了讨论,作者通过对a(x),b(x)进行适当的衰减假设,再运用临界点理论,在有界球内找到了近似解,然后通过分析找到近似解的结构再取极限,从而证明了方程组(6)有无穷多的正能量解。除此之外,Chen等人在文献[7]中研究了以下问题
(7)
作者通过对a(x),b(x)作适当的假设,证明了方程组(7)有一个正解且这个解满足一些性质。Qin等人在文献[8]中研究了以下问题
(8)
通过对a(x)和F的一些假设证明了方程组(8)有一个非负的基态解且这个解关于某个点是径向对称的。
令α=β,u=v,h1=h2=h,则方程组(1)就转化成了半线性椭圆方程
(9)
解的存在性问题,此问题在文献[9]中已经有所研究,得到方程(9)有两个正解。对于椭圆方程问题[10-12]也受到了大量学者的关注。比如在文献[10]中,Bahri研究了有界区域上的椭圆方程
(10)
作者证明了存在pN>1,使得对任意的p∈(1,pN),方程(10)有无穷多不同的解。
基于以上相关文献([1-10])的启发,本文使用集中紧性原理和山路定理研究带有扰动项的方程组(1)的正解的存在性。本文将方程(9)的结果进一步推广到对应的方程组上进行研究,我们通过集中紧性原理[13-14]来解决紧性缺失的问题。除此之外,对扰动项进行适当假设,从而获得了方程组(1)正解的存在性。
问题(1)是在Sobolev空间Ε=H1(RN)×H1(RN)的框架下提出来的,范数定义为
我们定义u+(x)=max(u(x),0),u-(x)=-min(u(x),0).
本文的结论如下:

则方程组(1)至少存在两个正解。
1 预备知识
我们定义与方程组(11)相关的能量泛函为
众所周知,泛函I的临界点是方程组(1)的正解。当p=α+β时,令
其中ω是方程-Δω+ω=|ω|p-1ω,x∈RΝ(2 (11) 易知方程组(11)有唯一解。我们定义与方程组(11)相关的能量泛函为 其中(ui,vi)(1≤i≤m)是(7)的解。当m=0时,结论仍成立。 我们定义BR(0)是以0为圆心,R为半径的球。 引理1 设{(un,vn)}在E中有界,则存在(u,v)∈Ε,使得un弱收敛于u,vn弱收敛于v,且满足 证明 令 则 因为un弱收敛于u,vn弱收敛于v,则存在{(un,vn)}的子序列(仍记作{(un,vn)}),对任意的自然数n,存在a(x)∈Lα+β(BR(0)),使得|un(x)|≤a(x),|vn(x)|≤a(x)在BR(0)中几乎处处成立。 由控制收敛定理可知 由Hölder和Sobolev不等式,我们有 定义BR(y)是以y为圆心,R为半径的球。从文献[15,21]中我们引入|ωn|的集中函数: ∀t≥0. 由文献[16,22],我们有以下引理。 引理2 设{ωn}是H1(RN)上的有界序列,且Qn(t0;ωn)→0,t0>0,则在Lp(RΝ)中有ωn→0,2 引理3 任意给定常数C0>0,存在δ>0,使得:如果(u,v)∈E是(11)的解,且满足‖u‖+‖v‖≤C0,|u|2+|v|2≤δ,那么(u,v)≡(0,0)。 证明 命题1的证明 首先,设{(un,vn)}是I关于c∈R的一个(PS)c序列,即: 则对任意的(φ,ψ)∈Ε,有: 即 则 因此我们有 重复上面的过程且发现这个过程可以在有限步后停止,设(ui,vi)是(11)的解,我们有 因此,由引理3可知m不能趋于∞. 则存在一个正常数ρ0,使得Ι(u,v)≥0. 易知h(t)在t0处达到最大且 (12) 定义Bρ0={u,v∈H1(RΝ):‖(u,v)‖<ρ0}. (13) (14) 证明 其中 当t→0时,我们有Ι(u0+tω1,v0+tω2)→Ι(u0,v0)<0. 当t→∞时,我们有Ι(u0+tω1,v0+tω2)→-∞. 易知当0 Ι(u0+tω1,v0+tω2)<Ι(u0,v0)+J∞,∀t∈[0,t1)∪[t2,∞). (15) 要证(14)式,我们只需证明 (16) 对任意的非负实数a,b,c,d满足(a+b)α(c+d)β>aαcβ+bαdβ+αaα-1bcβ+βaαcβ-1d. 因此,我们有: (17) 则由K的定义与(17)式可知,(16)式成立。 由引理5和命题2可知,存在ρ0>0,使得 Ι(u0,v0)≥0,∀(u0,v0)∈Sρ0,Ι(u0,v0)<0,∀(u0,v0)∈Bρ0, 易知存在t0>0,当t≥t0时,使得Ι(u0+tω1,v0+tω2)<0. 设 当m=0时,则c=Ι(u0,v0)<0,矛盾。 当m≥1时,则c=Ι(u0,v0)+J∞,矛盾。



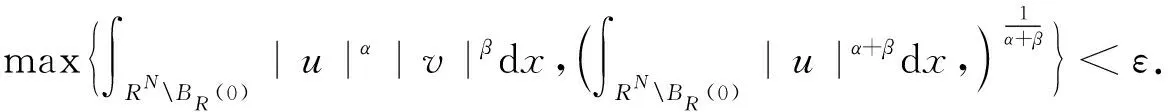








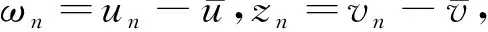




2 局部极小值的存在性



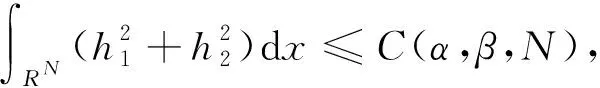






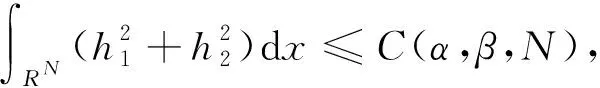

3 定理的证明




