一类非线性分数阶q-导数方程的正解

郭福日,王振芳,罗芳

(山西大同大学 数学与统计学院,山西 大同 037009)

0 引言

近年来,越来越多的研究者专注于分数阶边值问题的研究[1-4],特别是分数阶q-导数边值问题正解存在性的研究[5-10],已经成为一个热点。上述文献研究正解存在性时,利用的方法主要是锥拉伸锥压缩不动点理论、Schauder不动点理论、Leggect-williams不动点理论。文献[11]利用不动点指数理论,讨论了下面非线性分数阶q-导数积分边值问题，

(1)

至少有两个,有三个正解的存在性。就我们所知,研究非线性项带参数的分数阶q-导数积分边值问题,特别是讨论正解依赖于参数的性质的文献不多。受文献[12-15]启发,本文讨论了一类非线性分数阶q-导数积分边值问题

(2)

正解的存在唯一性,并且给出了正解依赖与参数λ的一些性质,其中2<α≤3,0<μ<[α]q,参数λ>0.我们的结果不仅保证对任意参数λ(λ>0)边值问题(2)正解的存在唯一性,而且可以通过构造迭代序列来逼近方程的正解。

注 当λ=1时,方程(2)就退化成方程(1)。

1 准备知识

为了读者方便,下面给出一些必要的定义和引理,定义见文献[5,16]。

定义1 设E是实Banach空间,如果P是E中某非空凸闭集,并且满足下列两个条件:

(1)x∈P,λ≥0⟹λx∈P;

(2)x∈P,-x∈P⟹x=θ,θ表示E中的零元素;则称P是E中的一个锥。

定义2 设P是E中的一个锥,则可在E中的元素间引入半序:x≤y(x,y∈E),如果x-y∈P.

引理1[16]设E是实Banach空间,P是E中的锥,锥P正规的充要条件是:如果存在常数N>0,对任意的x,y∈E,使得当θ≤x≤y时,恒有‖x‖≤N‖y‖(满足此式的最小N称为P的正规常数)。

定义3 设E是实Banach空间,对所有x,y∈E,如果存在λ>0,μ>0使得λx≤y≤μx,则称x,y等价,并用符号x～y表示。 若给定h>θ,定义集合Ph={x∈E|x～h}.

定义4 函数f:[0,1]→R的α阶q-积分(Riemann-Liouville型)为

(3)

函数f的α阶q-导数为

(4)

其中k是大于或等于α的最小整数。

引理2[12]设E为实的Banach空间,P是一个正规锥且P⊂E,h>θ,设A:P→P的增算子,且满足下列条件:(a) 存在h0∈Ph使得Ah0∈Ph;(b) 对任意x∈P,t∈(0,1),存在φ(t)∈(t,1)使得A(tx)≥φ(t)Ax,则有以下结论:

(1)算子方程Ax=x有唯一的解x*∈Ph;

引理3[12]在满足引理2的条件下,假设xλ(λ>0)是算子方程Ax=λx唯一的解,则有以下结论:

(1)xλ关于λ严格递减,即当0<λ1<λ2时,有xλ1>xλ2;

(2)如果存在γ∈(0,1)使得φ(t)≥tγ,t∈(0,1),则xλ关于λ连续,即当λ→λ0(λ0>0)时,有‖xλ-xλ0‖→0;

引理4[11]设2<α≤3,0<μ<[α]q,x∈C1[0,1],则下列边值问题

(5)

(6)

引理5[11]由(6)所定义的格林函数G(t,qs)有下面的性质:

(1)G(t,qs)是连续函数,并且G(t,qs)≥0,t,s∈[0,1];

(2)

(7)

其中M0=max{[α-1]q([α]q-μ)+μqα,qα-1[α]q}.

2 主要结果及证明

令E=C[0,1],定义范数‖x‖=max{|x(t)|:t∈[0,1]}.取锥

P={x∈C[0,1]|x(t)≥0,t∈[0,1]} .

(8)

显然锥P为正规锥,正规常数为1。

定理1 假设:

(H1)函数f:[0,1]×[0,+∞)→[0,+∞)的连续函数,并且f(t,0)≢0;

(H2)对于每一个t∈[0,1],f(t,x)关于x单调递增;

(H3)对任意r∈(0,1),存在φ(r)∈(r,1)使得

f(t,rx)≥φ(r)f(t,x),t∈[0,1],x∈[0,+∞),

那么有以下结论成立:

(9)

证明 对于任意u∈P,定义算子

(10)

由引理4可知,u(t)是边值问题(2)的解当且仅当u(t)=λAu(t),因为f(t,x)≥0,G(t,qs)≥0,显然A:P→P. 由(H1)-(H2)可知,算子A递增。

下面证明A满足引理2的所有条件。由(H3)可知

φ(r)Au(t),t∈[0,1].

(11)

因此对任意u∈P,r∈(0,1),有A(ru)≥φ(r)Au.

令h0=h,我们证明Ah∈Ph.由(H2)和格林函数的性质可知

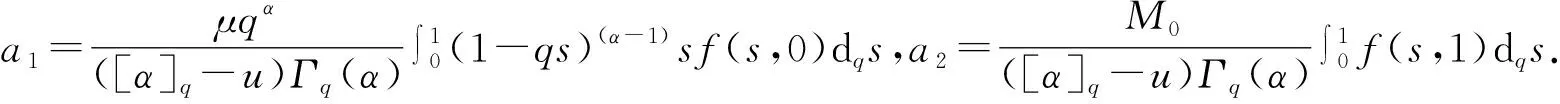
由于f(t,0)≢0,0

即a1h≤Ah≤a2h,则Ah∈Ph.

(12)

特别地,定理1中当λ=1时可以得到以下推论。

推论1 假设(H1)-(H3)成立,那么下列分数阶q-导数边值问题

(13)