Normality Criteria of Zero-free Meromorphic Functions
XIE Jia, DENG Bing-mao
(1School of Mathematics and Information Science, Guangzhou University, Guangzhou, Guangdong,510006, P.R. China; 2School of Financial Mathematics and Statistics, Guangdong University of Finance, Guangzhou, Guangdong, 510521, P.R. China)
Abstract: Let k be a positive integer, let h(z)0 be a holomorphic functions in a domain D, and let F be a family of zero-free meromorphic functions in D, all of whose poles have order at least l. If, for each f ∈F, P(f)(z)−h(z) has at most k +l −1 distinct zeros(ignoring multiplicity) in D, where P(f)(z)=f(k)(z)+a1(z)f(k−1)(z)+···+ak(z)f(z) is a differential polynomial of f and aj(z)(j =1,2,··· ,k) are holomorphic functions in D, then F is normal in D.
Key words: Meromorphic Function; Normality; Zero-free
§1. Introduction and Main Result
Let D be a domain in C and F a family of meromorphic functions in D. F is said to be normal in D (in the sense of Montel) if each sequence {fn} ⊂F has a subsequence {fnj}which converges locally uniformly in D with respect to the spherical metric, to a meromorphic function or ∞.
We define that P(f)(z) is a differential polynomial of f, where P(f)(z) = f(k)(z) +a1(z)f(k−1)(z)+···+ak(z)f(z) and aj(z)(j =1,2,··· ,k) are holomorphic functions in D.
In 1959, Hayman[4]proved the following result.
Theorem ALet f be a nonconstant meromorphic function in C and k be a positive integer. Then f or f(k)−1 has at least a zero. Moreover, if f is transcendental, then f or f(k)−1 has infinitely many zeros.
The normality corresponding to Theorem A was conjectured by Hayman[5]and confirmed by Gu[3]in 1979.
Theorem BLet F be a family of zero-free meromorphic functions in a domain D and k be a positive integer. If f(k)1 for each f ∈F, then F is normal in D.
In 1986, Yang[9]extended Theorem B as follows.
Theorem CLet F be a family of zero-free meromorphic functions in a domain D and h(0) be a holomorphic function in D. If, for each f ∈F, f0 and f(k)h for z ∈D, then F is normal in D.
Chang[1]improved Theorem B and proved the following result.
Theorem DLet F be a family of zero-free meromorphic functions in a domain D and k be a positive integer. If, for each f ∈F, the function f(k)−1 has at most k distinct zeros(ignoring multiplicity) in D, then F is normal in D.
Deng, Fang and Liu[2]extended Theorem C and proved the following result.
Theorem ELet F be a family of zero-free meromorphic functions in a domain D, let h(0) be a holomorphic function in D, and let k be a positive integer. If, for each f ∈F,f(k)−h has at most k distinct zeros (ignoring multiplicity) in D, then F is normal in D.
In 2013, Liu, Deng and Yang[6]replaced f(k)(z)−h(z) by P(f)(z)−h(z), and proved the following result.
Theorem FLet F be a family of zero-free meromorphic functions in a domain D, let h(0) be a holomorphic function in D, and let k be a positive integer. If, for each f ∈F,P(f)(z)−h(z) has at most k distinct zeros (ignoring multiplicity) in D, then F is normal in D.
In this paper, we consider about the order of poles of f. Here is our main result.
Theorem 1Let k be a positive integer,let h(0)be a holomorphic functions in a domain D,and let F be a family of zero-free meromorphic functions in D,all of whose poles have order at least l. If, for each f ∈F, the function P(f)(z)−h(z) has at most k+l −1 distinct zeros(ignoring multiplicity) in the domain D, then F is normal in D.
ExampleSuppose that F ={fn(z)=1/nzl:n ≥(k+l−1)!+1},that P(fn)(z)=that D = {z : |z| < 1} and that h(z) = 1/(z −1)k+l, where k is a positive integer. Then, for each fn∈F, the function P(fn)(z)−h(z) has k+l distinct zeros (ignoring multiplicity) in D,but F is not normal in D. This shows that the condition in Theorem 1 that P(f)−h has at most k+l −1 distinct zeros (ignoring multiplicity) in D is best possible.
Corollary 1Let F be a family of zero-free meromorphic functions in a domain D, let h(0) be a holomorphic functions in D, and let k be a positive integer. If, for each f ∈F,all of whose poles have order at least l, and the function f(k)(z)−h(z) has at most k+l −1 distinct zeros (ignoring multiplicity) in D, then F is normal in D.
Corollary 2Let F be a family of zero-free meromorphic functions in a domain D, and k be a positive integer. If, for each f ∈F, all of whose poles have order at least l, and the function f(k)has at most k+l −1 fixed points (ignoring multiplicity) in D, then F is normal in D.
§2. Some Lemmas
Lemma 1[7]Let α ∈R satisfying −1 < α < ∞and let F be a family of zero-free meromorphic functions in a domain D. If F is not normal at z0∈D,then there exist points zj(∈D)→z0, functions fj∈F, and positive numbers ρj→0+, such that gj(ξ)=f(zj+ρjξ)converges locally spherically uniformly in C to a nonconstant zero-free meromorphic function g(ξ).
Lemma 2[8]Let f be a transcendental meromorphic function,let a(0)be a polynomial,and let k be a positive integer. If f0, then f(k)−a has infinitely many zeros.
Lemma 3Let f be a nonconstant zero-free rational function,all of whose poles have order at least l, let a(0) be a polynomial and let k be a positive integer. Then f(k)−a has at least k+l distinct zeros (ignoring multiplicity) in C.
ProofSuppose that

since f is a nonconstant zero-free rational function, f is not a polynomial, and hence has at least one finite pole with order at least l. Further, by calculation, the function f(k)−a has at least one zero in C. Thus, we can write
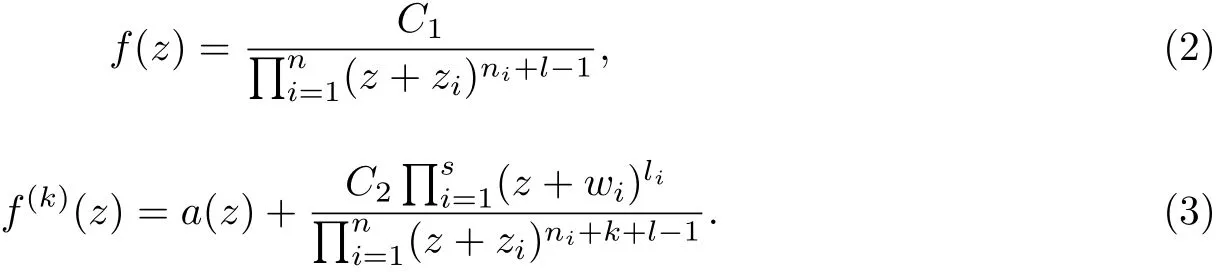
Where C1and C2are nonzero constants, m, n, s, li, mi, and ni≥1(1 ≤i ≤n) are positive integers, the vi(when 1 ≤i ≤m) are distinct complex numbers, and the zi(when 1 ≤i ≤n)and wi(when 1 ≤i ≤s) are distinct complex numbers. Set
Then by induction, we deduce from (2) that

where Pkis a polynomial of deg Pk=(n −1)k. Thus, by (1), (3), and (4),
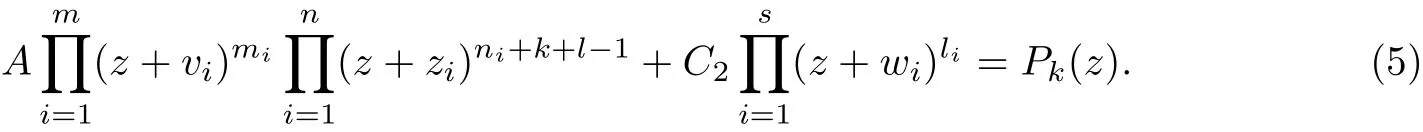

and C2=−A. Thus by (5), we get

where Q(t)=t(n−1)kPk(1/t)/A is a polynomial of deg Q ≤(n −1)k, and it follows that

Logarithmic differentiation of (6) shows that

We consider two cases.
Case 1If deg a=M =0then a is constant. Thus (7) may be rewritten:

Comparing the coefficients of tj(j =0,1,··· ,N +k+n(l −1)−2), we deduce that
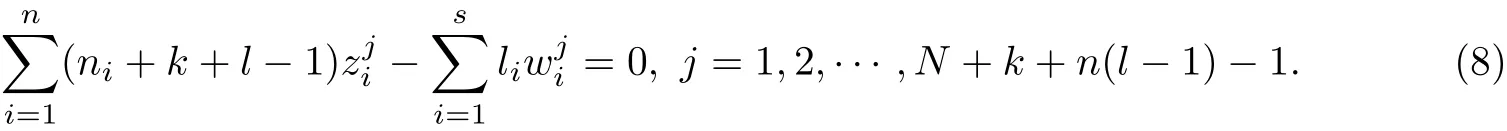
Let zn+i=wi(1 ≤i ≤s).
Subcase 1.10 for each i ∈{1,··· ,n+s}. Noting that0 and using (8), we deduce that the system of linear equations

has a nonzero solution
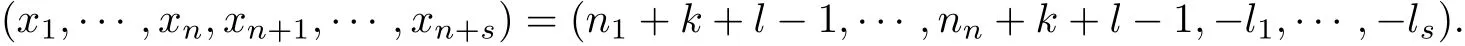
If n+s ≤N +k+n(l −1), then by Cramers rule,

where 0 ≤j ≤N+k+n(l −1)−1. However, the determinant is a Vandermonde determinant,so cannot be 0, which is a contradiction. Hence, we conclude that n+s>N +k+n(l −1). It follows from this and the inequality N =≥n that s ≥k+l.
Subcase 1.2There exist i ∈{1,··· ,n+s} such that zi= 0, for all. Without loss of generality, we assume that zn+s=0, then it follows from (8) that

has a nonzero solution. Next, using the same argument as in Subcase 1.1, we deduce that s ≥k+l.
Case 2deg a=M ≥1. Comparing the coefficients of tj(j =0,1,··· ,M+N+k+n(l −1)−2) in (7), we deduce that

Set

Obviously, S2∩S3=∅.
Subcase 2.1S1∩S2=and S1∩S3=. Let zn+1= vi(1 ≤i ≤m), and zn+m+i=wi(1 ≤i ≤s).
Subsubcase 2.1.10 for all i ∈{1,...,n+m+s}. Since

it follows from (9) that

has a nonzero solution. Then using the same argument as Subcase 1.1,we deduce that s ≥k+l.
Subsubcase 2.1.2There exist i ∈{1,··· ,n+m+s} such that zi=0, for all. Without loss of generality, we assume that zn+m+s=0, then it follows from (9) that

has a nonzero solution. Next,using the same argument as Subcase 1.2,we deduce that s ≥k+l.
Subcase 2.2S1∩S2= ∅and S1∩S3= ∅. Without loss of generality, we may assume that S1∩S2={v1,v2,··· ,vM1}, where vi=zi(1 ≤i ≤M1). Let M3=m −M1, and set
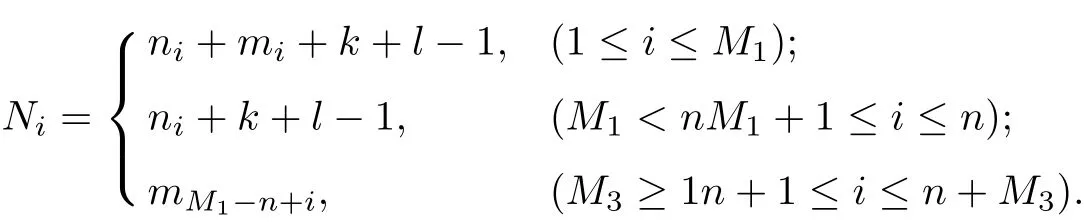
If M3≥1, then set zn+i=vM1+i(1 ≤i ≤M3). In the subcase, (9) may be rewritten:
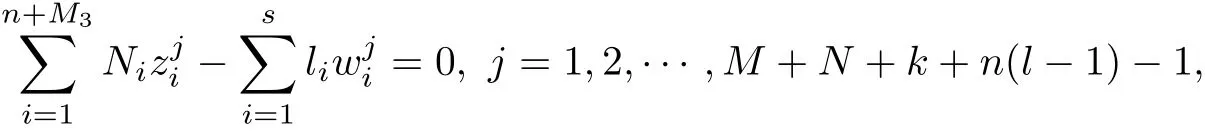
where 0 ≤M3≤m −1. Using the argument of Subcase 2.1, we deduce that s ≥k+l.
Subcase 2.3S1∩S2= ∅and S1∩S3∅. Without loss of generality, we may assume that S1∩S3={v1,v2,··· ,vM2}, where vi=wi(1 ≤i ≤M2). Let M4=m −M2, and set

If M4≥1, then set ws+i=vM2+i(1 ≤i ≤M4). In the subcase, (9) may be rewritten that

where 0 ≤M4≤m −1. Using the argument of Subcase 2.1, we deduce that s ≥k+l.
Subcase 2.4S1∩and S1∩S3Without loss of generality, we may assume that S1∩S2= {v1,v2,··· ,vM1}, S1∩S3= {w1,w2,··· ,wM2}, where vi= zi(1 ≤i ≤M1)and wi=vM1+i(1 ≤i ≤M2). Set M5=m −M2−M1, and set

If M5≥1, then set zn+i=vM1+M2+i(1 ≤i ≤M5). In the subcase, (9) may be rewritten that

where 0 ≤M5≤m −2. Using the argument of Subcase 2.1, we deduce that s ≥k+l.
This completes the proof of Lemma 3.
§3. Proof of Theorem 1
At first we show that F is normal in the set D= {z ∈D : h(z). Suppose that F is not normal at z0∈D. We may assume that D =∆and h(z0)=1. By Lemma 1, there exist fn∈F, zn→z0and ρn→0+such that gn(ξ)=+ρnξ) converges locally spherically uniformly in C to a nonconstant zero-free meromorphic function g(ξ), all of whose poles have order at least l.
We claim that g(k)−1 has at most k+l −1 distinct zeros. Suppose that g(k)−1 has k+l distinct zeros ξj(1 ≤j ≤k+l). Obviously, we have1. Then by


uniformly in compact subsets of C disjoint from the poles of g. And by Hurwitzs theorem, for n sufficiently large, there exist points ξn,j→ξj(j = 1,2,··· ,k +l) , such that P(f)(zn+ρnξn,j) = h(zn+ρnξn,j). However, P(f)(z)−h(z) has at most k+l −1 distinct zeros in D and zn+ρnξn,j→z0, which is a contradiction, and proves our claim.
However, by Lemma 2, we know that g is a rational function. But this contradicts Lemma 3. This contradiction shows that F is normal in.
We now prove that F is normal at{z :h(z)=0}. Making standard normalizations,we may assume that h(z)=zmb(z) (z ∈∆), where m ≥1, b(0)=1 and h(z)0 for 0<|z|<1. Let

Suppose not. Then by Lemma 1, there exist Fn∈F∞, zn→0 and ρn→0+such that gn(ξ)=ρ−knFn(zn+ρnξ)converges locally spherically uniformly in C to a nonconstant zero-free meromorphic function g(ξ).
Next we distinguish two cases.
Case 1There is a subsequence of zn/ρn, we still denote as zn/ρn, such that zn/ρn→α,where α is a finite complex number. Let ˜g(ξ)=g(ξ −α), then uniformly in compact subsets of C disjoint from the poles oObviously,0, and the pole of ˜g at ξ =0 has order at least m. Now


uniformly in compact subsets of C disjoint from the polesand all of the poles of G have multiplicity at least l. Since ˜g has a pole of order at least m at ξ = 0, then G(0)0, and noting that
For

uniformly in compact subsets of C. And

That is

So

uniformly in compact subsets of C disjoint from the poles of G.
Since P(f)(z)−h(z) has at most k+l −1 distinct zeros in D, as discussed as the above,we get that G(k)(ξ)−ξmhas at most k+l −1 distinct zeros in C. However, by Lemma 2 and Lemma 3, G(ξ)≡C, where C is a constant. Then we have Gn(ξ)=fn(ρnξ)C, and
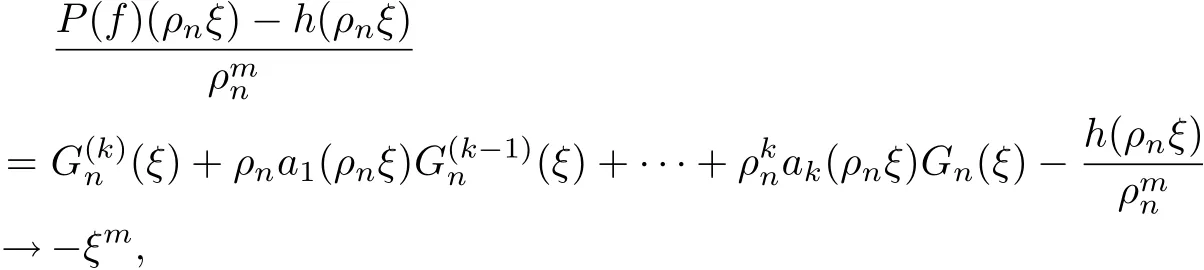
uniformly in compact subsets of C disjoint from the poles of G.
Recall {fn} is normal in, but not normal at z = 0, and since, we can deduce that there exist εn→0, such that fn(εn) = ∞, where |εn| = min{|f−1n(∞)|}. We claim that εn/ρn→∞. Otherwise, suppose that εn/ρn→α. Then

A contradiction. Then εn/ρn→∞.

It is easy to get that P∗(Qn)(z)−zmb(εnz)has at most k+l −1 distinct zeros in C. Obviously,Qn(0. It follows from the above that {Qn} is normal inSince Qnis holomorphic in ∆, and0, by the Maximum Principle Theorem, it is easy to obtain that {Qn} is normal in ∆, then {Qn} is normal in C.
Next, there exist a subsequence of Qn, we still denote as Qn, such that Qn(z) converges locally spherically uniformly in C to a meromorphic function Q(z) or ∞. Since Qn0 and Qn(0) = Gn(0)(ρn/εn)k+m→0, we get Q(z)0 by Hurwitzs theorem. But Qn(1) = ∞, so Q(1)=∞, a contradiction.
Case 2 There exist a subsequence of zn/ρn, we still denote as zn/ρn, such that zn/ρn→∞. By simple calculation,

where


Note that all of the poles of gnhave order at least l at the point zn+that is ξ−zn/ρn, and zn/ρn→∞. By gnconverging locally spherically uniformly in C to g, we see that all of the poles of g have multiplicity at least l. So we have

Note that

disjoint from the poles of g(ξ) and

So

uniformly in compact subsets of C disjoint from the poles of g.
Thus,we proved that F∞is normal at z =0. It remains to prove that F is normal at z =0.Since F∞is normal at z =0 and F(0)=∞for each , F ∈F∞there exist 0<δ <1 such that|F(z)|≥1 for each F ∈F∞and each z ∈∆(0,δ). And0, hence 1/f is analytic in ∆(0,δ)for all f ∈F. Therefore, for all f ∈F, we have
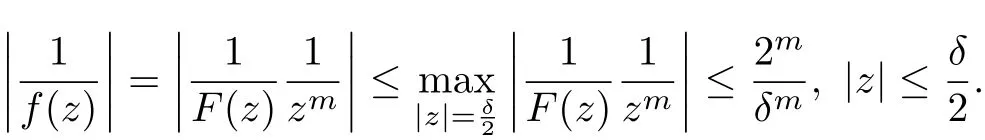
By the Maximum Principle and Montels Theorem, F is normal at z =0. Thus F is normal in D.
This completes the proof of Theorem 1.
 Chinese Quarterly Journal of Mathematics2019年3期
Chinese Quarterly Journal of Mathematics2019年3期
- Chinese Quarterly Journal of Mathematics的其它文章
- On Uniqueness Problem of Meromorphic Functions Sharing Values with Their q-shifts
- Algorithm on the Optimal Vertex-Distinguishing Total Coloring of mC9
- Finite Difference Methods for the Time Fractional Advection-diffusion Equation
- Globally Bounded Solutions in A Chemotaxis Model of Quasilinear Parabolic Type
- Triple Positive Solutions for a Third-order Three-point Boundary Value Problem
- Fixed-time Consensus for Leader-follower Second-order Multi-agent Systems
