On the Solution of Fermat-type Differential-difference Equations
LIU Dan, DENG Bing-mao, YANG De-gui
(Institute of Applied Mathematics, South China Agricultural University, Guangzhou, 510642, P.R.China)
Abstract: In this paper, we mainly discuss entire solutions of finite order of the following Fermat type differential-difference equationand the systems of differential-difference equations of the fromOur results can be proved to be the sufficient and necessary solutions to both equation and systems of equations.
Key words: Fermat-type equation; Differential-difference equation; Entire function
§1. Introduction and Main Results
Let C denote the complex plane and f a meromorphic function on C. In this paper, we assume that the reader is familiar with the fundamental results and the standard notations of the Nevanlinna value distribution theory, see ([9, 13-14]). In addition, S(r,f) = o(T(r,f)), as r →∞outside of a possible exceptional set of finite logarithmic measure,ρ(f)denote the order of growth of f, and S(r,f) denote the set of the small functions of f.
For a meromorphic function f(z), we define its shift by fc(z) = f(z+c) and its difference operators by

In 1966, F. Gross studied the Fermat type functional equation (1.1), and many famous results have been obtained since then, see ([6-7, 12]).

In 2004, Yang et al.[12] studied a generalized Fermat type functional equation (1.2) and proved the following theorem.
Theorem 1.1Let k be a positive integer, let b0, b1, ··· , bk−1, bk0 be constants and let L(f) =. Then the transcendental meromorphic solution of the following equation


In recent years, researches on the value distribution of meromorphic function concerning differences and shifts have become the focus since Halburd, Korhonen [8])and Chiang, Feng [1]successfully proved the lemma analogue that of the logarithmic derivative. This lemma can also be applied to study the existence or the growth of meromorphic solutions to complex difference equations, and many remarkable results have been obtained, see([1-2, 8]).
Liu, Cao, et al [10] considered the Fermat type differential-difference equation

and obtained the following result.
Theorem 1.2The transcendental entire solutions with finite order of the differentialdifference equation (1.3) must satisfy f(z)=, where c=, n is an integer, and B is a constant
Gao(see[3-5])considered the solutions to the corresponding systems to this Fermat differentialdifference equations.

In this paper, we study the entire solutions of finite order to the following equation and the systems of differential-difference equations of the form (1.5)where k is a positive integer.

Theorem 1.3 Let f(z) be an entire solution of finite order of the differential-difference equation (1.4), then
(1) if f(z) is a transcendental solution to (1.4), then k must be an odd number, and f(z)must be of the following form:

where a,b,d are constants satisfying ak=−2i,eac=−1.
(2) if f(z) is a polynomial solution to (1.4), f(z) must be of the form:

where a,b are constants satisfying ac=±1 for k ≥2; a=and c=for k =1, where P is a constant.
Remark 1.4 Let f(z) be the form of (1.6), then

since k is an odd number and ak=−2i.
And
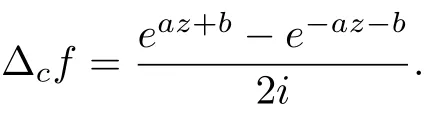
If f(z)is of the form(1.7),it can also be proved that the polynomial(1.7)is the polynomial solution to equation (1.4).
Hence, f(z) of the form (1) and (2) are all the entire solutions of finite order to equation(1.4).
For the systems of differential-difference equations of the from (1.5), we obtained the following result,
Theorem 1.5 Let (f1(z),f2(z)) be an entire solutions with finite order of the systems of differential-difference equation (1.5), then (f1,f2) must be of the following form:
(1) Let (f1,f2) be a pair of transcendental entire solution to equation (1.5), then k must be an odd number, either
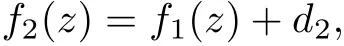
and

where a,b,d1,d2are constants satisfying eac=(−1)k,ak=−2i;
or

and

where a,b,d1,d2are constants satisfying eac=(−1)k,ak=2i.
(2) Let (f1,f2) be a pair of polynomial solution to equation (1.5), then
for k ≥2, f1(z) = a1z+b1,f2(z) = a2z+b2, where a1,a2,b1,b2are constants satisfying a1c=a2c=±1;
for k = 1, f1=+ b1, f2=, whereP,Q,b1,b2,c are constants satisfying c=and e2P−e−2P=e2Q−e−2Q.
Remark 1.6For the case f2(z)=f1(z)+d2when ak=−2i and the case f2(z)=f1(z)+when ak= 2i, it can be proved as same as Remark 1.4 that (f1,f2) are the transcendental entire solution to(1.5). And for the case of polynomial solution,it’s easy to prove that they are also the solution to the equation (1.5). Thus Theorem (1.4) gives all entire solutions of finite order to the equation (1.5).
§2. Some Lemmas
Lemma 2.1[14]Suppose that f1(z),f2(z),··· ,fn(z)(n ≥3) are meromorphic functions which are not constants except for fn(z). Furthermore, let1. If fn(z)0 and

where λ<1 and k =1,2,··· ,n −1, then fn≡1.
Lemma 2.2[14]Suppose that f1(z),f2(z),··· ,fn(z)(n ≥2) are meromorphic functions and g1(z),g2(z),··· ,gn(z) are entire functions satisfying the following conditions:
(2) The orders of fjare less than that of egk−glfor 1 ≤j ≤n,1 ≤k Lemma 2.3[14](Hadamard’s Factorization Theorem)Let f be an entire function of finite order ρ(f) with zeros {z1,z2,···}⊂C{0} and a k-fold zero at the origin. Then where P(z) is the canonical product of f formed with the non-null zeros of f, and Q(z) is a polynomial of degree less than ρ(f). Assume that f(z) is an entire solution with finite order satisfying (1.4). We rewrite () as follows It follows that f(k)(z)+i∆cf(z) and f(k)(z)−i∆cf(z) have no zeros. By Lemma 2.3, we have where P(z) is a polynomial. By (3.2), we get Two cases are considered in the following. Case 1 f is a transcendental entire function.It follows from(3.3)that P(z)is a nonconstant polynomial. Let deg P(z)=m,then m ≥1.By mathematical induction, we can deduce that and where M(z)=(P')k+···+P(k), N(z)=(−1)k(P')k+···−P(k). It follows from (3.4) that By equation (3.3), Combining (3.5) and (3.6), we have then If deg P =m ≥2, it’s obvious that and equation (3.7) satisfies the condition of Lemma 2.1, thus we have which is impossible. Thus deg P =1. Assume that P(z)=az+b, (a0), then By (3.7), we get It follows from equation (3.9) that and Two cases will be discussed depending on the odevity of k. Case 1.1 k is an even number. By equation (3.11), then we have eac=1, hence ak=0, which is a contradiction. Case 1.2 k is an odd number. By equation (3.11), then we have eac=±1. If eac=1, a contradiction will be obtained as same as Case 1.1. If eac=−1, then ak=−2i. It follows from (3.3) that thus where S(z) is a polynomial with deg S ≤k −1. Combining (3.3) and (3.14), we have then ∆cS(z) = 0, which implies that S(z) is a constant. Assume that S(z) ≡d, where d ∈C is a constant. Thus the transcendental entire solution to equation (1.4) is as follows: where ak=−2i,eac=−1 and d ∈C is a constant. Case 2f is a polynomial. It follows from (3.3) that P(z) is a constant. By (3.4), f is a polynomial of degree 1, assume that f(z)=az+b. If k ≥2, by (3.4), eP+e−P=0, then eP=±i. Hence ∆cf =ac=±1. If k =1, by equation (3.3), f(z)=z+b, where b is a constant. Hence by (3.4), Hence we complete the proof of Theorem 1.3. Assume that (f1(z),f2(z)) are entire solutions with finite order satisfying (1.5). We rewrite(1.5) as follows It’s obvious that By Lemma 2.3, we have where P(z), Q(z) are polynomials. By (4.2), we obtain Two cases will be discussed in the following: Case 1 f1is a transcendental entire function. It follows from (4.3) and (4.6) that P(z) and Q(z) are nonconstant polynomials. Assume that deg P(z)=m1, deg Q(z)=m2, and m1,m2≥1. Taking k −th derivative of both sides of equation (4.4), we get where M(z),N(z) are defined as same as those in the proof of Theorem 1.3. Combining (4.4) with (4.5), we have Hence We claim that either Q(z+c)+P(z) or Q(z+c)−P(z) is a constant. Otherwise, suppose both Q(z+c)+P(z) and Q(z+c)−P(z) are non-constant polynomials. Then (4.8) can be written as follows Two subcases will be considered in the following Case 1.1 deg Q=m2≥2. Then and by the assumption We can rewrite equation (4.9) as follows Thus by Lemma 2.1, we get that −iN(z)eQ(z+c)−P(z)≡1, that is eQ(z+c)−P(z)=which contradicts to deg(Q(z+c)−P(z))≥1 . Case 1.2 deg Q=1. Assume that Q(z)=az+b. It’s easy to prove that Thus we can rewrite equation (4.9) as follows It follows from Lemma 2.1 thatwhich contradicts to the fact that eQ(z+c)−P(z)is a transcendental entire function since deg(Q(z +c)−P(z))≥1 . Thus either Q(z+c)+P(z)or Q(z+c)−P(z)is a constant. Without loss of generality,we may assume that Q(z+c)−P(z)≡t, where t is a constant. It’s obvious that deg Q(z)=deg P(z). We claim that deg P = deg Q = 1. Otherwise, suppose that deg P = deg Q = m ≥2, then the coefficient of zmin both P(z) and Q(z) is the same. Hence, We can rewrite equation (4.9) as follows Then by Lemma 2.1, we get thatthat iswhich is impossible since eQ(z+c)−Q(z)is a transcendental entire function as deg(Q(z +c)−Q(z))≥1. Thus deg P = deg Q = 1, we assume that P(z) = az + b1, and Q(z) = az + b2, then M(z)=akand N(z)=(−a)k. Obviously, we have Combining (4.3) and (4.6), (4.4) and (4.5), we have Hence Since e2P(z)and e2Q(z)are transcendental entire functions, by equation (4.11), we have By (4.12) and (4.14), we have then which implies b2=b1+inπ ( n ∈N) is an integer. When eb2−b1=1, by (4.12) and (4.14), we get When k is an even number, then Thus eac=1, then ak=0, which is a contradiction.When k is an odd number, then it can be deduced that eac=±1. If eac=1, then ak=0, a contradiction. If eac=−1, then ak=−2i. Then we can deduce as same as the proof of Theorem 1.3 that where ak=−2i, eac=−1 and b2=b1+i2nπ, n ∈N+. If eb2−b1=−1, (4.12) and (4.14) give the equations, When k is an even number, then Thus eac=1, then ak=0, which is a contradiction. when k is an odd number, then it can be deduced that eac=±1. If eac=1, then ak=0, a contradiction. If eac=−1, then ak=2i. Then we can deduce as same as the proof of Theorem 1.3 that where ak=−2i, eac=−1 and b2=b1+i(2n+1)π, n ∈N. Case 2f1is a polynomial. By (4.3) and (4.6), P(z),Q(z) are two constants, then f2is also a polynomial. By (4.4) and (4.6), it can be deduced that deg f1=deg f2=1. Assume that f1=a1z+b1and f2=a2z+b2, where a1(0),a2(0), b1,b2are constants. If k ≥2, by (4.3) and (4.5), eP+e−P=eQ+e−Q=0, then eP=±i and eQ=±i. Hence by (4.4) and (4.6), If k =1, (4.3) and (4.5) imply that, Then by (4.4) and (4.6), Hence e2P−e−2P=e2Q−e−2Q, and c= Thus Theorem 1.5 is proved completely. AcknowledgementsThe authors would like to thank to anonymous referees for their helpful comments.
§3. Proof of Theorem 1.3








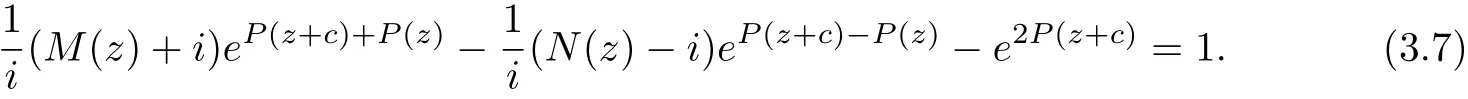















§4. Proof of Theorem 1.5

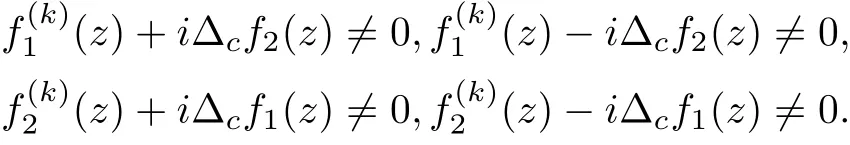


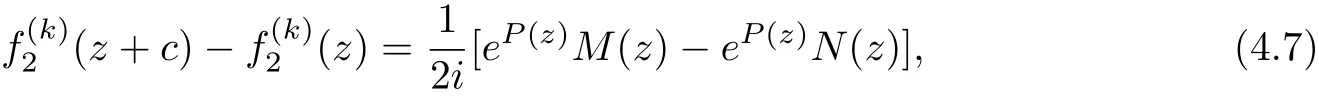





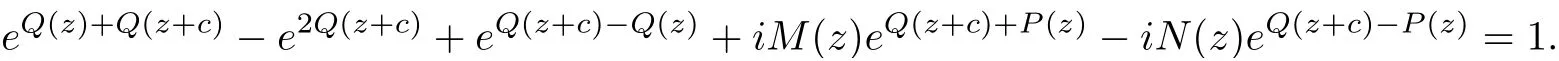
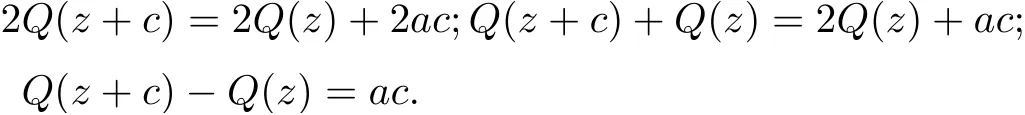











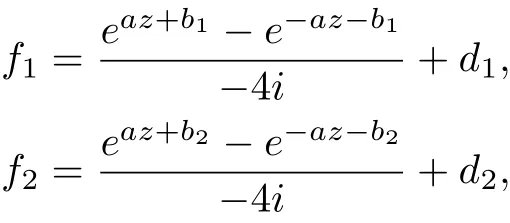
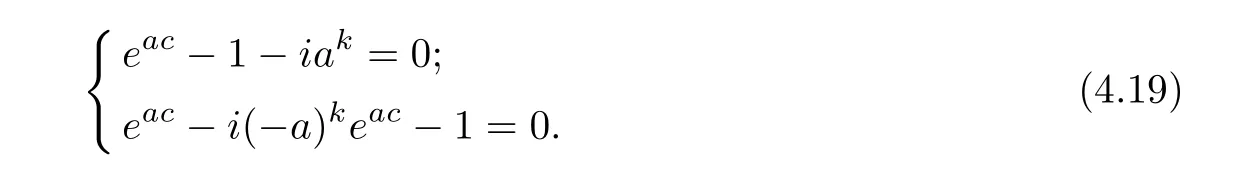


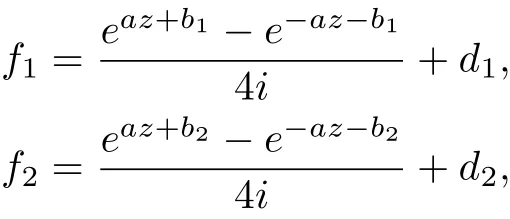
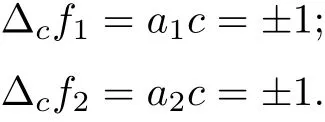
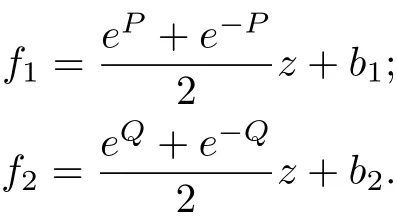
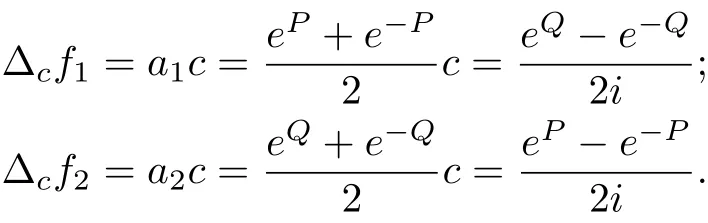
 Chinese Quarterly Journal of Mathematics2019年3期
Chinese Quarterly Journal of Mathematics2019年3期
- Chinese Quarterly Journal of Mathematics的其它文章
- Normality Criteria of Zero-free Meromorphic Functions
- On Uniqueness Problem of Meromorphic Functions Sharing Values with Their q-shifts
- Algorithm on the Optimal Vertex-Distinguishing Total Coloring of mC9
- Finite Difference Methods for the Time Fractional Advection-diffusion Equation
- Globally Bounded Solutions in A Chemotaxis Model of Quasilinear Parabolic Type
- Triple Positive Solutions for a Third-order Three-point Boundary Value Problem
